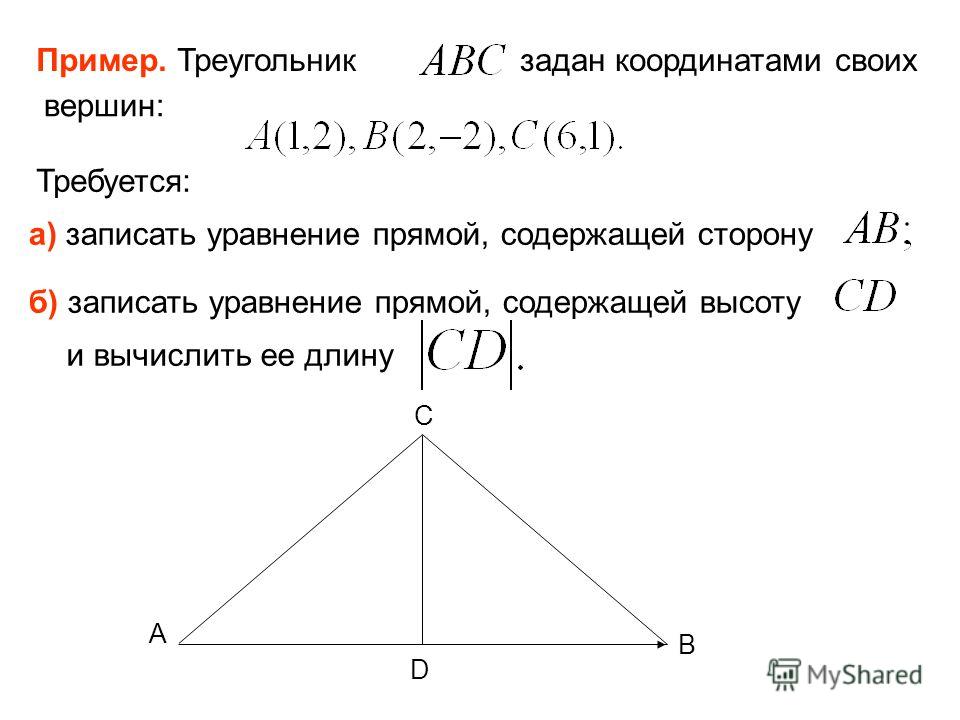
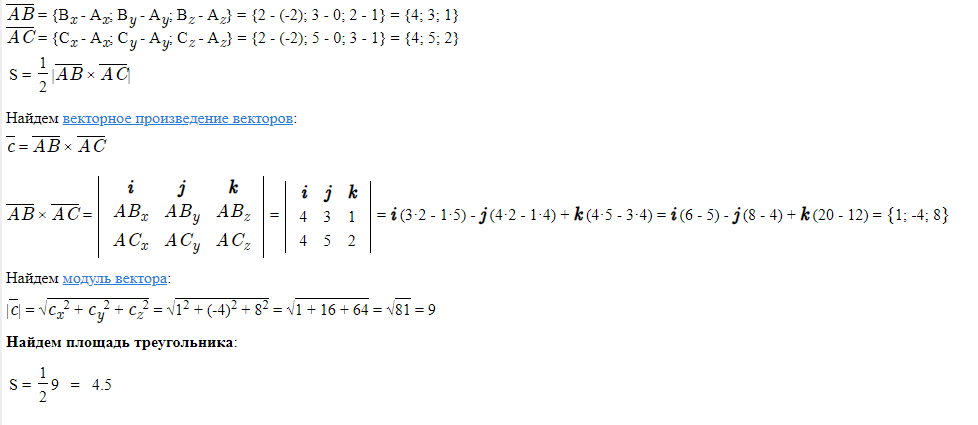Вариант 1 1. В треугольнике АВС стороны ВС=35 см, <В=400, < С=1200. Найдите угол А и стороны АВ, АС. Найдите его площадь и радиус описанной окружности. 2. Вычислить скалярное произведение векторов (-3; -12 ) и (–4; — 3). 3. Вычислить косинус угла между векторами (10; 0) и (9; -8). 4. В параллелограмме АВСД сторона АВ=3 см, АД=4 см, ВД=6 см. Найдите длину диагонали АС. 5. Даны координаты вершин треугольника ABC: A (-6; 1), B (2; 4), С (2; -2). Определите вид треугольника. | Вариант 2 1. В треугольнике АВС стороны ВС=4 см, < В=250, < А=400 Найдите угол С и стороны АВ, АС. Найдите его площадь и радиус описанной окружности. 2.Вычислить скалярное произведение векторов (0; -13) и (1; — 6). 3.Вычислить косинус угла между векторами (24; -8) и (-1; 3). 4.В ромбе АВСД стороны АВ=5 см, ВД=6 см. Найдите длину диагонали АС. 5. Определите вид треугольника KLM, если К(1; 7), L(-2; 4), М(2; 0) | Вариант 1 1. В треугольнике АВС стороны ВС=35 см, <В=400, < С=1200. Найдите угол А и стороны АВ, АС. Найдите его площадь и радиус описанной окружности. 2. Вычислить скалярное произведение векторов (-3; -12 ) и (–4; — 3). 3. Вычислить косинус угла между векторами (10; 0) и (9; -8). 4. В параллелограмме АВСД сторона АВ=3 см, АД=4 см, ВД=6 см. Найдите длину диагонали АС. 5. Даны координаты вершин треугольника ABC: A (-6; 1), B (2; 4), С (2; -2). Определите вид треугольника. | Вариант 2 1. В треугольнике АВС стороны ВС=4 см, < В=250, < А=400 Найдите угол С и стороны АВ, АС. Найдите его площадь и радиус описанной окружности. 2.Вычислить скалярное произведение векторов (0; -13) и (1; — 6). 3.Вычислить косинус угла между векторами (24; -8) и (-1; 3). 4.В ромбе АВСД стороны АВ=5 см, ВД=6 см. Найдите длину диагонали АС. 5. Определите вид треугольника KLM, если К(1; 7), L(-2; 4), М(2; 0) | Вариант 1 1. В треугольнике АВС стороны ВС=35 см, <В=400, < С=1200. Найдите угол А и стороны АВ, АС. Найдите его площадь и радиус описанной окружности. 2. Вычислить скалярное произведение векторов (-3; -12 ) и (–4; — 3). 3. Вычислить косинус угла между векторами (10; 0) и (9; -8). 4. В параллелограмме АВСД сторона АВ=3 см, АД=4 см, ВД=6 см. Найдите длину диагонали АС. 5. Даны координаты вершин треугольника ABC: A (-6; 1), B (2; 4), С (2; -2). Определите вид треугольника. | Вариант 2 1. В треугольнике АВС стороны ВС=4 см, < В=250, < А=400 Найдите угол С и стороны АВ, АС. Найдите его площадь и радиус описанной окружности. 2.Вычислить скалярное произведение векторов (0; -13) и (1; — 6). 3.Вычислить косинус угла между векторами (24; -8) и (-1; 3). 4.В ромбе АВСД стороны АВ=5 см, ВД=6 см. Найдите длину диагонали АС. 5. Определите вид треугольника KLM, если К(1; 7), L(-2; 4), М(2; 0) |
Задачи по геометрии без использования циклов
Təhlili ilə verilmiş məsələlər| 1. | Задана точка с координатами х и у. Определить, в какой координатной четверти она расположена. | Решение | Həlli |
| 2. | Даны действительные числа a и b — стороны прямоугольника. Найти периметр и площадь этого прямоугольника | Решение | Həlli |
| 3. | Даны действительные числа A, B, C. Если можно построить треугольник с такими сторонами, то определить вид треугольника: прямоугольный, остроугольный или тупоугольный | Решение | Həlli |
4. | Заданы координаты трех вершин прямоугольника. Необходимо определить координаты четвертой вершины. | Решение | |
| 5. | Даны 4 точки заданные координатами. Является ли данная фигура трапецией? | Решение | Həlli |
| 6. | Дан радиус R и центр круга (X0,Y0). Найти угол, под которым виден этот круг из начала координат. Начало координат не лежит внутри круга. | Решение | Həlli |
| 7. | Определить лежит ли точка а на прямой y=kx+l. | Решение | Həlli |
| 8. | Два отрезка на плоскости задаются парами координат концевых точек. Определить, пересекаются ли эти отрезки | Решение | Həlli |
| 9. | Найти площадь треугольника (используя формулу Герона). | Решение | Həlli |
| 10. | На плоскости заданы две точки A(x1,y1) и B(x2,y2). Определить, какой из отрезков — OA или OB образует больший угол с осью OX (Точка О – начало координат) | Решение | Həlli |
| 11. | Треугольник на плоскости задается целочисленными координатами вершин. Для заданной точки Z(x,y) определить, принадлежит ли она стороне треугольника или лежит внутри или вне его. | Решение | Həlli |
| 12. | Даны две точки и прямая. Лежат ли точки по одну сторону от прямой или по разные | Решение | Həlli |
| 13. | Даны вершины треугольника. Определить можно ли разместить этот треугольник в круге радиуса | Həlli | |
| 14. | На плоскости даны три точки, не лежащие на одной прямой. Найти радиус окружности, проходящей через эти три точки | Решение | Həlli |
| 15. | Найти площадь сектора круга радиуса r и углом fi. Радиус и угол ввести с клавиатуры. | Решение | Həlli |
| 16. | Даны размеры прямоугольных открытки и конверта. Требуется определить, поместится ли открытка в конверте. | Решение | Həlli |
| 17. | Есть окружность радиуса R с координатами центра x,y и прямая, заданная координатами двух своих точек. Какой длины отрезок прямой лежит внутри окружности? | Решение | Həlli |
| 18. | Задан отрезок с координатами концов x1,y1,x2,y2. В каких координатных четвертях лежит отрезок? Выведите в порядке возрастания номера четвертей, в которых лежит отрезок | Решение | Həlli |
| 19. | Даны координаты 2-х точек. Найти точку на оси Х чтобы сумма расстояний до данных было минимальной | Решение | Həlli |
| 20. | На плоскости расположены две окружности. Необходимо определить количество точек, в которых они пересекаются. | Решение | Həlli |
Задачи для самостоятельного решения
1. Задан круг радиуса R.
Определить, возможно ли в него поместить круги радиусов R1, R2 и R3. Круги не должны пересекаться, но могут касаться друг друга.
2. Дана точка. Лежит ли она в кольце.
3. Дан треугольник с координатами вершин: (X1,Y1), (X2,Y2), (X3,Y3). Найти угол, под которым виден этот треугольник из начала координат. Начало координат не лежит внутри треугольника.
4. Задан прямоугольник со сторонами а, b. Определить, возможно ли в него поместить прямоугольники со сторонами c1, d1 и c2, d2. Прямоугольники не должны пересекаться, но могут касаться друг друга. Стороны всех прямоугольников параллельны осям координат.
5. Определить, пересекается ли прямая y=ax+b и отрезок с концами (x1,y1), (x2,y2).
6. На плоскости расположены окружность и треугольник. Необходимо определить количество точек, в которых они пересекаются.
7. Заданы площадь кольца и радиус внешней окружности. Определить радиус внутренней окружности.
8.
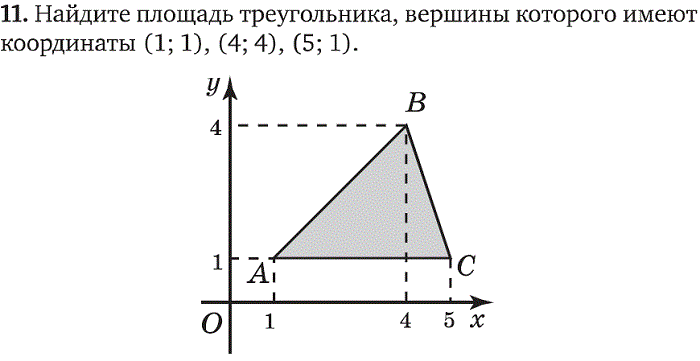На плоскости расположены два треугольника. Необходимо определить количество точек, в которых пересекаются их стороны.
9. Задано 4 числа a, b, c, d, определяющие длины отрезков. Определить, можно ли с этих отрезков образовать параллелограмм
10. Задан круг радиуса R. Определить, возможно ли в него поместить круги радиусов R1 и R2. Круги не должны пересекаться, но могут касаться друг друга.
11. Даны координаты начала и конца диагонали прямоугольника. Найти его площадь.
12. Даны действительные числа A, B, C, D. Определить, можно ли построить четырехугольник с такими сторонами.
13. На плоскости заданы два круга координатами центров и радиусами. Найти площадь их пресечения.
14. Дана окружность (координатами своего центра и радиусом) и прямая (своим уравнением). Требуется найти точки их пересечения (одна, две, либо ни одной).
15. Дана точка. Лежит ли она в прямоугольнике
Треугольники — Part 8
Составить уравнение биссектрисы угла можно с помощью свойства биссектрисы угла.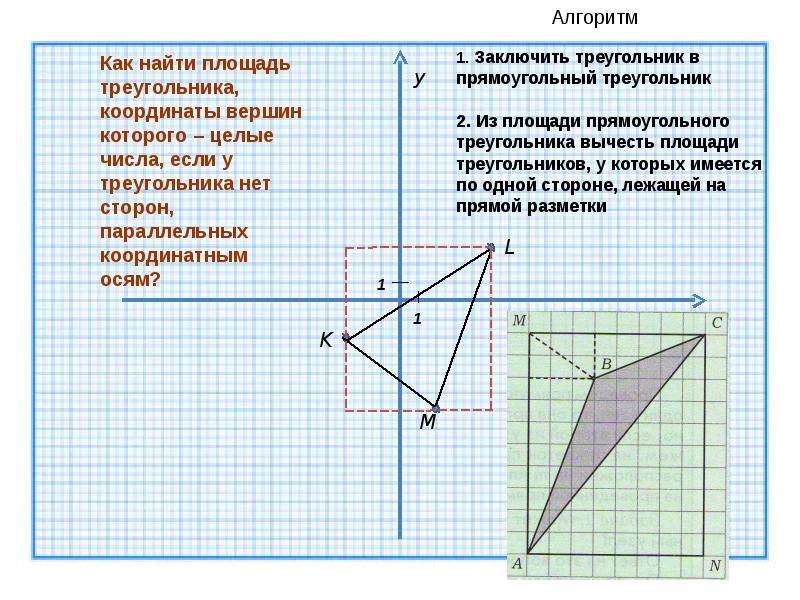
Выведем уравнения биссектрис углов, образованных двумя пересекающимися прямыми a1x+b1y+c1=0 и a2x+b2y+c2=0.
Читать далее
Декартовы координаты на плоскостиКак найти площадь треугольника по координатам его вершин?
1способ:
Найти длины трёх сторон треугольника и вычислить площадь по формуле Герона. Способ удобен, если длины сторон являются целыми числами. В противном случае предстоят громоздкие вычисления.
2 способ:
вывести формулу для нахождения площади и использовать её для вычисления.
Читать далее
Декартовы координаты на плоскостиВ любом треугольнике все три высоты пересекаются в одной точке. Все высоты в остроугольном треугольнике лежат внутри треугольника (как и точка пересечения высот).
Задача.
Высоты BB1 и CC1 остроугольного треугольника ABC пересекаются в точке E.
Доказать, что углы BB1C1 и BCC1 равны; углы B1C1С и BB1C равны.
Читать далее
Рассмотрим, как построить высоту треугольника с помощью чертежного угольника.
Чтобы построить высоту остроугольного треугольника, надо приложить угольник так, чтобы одна сторона прямого угла проходила через вершину треугольника, а вторая — через противоположную этой вершине сторону.
AK⊥BC.
AK — высота треугольника ABC, проведённая из вершины A к противолежащей стороне BC.
Читать далее
Элементы треугольникаКак найти углы параллелограмма, если известен угол между высотой и биссектрисой угла параллелограмма?
Задача 1
Угол между биссектрисой тупого угла параллелограмма и высотой, проведенной из той же вершины, равен α.
Найти углы параллелограмма.
Дано: ABCD — параллелограмм,
BH — высота, BF — биссектриса ∠ABC, ∠HBF=α
Найти: ∠A, ∠ABC, ∠C, ∠D
Читать далее
ПараллелограммМы уже находили косинусы углов треугольника по его сторонам в произвольном треугольнике и косинус острого угла прямоугольного треугольника.
Рассмотрим, как найти косинусы углов треугольника по его вершинам.
Задача
Дано: ΔABC,
A(-2;0), B(6;1), C(-3;-5).
1) Найти косинусы углов треугольника ABC;
2) Определить вид треугольника.
Решение:
Читать далее
Векторы на плоскостиОпределение 1
Скалярным произведением двух векторов называется произведение их модулей на косинус угла между ними.
где
(0°≤φ≤180°).
Если хотя бы один из векторов нулевой, то скалярное произведение принимают равным нулю.
Читать далее
Векторы на плоскостиТеорема Косинусов и Синусов треугольника. Формулы и примеры
Формулировка и доказательство теоремы косинусов
Для начала вспомним теорему Пифагора: в прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов.
Формула Теоремы Пифагора:
a2> + b2> = c2>, где a, b — катеты, с — гипотенуза.
Из формулы следует: a2 = c2 — b2
К полученному выражению прибавим и отнимем квадрат второго катета:
Но так как b = c * cos α, то
Эту формулу мы получили для катетов в прямоугольном треугольнике, но аналогичная связь между стороной а и косинусом противолежащего угла справедлива и для произвольного треугольника.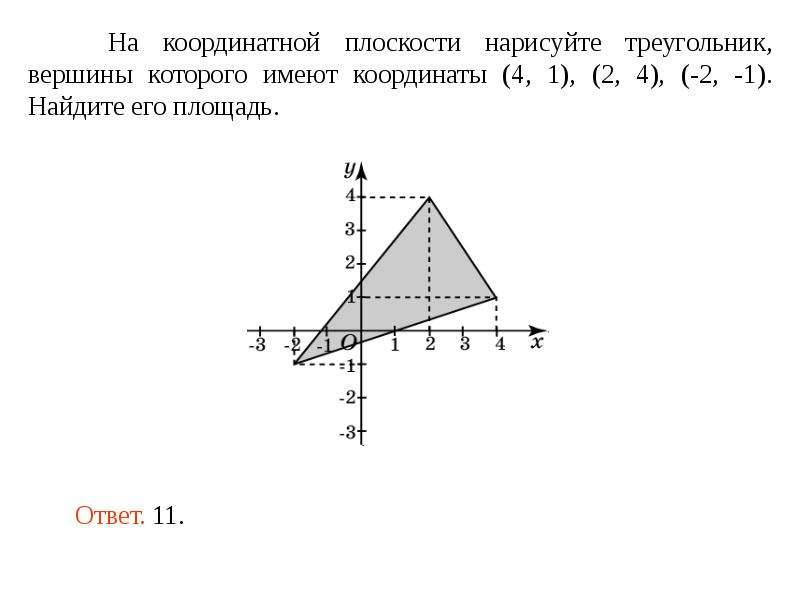
Теорема косинусов звучит так: квадрат стороны треугольника равен сумме квадратов двух других его сторон минус удвоенное произведение этих сторон на косинус угла между ними. |
Формула теоремы косинусов:
a2 = b2 + c2 — 2bc cos α
В доказательстве теоремы косинусов используем формулу длины отрезка в координатах. Рассмотрим данную формулу:
BC2 = (x2 — x1)2 + (y2 — y1)2
В доказательстве теоремы косинусов BC — это сторона треугольника АВС, которая обозначена буквой а. Введем удобную систему координат и найдем координаты нужных нам точек. У точки В координаты (с; 0).
Координаты точки С — (b cos α; b sin α) при α ∈ (0° ; 180°).
BC2 = a2 = (b cos α — c)2 + b2sin2α = b2cos2α + b2sin2α — 2bc cos α + c2 = b2(cos2α + sin2α) — 2bc cos α + c2
cos2α + sin2α = 1 — основное тригонометрическое тождество.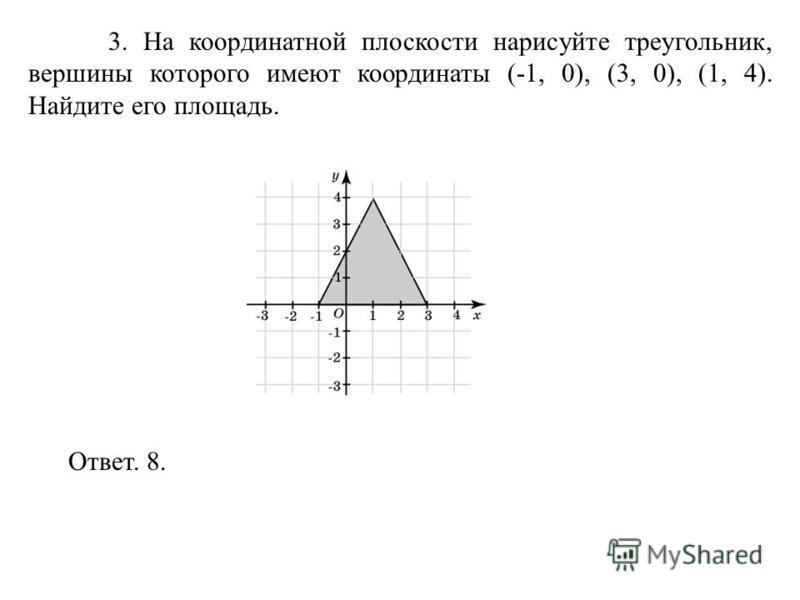
b2(cos2α + sin2α) — 2bc cos α + c2 = b2 + c2 — 2bc cos α
Что и требовалось доказать.
Следствие из теоремы косинусов: теорему косинусов также можно использовать для определения косинуса угла треугольника:
- Когда b2 + c2 — a2 > 0, угол α будет острым.
- Когда b2 + c2 — a2 = 0, угол α будет прямым.
- Когда b2 + c2 — a2 < 0, угол α будет тупым.
Запоминаем
Когда угол α прямой, то теорема косинусов превращаеся в теорему Пифагора.
Сформулируем еще одно доказательство теоремы косинусов.
Пусть нам дан треугольник ABC, в котором из вершины C на сторону AB опустили высоту CD. Это значит:
- AD = b * cos α,
- DB = c – b * cos α.
Запишем теорему Пифагора для двух прямоугольных треугольников ADC и BDC:
- h2 = b2 — (b * cos α)2
- h2 = a2 — (c – b * cos α)2
Приравниваем правые части уравнений:
- b2 — (b * cos α)2 = a2 — (c — b * cos α)2
либо
- a2 = b2 + c2 — 2bc * cos α
Если один из углов при основании тупой (высота упирается в продолжение основания), полностью аналогичен рассмотренному выше.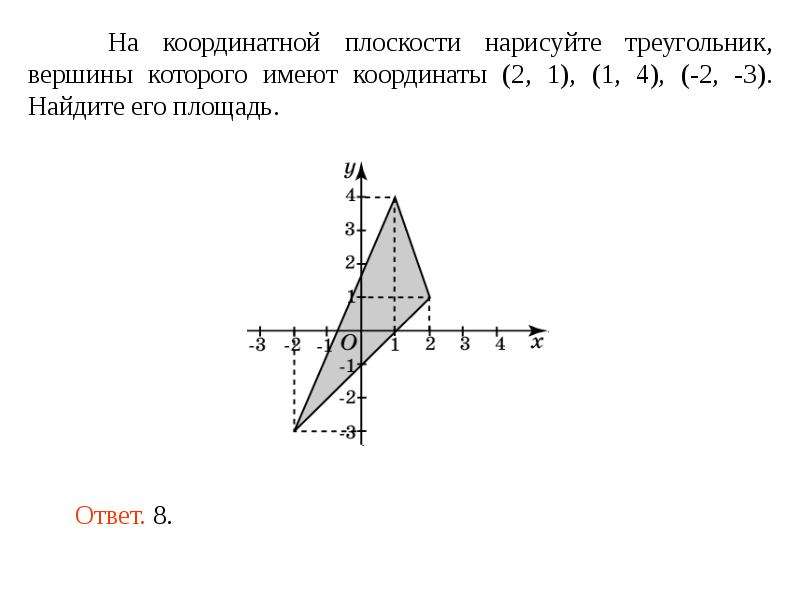
Определим стороны b и c:
- b2 = a2 + c2 — 2ac * cos β;
- c2 = a2 + b2 — 2ab * cos γ.
Формулировка теоремы для каждой из сторон треугольника
Теорема косинусов справедлива для всех сторон треугольника, то есть:
a2 = b2 + c2 — 2bc cos α
b2 = c2 + a2 — 2ca cos β
c2 = a2 + b2 — 2ab cos γ
Таким образом, теорема косинусов обобщает теорему Пифагора. Закон косинуса может быть использован для любого вида треугольника.
Описание формулы косинуса угла из теоремы косинусов
Теорема косинусов позволяет найти как косинус, так и угол треугольника. Найдём косинусы углов:
Аналогично:
Определение угла с помощью косинуса
А теперь обратим внимание на углы.
Как мы уже знаем, косинус угла из промежутка (0°; 180°) определяет угол (в отличие от его синуса).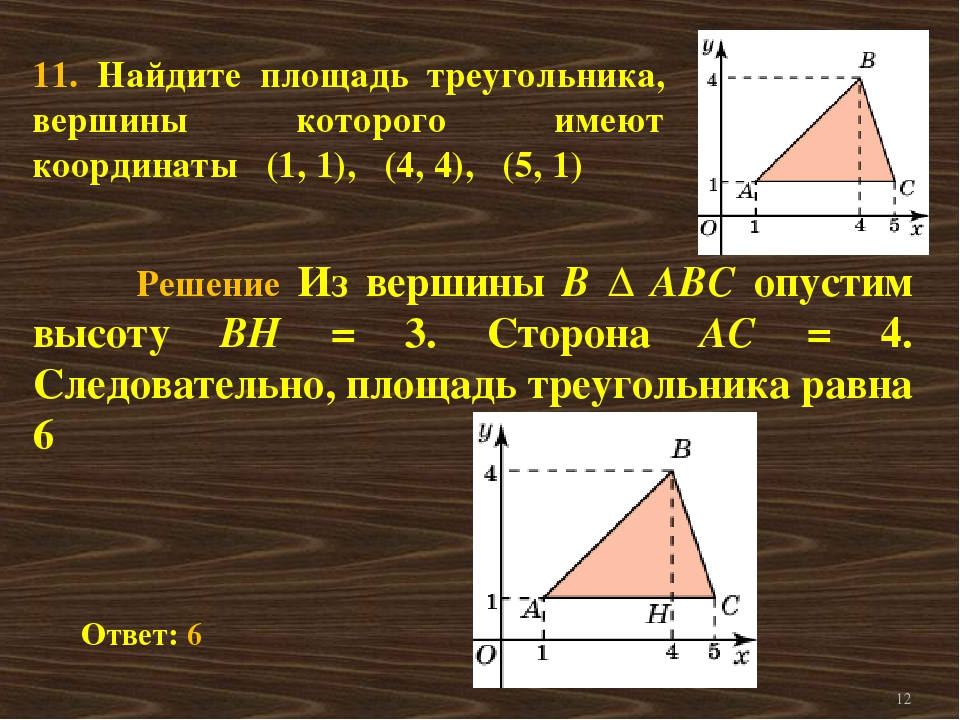
Пусть нам дана единичная полуокружность. Если нам задан cos α, то нам задана точка на верхней полуокружности и задан угол α. Следовательно, cos α однозначно определяет точку М(cos α; sin α), и однозначно определяется угол ∠AOM.
Рассмотрение пределов изменения cos α и sin α
Рассмотрим пределы изменения синуса и косинуса α. Вспомним, что если α — угол треугольника, то он лежит в пределах от 0° до 180°.
Предел изменения косинуса: -1 < cos α < 1.
Предел изменения синуса: 0 < sin α ≤ 1.
- Если cos α > 0, то α ∈ (0°;90°)
- Если cos α < 0, то α ∈ (90°;180°)
- Если cos α = 0, то α = 90°
Примеры решения задач
При помощи теоремы косинусов можно решать задачки по геометрии. Рассмотрим интересные случаи.
Пример 1. Дан треугольник АВС. Найти длину СМ.
∠C = 90°, АВ = 9, ВС = 3, AM/MB = 1/2, где М — точка на гипотенузе АВ.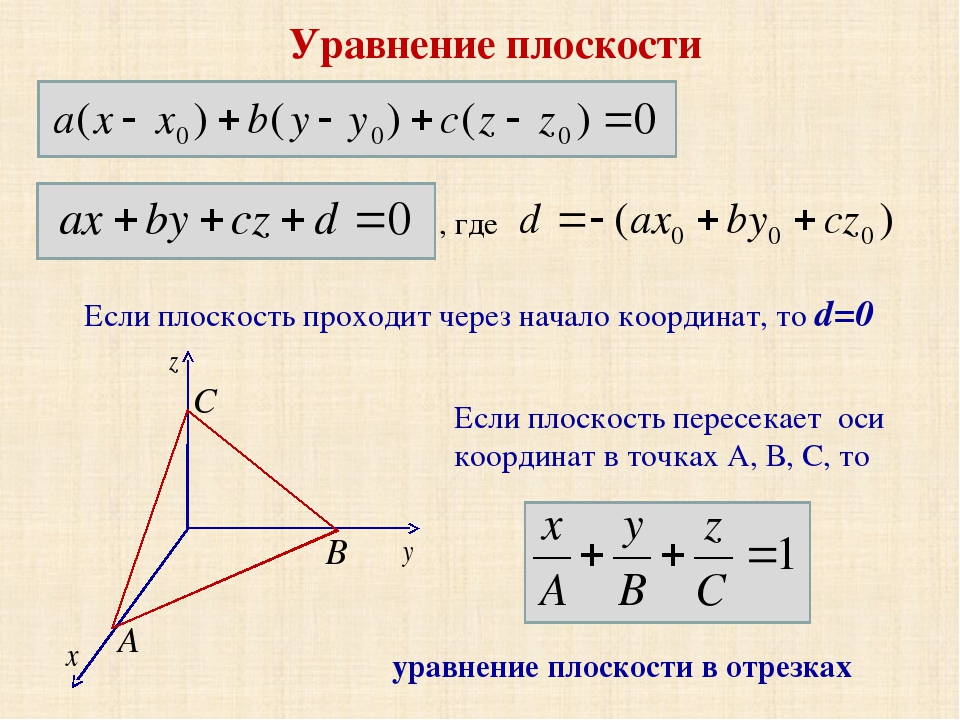
Как решаем:
- Так как АМ + МВ = 9, а AM/MB = 1/2, то АМ = 3, МВ = 6.
Из треугольника АВС найдем cos B: - Из треугольника СМВ по теореме косинусов найдём СМ:
Ответ: СМ = √33.
Пример 2. Дан треугольник АВС, в котором a2 + b2 < c2. Доказать, что ∠C — тупой угол.
Как доказываем:
- Для доказательства нужно вспомнить теорему косинусов для угла ∠C:
- Так как a2 + b2 < c2, то cos C < 0, следовательно, ∠C — тупой.
Что и требовалось доказать.
Эта задача нам показала, что с помощью теоремы косинусов можно определить тупой угол или острый.
- Если c2 = a2 + b2, то ∠C = 90°.
- Если c2 < a2 + b2, то ∠C — острый.
Microsoft Word — геометрия-1.doc
%PDF-1.6 % 955 0 obj > endobj 952 0 obj >stream 2009-08-03T12:57:02ZMicrosoft Word — геометрия-1.doc2009-08-12T12:51:21+04:002009-08-12T12:51:21+04:00application/pdf
Определить существование треугольника по трем сторонам.
Язык PythonУ треугольника сумма любых двух сторон должна быть больше третьей. Иначе две стороны просто «лягут» на третью и треугольника не получится.
Пользователь вводит длины трех сторон. Программа должна определять, может ли существовать треугольник при таких длинах. Это значит, необходимо сравнить суммы всех пар сторон с оставшейся третьей стороной. Чтобы треугольник существовал, сумма всегда должна быть больше отдельной стороны или, по крайней мере, не меньше, если учитывать так называемый вырожденный треугольник.
Поскольку всего три стороны, то можно составить три варианта сложения двух сторон: a + b, b + c, a + c. Первую сумму сравниваем с оставшейся стороной c, вторую — с a и третью — с b. Если хотя бы в одном случае сумма окажется не больше третьей стороны, то делается вывод, что треугольник не существует.
print("Стороны:")
a = float(input("a = "))
b = float(input("b = "))
c = float(input("c = "))
if a + b > c and a + c > b and b + c > a:
print("Треугольник существует")
else:
print("Треугольник не существует")Можно решить задачу сложнее.
Если требуется также определить, какая из сторон больше суммы двух других, то решение может быть таким:
print("Длины сторон треугольника:")
a = float(input("a = "))
b = float(input("b = "))
c = float(input("c = "))
flag = ''
if a + b > c:
if a + c > b:
if b + c > a:
print("Треугольник есть")
else:
flag = 'a'
else:
flag = 'b'
else:
flag = 'c'
if flag != '':
print("Треугольника нет")
print("'%s' > суммы других" % flag)Особого смысла использовать переменную flag здесь нет. Она просто позволяет лишний раз не писать в программе строки, информирующие о том, что треугольник не существует. Большего внимания заслуживает использование вложенных конструкций if-else.
Примерный результат выполнения программы:
Длины сторон треугольника: a = 4 b = 5 c = 10 Треугольника нет 'c' > суммы других
Определить возможность существования треугольника по сторонам
Ниже приведены решения задачи на языке программирования Паскаль двумя способами. В первом случае все стороны проверяются в одном операторе if; во втором случае каждое условие проверяется отдельно, а программа содержит вложенные операторы if-else.
Программа 1 (предпочтительный способ решения):
В языке Паскаль логический оператор and имеет приоритет над операторам >, < и т. п. Поэтому для изменения последовательности выполнения действий в заголовке условного оператора используются скобки.
В условии if проверяется, что каждая из сторон меньше суммы других. Если хотя бы одна будет больше, то все логическое выражение вернет ложь (false). В таком случае сработает ветка else.
var a, b, c: integer;
begin
write (' Длины сторон: ');
readln (a,b,c);
if (a < b+c) and (b < a+c) and (c < a+b) then
writeln ('Треугольник существует.')
else
writeln ('Треугольник не существует.');
readln
end.Программа 2:
В данном случае существование треугольника проверяется по-этапно. Если первое условие возвращает ложь, то программа переходит к последнему else. Если же первое условие соблюдено, то поток выполнения программы оказывается у вложенного if. Здесь проверяется уже второе условие. Если оно возвращает ложь, то программа переходит к предпоследнему else. Если и второе логическое выражение возвращает истину (true), то программа идет к третьему условию. При его соблюдении выполняется тело самого вложенного оператора if. При его несоблюдении сработает самое вложенное else.
Несмотря на то, что данная программа кажется длиннее, в определенных ситуациях она может выполняться быстрее, чем первая. Здесь если внешнее if возвращает ложь, то остальные логические выражения вообще не проверяются. В первой программе могут и проверяться (это зависит от особенностей языка программирования).
var a, b, c: integer;
begin
write ('Длины сторон: ');
readln (a,b,c);
if a < b+c then
if b < a+c then
if c < a+b then
writeln ('Треугольник существует.')
else
writeln ('Треугольник не существует.')
else
writeln ('Треугольник не существует.')
else
writeln ('Треугольник не существует.');
readln
end.Теорема Пифагора (стр. 2 из 2)
«Вершины» — модное слово для «углов», так что это просит меня выяснить, точки — это три угла прямоугольного треугольника. Из быстрого графика Я вижу, что точки — это углы какого-то треугольника типа : Я могу использовать расстояние Формула для определения длин каждой из сторон треугольника, эти длины представляют собой расстояния между парами точек.потом Я могу добавить эти расстояния в теорему, чтобы увидеть, — прямоугольный треугольник. Думаю баллы (2, 3) и (5, 2) отметить гипотенузу, полагая этот треугольник оказывается правильным, поэтому я проверю расстояния, которые путь первый. (2, 3) и (2, 1): (2, 1) и (5, 2): (2, 3) и (5, 2): проверка теоремы (используя квадраты
расстояний): Поскольку квадраты двух меньших расстояния равны квадрату наибольшего расстояния, тогда этих точки — это вершины прямоугольного треугольника.
Ширина (по горизонтали), высота (идущий вертикально), и провод (идущий по диагонали) для ворота образуют прямоугольный треугольник.Когда ворота квадратные, диагональ будет подчиняться теореме Пифагора. авторское право Элизабет Стапель 2010-2011 Все права защищены Таким образом, длина растяжек будет девять футов. длинный плюс еще 0,43389 футов или около того. В одном футе двенадцать дюймов, поэтому: Будет еще около 5,2 дюймы; 0,2 ближе к 0,25 чем до 0,0, итак: Длина провода будет 9 футов, 5 1 / 4 дюймов.
Обратите внимание, что для того, чтобы ответ был правильным, отображаемая картинка никак не может быть «в масштабе». Вам следует Разумеется, предполагаем, что рисунки для геометрии и тригонометрии упражнения , а не «в масштабе».Разве , а не , делает ошибка попытки угадать ответы по картинкам! << Предыдущая Вверх | 1 | 2 | Вернуться к индексу
|
Иллюстративная математика
Задача
Существует ли равносторонний треугольник $ ABC $, так что $ \ overline {AB} $ лежит на оси $ x $, а все $ A $, $ B $ и $ C $ имеют целые координаты $ x $ и $ y $? ? Объяснять.
Комментарий IM
Цель этой задачи — изучить углы треугольников, вершины которых имеют определенные целочисленные координаты. Исследуемые углы образованы тремя точками с целыми координатами, две из которых находятся на оси $ x $. Таких углов много, поскольку единственным ограничением негоризонтального луча является то, что он принадлежит прямой с рациональным наклоном. Оказывается, влияние рациональности этого наклона состоит в том, что при этих условиях угол в 60 градусов становится невозможным, и поэтому не существует равностороннего треугольника, удовлетворяющего этим ограничениям.Студенты должны будут знать или уметь рассчитать длину равностороннего треугольника или знать синус и косинус угла в 60 градусов. Это можно сделать с помощью знания тригонометрических функций или теоремы Пифагора. Учителю, возможно, потребуется дать совет: хорошей отправной точкой было бы нарисовать несколько треугольников, как в решении, и определить, являются ли эти частные случаи равносторонними.
Задачу можно естественным образом расширить, чтобы показать, что на плоскости нет равностороннего треугольника, вершины которого имеют целочисленные координаты: другими словами, ответ на задачу тот же, без предположения, что две из вершин находятся на $ x $ — ось.Аргумент этой более общей проблемы представлен с использованием формул суммы и разности для касательной функции. Это плюс стандарта, и формулы, вероятно, необходимо будет предоставить. Однако важны не сами точные формулы, а их структура: эту задачу можно рассматривать не только как применение этих формул, но и как мотивацию для их исследования.
Идея этого задания возникла на собрании кружка учителей математики в Альбукерке 1 октября 2013 года.
Решения
Решение: 1 Тригонометрические функции
Предположим, что существует равносторонний треугольник $ ABC $, удовлетворяющий заданным условиям. Мы можем сделать горизонтальный сдвиг так, чтобы $ A = (0,0) $, и для простоты будем предполагать, что $ B $ лежит на положительной оси $ x $. Ниже приведено изображение примера, в котором координата $ y $ для $ C $ положительна:
Предположим, что $ m (\ angle A) = 60 $. Мы можем вычислить тригонометрические функции для $ \ angle A $, составив прямоугольный треугольник, как показано ниже:
Поскольку линии сетки перпендикулярны, $ \ angle O $ в $ \ треугольнике AOC $ является прямым углом, и мы имеем $$ \ tan (\ angle A) = \ frac {| OC |} {| AO |}.$$ Для конкретного треугольника, который мы нарисовали, $ | OC | = 5 $ и $ | АО | = 2 $, но в общем случае, если $ C $ имеет целочисленные координаты (a, b), то мы получим рациональное число $ \ frac {b} {a} $ для значения $ \ tan (\ angle A) $. Поскольку $ \ tan (60) = \ sqrt {3} $ и $ \ sqrt {3} $ — иррациональное число, это означает, что $ m (\ angle BAC) $ не может быть 60. Дробь $ \ frac {b} {a} $, задающий значение $ \ tan {\ angle A} $, имеет смысл только тогда, когда $ a \ neq 0 $, но если $ a = 0 $, тогда $ \ angle A $ будет прямым углом, а $ \ треугольник ABC $ все равно не будет равносторонним.Следовательно, не существует равностороннего треугольника $ ABC $ с двумя вершинами на оси $ x $ и всеми вершинами, имеющими целочисленные координаты.
Решение: 2 Теорема Пифагора
Предположим, что существует равносторонний треугольник $ ABC $, удовлетворяющий заданным условиям. Мы можем сделать горизонтальный сдвиг так, чтобы $ A = (0,0) $, и для простоты будем предполагать, что $ B $ лежит на положительной оси $ x $. На рисунке $ \ overleftrightarrow {CO} $ перпендикулярен $ \ overleftrightarrow {AB} $.2 $ и, следовательно, $$ \ sqrt {3} | АО | = | OC | $$ и $ \ sqrt {3} = \ frac {| OC |} {| AO |} $. Если бы $ \ треугольник ABC $ был равносторонним, то $ | AC | = | AB | $ и $ | AO | = \ frac {| AB |} {2} $ — рациональные числа. Это означало бы, что $ \ sqrt {3} $ — рациональное число. Однако это неверно, поэтому $ \ треугольник ABC $ не может быть равносторонним.
Решение: 3 формулы сложения для тригонометрических функций (F-TF.9)
Это решение основано на первом решении с использованием тригонометрии. Цель здесь — использовать формулу суммы / разности для касательной функции, которая гласит, что $$ \ tan {(a \ pm b)} = \ frac {\ tan {a} \ pm \ tan {b}} {1 \ mp \ tan {a} \ tan {b}}.$$ Напомним, что $ \ tan {x} = \ frac {\ sin {x}} {\ cos {x}} $, и это имеет смысл когда $ \ cos {x} \ neq 0 $. Таким образом, мы должны убедиться в нашем аргументе ниже, что $ a, b, $ и $ a \ pm b $ не являются $ \ pm 90 $. Отметим также, что разные знаки касательных выражений в числителе и знаменателе.
Ниже приведен рисунок, показывающий конкретный треугольник, к которому мы можем применить приведенную выше формулу суммы:
В этом случае мы имеем $ m (\ angle A) = a + b $ и, используя формулу выше
$$ \ begin {align} \ tan {\ angle A} & = \ tan {(a + b)} \\ & = \ frac {\ tan {a} + \ tan {b}} {1 — \ tan {a} \ tan {b}}.\ end {align} $$
Как видно из первого решения, $ \ tan {a} $ и $ \ tan {b} $ являются рациональными числами: в этом случае $ \ tan {a} = \ frac {1} {3} $ и $ \ tan {b} = \ frac {2} {2} $. Используя формулу выше, мы находим, что $ \ tan {\ angle A} $ — рациональное число. С другой стороны, если $ m (\ angle A) = 60 $, то $ \ tan {A} = \ sqrt {3} $, иррациональное число. Таким образом, это невозможно для $ m (\ angle A) = 60 $, и невозможно, чтобы $ \ Triangle ABC $ был равносторонним треугольником.
Любой треугольник, вершины которого имеют целые координаты, можно перевести так что одна из вершин, скажем, $ A $, находится в точке (0,0), а две другие вершины имеют целочисленные координаты.Мы также можем применить поворот на 90 градусов относительно начала координат (который преобразует целочисленные координаты в целочисленные координаты), чтобы одна из других вершин, которые мы помечаем как $ C $, лежала в первом квадранте и $ m (\ angle BAC) \ gt 0 $. Единственный способ, которым треугольник может быть равносторонним, — это если третья вершина $ B $ лежит либо в четвертом квадранте, либо в первом квадранте. Случай, когда $ B $ лежит в четвертом квадранте, был рассмотрен выше (знаменатель $ 1 — \ tan {a} \ tan {b} $ не может быть нулевым, если $ \ angle A $ равен углу 60 градусов).Если $ B $ лежит в первом квадранте, применяется аналогичный аргумент с использованием формулы тангенса разности двух углов. Изображение этой другой ситуации дано ниже:
Площадь треугольника в координатной геометрии — Формула
В геометрии треугольник — это трехсторонний многоугольник, имеющий три ребра и три вершины. Площадь треугольника — это пространство, покрытое треугольником в двухмерной плоскости. Формула площади треугольника: (1/2) × основание × высота.Выясним площадь треугольника в координатной геометрии.
Какова площадь треугольника в координатной геометрии?
Координатная геометрия определяется как изучение геометрии с использованием координатных точек. Площадь треугольника в координатной геометрии может быть вычислена, если три вершины треугольника заданы в координатной плоскости. Площадь треугольника в координатной геометрии определяется как площадь или пространство, покрываемое им в двумерной координатной плоскости.Давайте лучше поймем понятие площади треугольника в координатной геометрии на примере, приведенном ниже,
Рассмотрим эти три точки: A (−2,1), B (3,2), C (1,5). Если вы нанесете эти три точки на плоскость, вы обнаружите, что они неколлинеарны, что означает, что они могут быть вершинами треугольника, как показано ниже:
Область, охватываемая треугольником ABC в плоскости x-y, — это область, отмеченная синим цветом. Теперь с помощью координатной геометрии мы можем найти площадь этого треугольника.Давайте узнаем об этом больше в следующем разделе.
Как вычислить площадь треугольника в координатной геометрии?
В координатной геометрии, если нам нужно найти площадь треугольника, мы используем координаты трех вершин. Рассмотрим ▵ABC, как показано на рисунке ниже, с вершинами A (x \ (_ 1 \), y \ (_ 1 \)), B (x \ (_ 2 \), y \ (_ 2 \)) и C (x \ (_3 \), у \ (_ 3 \)). На этом рисунке мы нарисовали перпендикуляры AE, CF и BD от вершин треугольника к горизонтальной оси.Обратите внимание, что сформированы три трапеции: BAED, ACFE и BCFD.
Мы можем выразить площадь треугольника через площади этих трех трапеций.
Площадь (ΔABC) = Площадь (Trap.BAED) + Площадь (Trap.ACFE) — Площадь (Trap.BCFD)
Теперь площадь трапеции, выраженная в длинах параллельных сторон (оснований трапеции) и расстоянии между параллельными сторонами (высота трапеции):
Площадь трапеции = (1/2) × Сумма оснований × Высота
Рассмотрим любую трапецию, скажем BAED.Его основания — BD и AE, а высота — DE. BD и AE можно легко увидеть как координаты x точек B и A, а DE — это разность между координатами x точек A и B. Аналогичным образом можно легко вычислить основания и высоту двух других трапеций. . Таким образом, имеем:
Площадь (Trap.BAED) = (1/2) × (BD + AE) × DE
= (1/2) × (y \ (_ 2 \) + y \ (_ 1 \)) × (x \ (_ 1 \) — x \ (_ 2 \))
Площадь (Trap.ACFE) = (1/2) × (AE + CF) × EF
= (1/2) × (y \ (_ 1 \) + y \ (_ 3 \)) × (x \ (_ 3 \) — x \ (_ 1 \))
Площадь (Ловушка.BCFD) = (1/2) × (BD + CF) × DF
= (1/2) × (y \ (_ 2 \) + y \ (_ 3 \)) × (x \ (_ 3 \) — x \ (_ 2 \))
Таким образом, выражение для площади треугольника через координаты его вершин может быть записано как,
Площадь (ΔABC) = Площадь (Trap.BAED) + Площадь (Trap.ACFE) — Площадь (Trap.BCFD)
= (1/2) × [(y \ (_ 2 \) + y \ (_ 1 \)) × (x \ (_ 1 \) — x \ (_ 2 \))] + (1/2) × [( y \ (_ 1 \) + y \ (_ 3 \)) × (x \ (_ 3 \) — x \ (_ 1 \))] — (1/2) × [(y \ (_ 2 \) + y \ ( _3 \)) × (х \ (_ 3 \) — х \ (_ 2 \))]
Однако мы должны попытаться упростить его, чтобы его было легко запомнить.
Для этого упростим произведение двух скобок в каждом термине:
= (1/2) (x \ (_ 1 \) y \ (_ 2 \) — x \ (_ 2 \) y \ (_ 2 \) + x \ (_ 1 \) y \ (_ 1 \) — x \ ( _2 \) y \ (_ 1 \)) + (1/2) (x \ (_ 3 \) y \ (_ 1 \) — x \ (_ 1 \) y \ (_ 1 \) + x \ (_ 3 \) y \ (_ 3 \) — x \ (_ 1 \) y \ (_ 3 \)) — (1/2) (x \ (_ 3 \) y \ (_ 2 \) — x \ (_ 2 \) y \ (_ 2 \ ) + х \ (_ 3 \) у \ (_ 3 \) — х \ (_ 2 \) у \ (_ 3 \))
Возьмите общий член 1/2 за скобки.
= (1/2) (x \ (_ 1 \) y \ (_ 2 \) — x \ (_ 2 \) y \ (_ 2 \) + x \ (_ 1 \) y \ (_ 1 \) — x \ ( _2 \) y \ (_ 1 \) — x \ (_ 3 \) y \ (_ 1 \) — x \ (_ 1 \) y \ (_ 1 \) + x \ (_ 3 \) y \ (_ 3 \) — x \ (_ 1 \) y \ (_ 3 \) — x \ (_ 3 \) y \ (_ 2 \) + x \ (_ 2 \) y \ (_ 2 \) — x \ (_ 3 \) y \ (_ 3 \) + х \ (_ 2 \) у \ (_ 3 \))
Таким образом,
Площадь (ΔABC) = (1/2) {x \ (_ 1 \) (y \ (_ 2 \) — y \ (_ 3 \)) + x \ (_ 2 \) (y \ (_ 3 \) — y \ (_1 \)) + х \ (_ 3 \) (у \ (_ 1 \) — у \ (_ 2 \))}
Так как район всегда положительный.
(ΔABC) = (1/2) | x \ (_ 1 \) (y \ (_ 2 \) — y \ (_ 3 \)) + x \ (_ 2 \) (y \ (_ 3 \) — y \ ( _1 \)) + х \ (_ 3 \) (у \ (_ 1 \) — у \ (_ 2 \)) |
Это симметричное выражение, и его легко запомнить, который мы сейчас обсудим как метод детерминант.
Площадь треугольника с использованием метода определения
Чтобы вычислить площадь треугольника с помощью определителей, мы используем формулу, показанную ниже:
Площадь = 1/2 \ (\ begin {bmatrix} {{x_1}} & {{y_1}} & {{1}} \\ {{x_2}} & {{y_2}} & {{1}} \ \ {x_3} & {y_3} & 1 \ end {bmatrix} \)
Давайте решим приведенное выше выражение, чтобы получить формулу для площади треугольника с использованием координат.Решим определитель по первому столбцу.
Теперь первый член в выражении для площади равен \ ({x_1} \ left ({{y_2} — {y_3}} \ right) \). Чтобы получить это, мы решаем определитель для первого члена в первом столбце. Игнорируйте термины в первой строке и столбце, отличные от первого члена, и действуйте в соответствии со следующим визуальным представлением ( крестообразные стрелки представляют умножение ). Решая определитель, мы получаем x \ (_ 1 \) (y \ (_ 2 \) — y \ (_ 3 \)).
Второй член в выражении для площади — это x \ (_ 2 \) (y \ (_ 3 \) — y \ (_ 1 \)).Чтобы получить это, мы решаем определитель для второго члена в первом столбце. Игнорируйте термины во второй строке и первом столбце, кроме первого члена во втором столбце. Решая определитель, получаем -x \ (_ 2 \) (y \ (_ 1 \) — y \ (_ 3 \)) = x \ (_ 2 \) (\ ({y_3} — {y_1} \)):
Затем третий член в выражении для площади равен \ ({x_3} \ left ({{y_1} — {y_2}} \ right) \). Чтобы получить это, мы решаем определитель для третьего члена в первом столбце. Игнорируйте термины в первой строке и третьем столбце, кроме первого члена в третьем столбце:
Наконец, мы складываем эти три члена, чтобы получить площадь (и делим его на коэффициент 2, потому что у нас был этот коэффициент в исходном выражении, которое мы определили):
Площадь = (1/2) | x \ (_ 1 \) (y \ (_ 2 \) — y \ (_ 3 \)) + x \ (_ 2 \) (y \ (_ 3 \) — y \ (_ 1 \ )) + х \ (_ 3 \) (у \ (_ 1 \) — у \ (_ 2 \)) |
Обратите внимание, что мы поместили знак модуля (вертикальные полосы) вокруг нашего алгебраического выражения и удалили отрицательный знак, потому что площадь всегда положительна, что мы получили в исходном выражении.Таким образом, даже если мы получим отрицательное значение через алгебраическое выражение, знак модуля гарантирует, что оно будет преобразовано в положительное значение.
Вышеупомянутое выражение для площади можно записать компактно следующим образом:
\ (A = \ frac {1} {2} \; \ left | {\ begin {array} {* {20} {c}} {{x_1}} & {{y_1}} & {{1}} \\ {{x_2}} & {{y_2}} & {{1}} \\ {x_3} & {y_3} & 1 \ end {array}} \ right | \)
Важные примечания:
- Площадь треугольника не может быть отрицательной.В случае, если мы получили отрицательный ответ, следует учитывать числовое значение площади без знака «минус».
- Чтобы найти площадь треугольника в координатной геометрии, нам нужно найти длину трех сторон треугольника, используя формулу расстояния.
Если три точки A (x \ (_ 1 \), y \ (_ 1 \)), B (x \ (_ 2 \), y \ (_ 2 \)) и C (x \ (_ 3 \), y \ (_3 \)) коллинеарны, тогда x \ (_ 1 \) (y \ (_ 2 \) — y \ (_ 3 \)) + x \ (_ 2 \) (y \ (_ 3 \) — y \ (_ 1 \ )) + х \ (_ 3 \) (у \ (_ 1 \) — у \ (_ 2 \)) = 0.
Сложные вопросы
Решенные примеры площади треугольника в координатной геометрии
Пример 1: Рассмотрим треугольник со следующими вершинами: A (−1,2), B (2,3), C (4, −3). Найти площадь этого треугольника в координатной геометрии?
Решение: Для иллюстрации мы вычислим каждый из трех членов формулы для площади отдельно, а затем сложим их вместе, чтобы получить окончательное значение.
\ (\ left | {\ begin {array} {* {20} {c}} {- 1} & 2 & 4 \\ 2 & 3 & {- 3} \\ 1 & 1 & 1 \ end {array}} \ right | \)
Воспользуемся формулой определителя, чтобы найти площадь данного треугольника.
Площадь ΔABC = 1/2 \ (\ left | {\ begin {array} {* {20} {c}} {- 1} & 2 & 4 \\ 2 & 3 & {- 3} \\ 1 & 1 & 1 \ end {array}} \ справа | \)
Площадь ΔABC = 1/2 | -1 (3 — (-3)) — 2 (2 — (-3)) + 4 (2-3) |
Площадь (ΔABC) = (1/2) | (−6) — (10) + (−4) | = (1/2) × 20 = 10 кв.ед.
∴ Площадь треугольника составляет 10 единиц квадрата.
Пример 2: Найдите площадь треугольника с вершинами: A (3,4), B (4,7) и C (6, −3).
Раствор:
У нас:
(ΔABC) = (1/2) | x \ (_ 1 \) (y \ (_ 2 \) — y \ (_ 3 \)) + x \ (_ 2 \) (y \ (_ 3 \) — y \ ( _1 \)) + х \ (_ 3 \) (y \ (_ 1 \) — y \ (_ 2 \)) |
(ΔABC) = (1/2) | 3 (7 — (−3)) + 4 ((- 3) — (−4)) + 6 (4 — (7)) | = 12 | 30 + 4 — 18 | = (1/2) × 16 = 8кв.ед.
Пример 3: Найдите площадь треугольника в координатной геометрии, вершины которого: A (1, −2), B (−3,4), C (2,3)
Раствор:
Площадь ΔABC = 1/2 \ (\ left | {\ begin {array} {* {20} {c}} 1 & {- 2} & 1 \\ {- 3} & 4 & 1 \\ 2 & 3 & 1 \ end {array}} \ справа | \)
Площадь ΔABC = (1/2) | x \ (_ 1 \) (y \ (_ 2 \) — y \ (_ 3 \)) + x \ (_ 2 \) (y \ (_ 3 \) — y \ ( _1 \)) + х \ (_ 3 \) (у \ (_ 1 \) — у \ (_ 2 \)) |
(1/2) | 1 × (4–3) — 3 × ((3) + 2)) + 2 (−2–4) | = (1/2) | 1 -15 — 12 | = 13 кв.ед.
∴Площадь треугольника 13 кв. Шт.
перейти к слайду перейти к слайду
Разбивайте сложные концепции с помощью простых визуальных элементов.
Математика больше не будет сложным предметом, особенно если вы понимаете концепции посредством визуализации.
Забронируйте бесплатную пробную версию Class
Часто задаваемые вопросы о площади треугольника в координатной геометрии
Как определить длину стороны треугольника по координатам?
Формула расстояния используется для определения длины треугольника по координатам.Формулу расстояния можно использовать, чтобы найти длину любой стороны по координатам вершин треугольника.
Какова формула площади треугольника в координатной геометрии?
Формула площади треугольника в координатной геометрии площадь треугольника в координатной геометрии равна: A = (1/2) | x \ (_ 1 \) (y \ (_ 2 \) — y \ (_ 3 \)) + х \ (_ 2 \) (у \ (_ 3 \) — у \ (_ 1 \)) + х \ (_ 3 \) (у \ (_ 1 \) — у \ (_ 2 \)) |, где (х \ ( _1 \), y \ (_ 1 \)), (x \ (_ 2 \), y \ (_ 2 \)) и (x \ (_ 3 \), y \ (_ 3 \)) — координаты вершин треугольник.
Как определить площадь и периметр треугольника с координатами?
Для площади и периметра треугольника с координатами сначала мы должны найти расстояние между каждой парой точек по формуле расстояния, а затем применить формулу для площади и периметра.
Как найти площадь треугольника с тремя координатами?
Площадь треугольника с 3 точками: A = (1/2) | x \ (_ 1 \) (y \ (_ 2 \) — y \ (_ 3 \)) + x \ (_ 2 \) (y \ (_ 3 \) — y \ (_ 1 \)) + x \ (_ 3 \) (y \ (_ 1 \) — y \ (_ 2 \)) |, где (x \ (_ 1 \), y \ (_ 1 \)) , (x \ (_ 2 \), y \ (_ 2 \)) и (x \ (_ 3 \), y \ (_ 3 \)) — координаты вершин треугольника.
Как найти площадь треугольника по вершинам?
Формула площади треугольника в координатной геометрии: A = (1/2) | x \ (_ 1 \) (y \ (_ 2 \) — y \ (_ 3 \)) + x \ (_ 2 \) ( y \ (_ 3 \) — y \ (_ 1 \)) + x \ (_ 3 \) (y \ (_ 1 \) — y \ (_ 2 \)) |, где (x \ (_ 1 \), y \ ( _1 \)), (x \ (_ 2 \), y \ (_ 2 \)) и (x \ (_ 3 \), y \ (_ 3 \)) являются вершинами треугольника.
Как определить площадь равнобедренного треугольника по координатам?
Во-первых, мы используем формулу расстояния, чтобы вычислить длину каждой стороны треугольника.Если две стороны равны, это равнобедренный треугольник. Мы можем применить формулу площади равнобедренного треугольника, используя длины сторон.
Как определить площадь прямоугольного треугольника по координатам?
Во-первых, мы используем формулу расстояния, чтобы вычислить длину каждой стороны треугольника. Если квадраты двух меньших расстояний равны квадрату наибольшего расстояния, то эти точки являются вершинами прямоугольного треугольника. или мы можем использовать теорему Пифагора.Мы можем применить формулу площади прямоугольного треугольника, используя длины сторон.
Как вычислить площадь треугольника на графике?
Площадь треугольника на графике рассчитывается по формуле площади: A = (1/2) | x \ (_ 1 \) (y \ (_ 2 \) — y \ (_ 3 \)) + x \ (_ 2 \) (y \ (_ 3 \) — y \ (_ 1 \)) + x \ (_ 3 \) (y \ (_ 1 \) — y \ (_ 2 \)) |, где (x \ (_ 1 \), y \ (_ 1 \)), (x \ (_ 2 \), y \ (_ 2 \)) и (x \ (_ 3 \), y \ (_ 3 \)) являются вершинами треугольника.
Как найти недостающую координату прямоугольного треугольника?
Мы используем формулу расстояния и теорему Пифагора для вычисления недостающей координаты прямоугольного треугольника.
Калькулятор ортоцентра|| Определение || Формула
Добро пожаловать в калькулятор ортоцентра — инструмент, с помощью которого вы легко можете найти ортоцентр любого треугольника , будь то прямой, тупой или острый. Если вы не уверены, что такое ортоцентр треугольника, мы подготовили хорошее объяснение, а также определение ортоцентра. После этого вы можете научиться найти ортоцентр с помощью пошагового набора инструкций (или вы можете просто использовать формулу ортоцентра , основанную на тригонометрии).И, когда вы проработали все это, вас ждут некоторые свойства ортоцентра и некоторые бонусные особые случаи …
Что такое ортоцентр треугольника? Определение ортоцентра
Ортоцентр треугольника — это точка, где высоты треугольника пересекаются с . Три высоты треугольника всегда совпадают, что означает, что они встречаются в одной точке. Напоминаем, что высота — это отрезок линии, перпендикулярный стороне и касающийся угла, противоположного стороне.
Как найти ортоцентр?
Теперь, когда вы познакомились с определением ортоцентра, давайте посмотрим, как его найти. Самый простой и понятный способ вычислить ортоцентр треугольника — следовать этому пошаговому руководству:
Для начала предположим, что треугольник ABC имеет координаты вершины A = (x₁, y₁), B = (x₂, y₂) и C = (x₃, y₃).
- Найдите наклон одной стороны треугольника, например AB. Используйте формулу наклона:
наклон = (y₂ - y₁) / (x₂ - x₁)
- Рассчитайте уклон, перпендикулярный стороне AB.Таким образом, вы найдете наклон высоты треугольника для этой стороны. Уравнение для наклона высоты:
перпендикулярный уклон = - 1 / уклон
- Затем вам нужно найти уравнение для прямой, содержащей высоту треугольника — той, которая проходит через вершину C (x₃, y₃). Используйте уравнение для формулы наклона точки:
y - Y = m * (x - X)
Для нашего примера это будет:
y - y₃ = m * (x - x₃) , где m = –1 / slope = - (x₂ - x₁) / (y₂ - y₁)
следовательно,
y = y₃ - (x₂ - x₁) * (x - x₃) / (y₂ - y₁)
- Повторите шаги для другой стороны, AC или BC.
y = y₂ - (x₃ - x₁) * (x - x₂) / (y₃ - y₁)
- Решите систему линейных уравнений (два уравнения в форме пересечения наклона), чтобы найти ортоцентр.
Как найти ортоцентр — пример
Уравнения в приведенном выше абзаце могут выглядеть пугающе, но вам не о чем беспокоиться, это не так уж и сложно! Давайте проверим, как найти ортоцентр на примере, где наш треугольник ABC имеет координаты вершины: A = (1, 1), B = (3, 5), C = (7, 2).
- Найдите уклон:
Боковой уклон АВ = (5-1) / (3-1) = 2
- Рассчитать наклон перпендикулярной прямой:
Наклон перпендикуляра к стороне AB = - 1/2
- Найдите уравнение прямой:
y - 2 = - 1/2 * (x - 7) поэтому y = 5.5 - 0.5 * x
- Повторить для другой стороны, например, BC;
Боковой откос BC = (2-5) / (7-3) = - 3/4
уклон перпендикулярно к стороне ВС = 4/3
y - 1 = 4/3 * (x - 1) , поэтому y = -1/3 + 4/3 * x
- Решите систему линейных уравнений:
y = 5.5 - 0,5 * x и
y = -1/3 + 4/3 * x
т.
5,5 - 0,5 * х = -1/3 + 4/3 * х
35/6 = х * 11/6
x = 35/11 ≈ 3,182 .
Подставив x в любое уравнение, мы получим:
y = 43/11 ≈ 3,909
Конечно, такой же результат вы получите и с нашим калькулятором ортоцентра💪! Просто введите три вершины треугольника, и мы рассчитаем для вас координаты ортоцентра.
Формула ортоцентра
Существует более компактная формула для поиска ортоцентра треугольника, но вы должны быть знакомы с концепцией касательной. Чтобы найти координаты ортоцентра H = (x, y), вам необходимо решить следующие уравнения:
x = (x1 * tan (α) + x2 * tan (β) + x3 * tan (γ)) / (tan (α) + tan (β) + tan (γ))
y = (y1 * tan (α) + y2 * tan (β) + y3 * tan (γ)) / (tan (α) + tan (β) + tan (γ))
Хотя эти формулы ортоцентра могут выглядеть намного проще, чем предыдущие инструкции о том, как найти координаты центра, у вас, вероятно, нет углов треугольника, α, β и γ, при условии, не так ли?
Так что вам, вероятно, нужно сначала их найти.Используйте теорему Пифагора, чтобы найти длину сторон треугольника. Затем примените закон косинусов, чтобы найти углы треугольника. Все это встроено в наш калькулятор ортоцентра.
Свойства ортоцентра и мелочи
Есть несколько интересных свойств ортоцентра! Ортоцентр:
- совпадает с центром описанной окружности, центром и центром тяжести равностороннего треугольника,
- совпадает с прямоугольной вершиной для прямоугольных треугольников,
- лежит внутри треугольника для острых треугольников ,
- лежит вне треугольника в тупых треугольниках.
Знаете ли вы, что …
- три вершины треугольника и ортоцентр треугольника этих точек образуют ортоцентрическую систему . Если вы сделаете треугольник из любых трех точек, оставшаяся одна будет его ортоцентром.
- Отражение ортоцентра над любой из трех сторон лежит на описанной окружности треугольника.
- угол, образованный в ортоцентре, является дополнительным к углу при вершине.
- в каждом неравностороннем треугольнике есть линия , проходящая через все важные центры треугольника (ортоцентр, центроид, центр описанной окружности, окружность из девяти точек) — это линия Эйлера .
Конгруэнтные треугольники на координатной плоскости
Два треугольника называются конгруэнтный если есть изометрия сопоставление одного из треугольников с другим. (Изометрия — это трансформация , Такие как перевод , вращение , или отражение , который не меняет расстояние между любыми двумя точками.)
Представьте, что два треугольника вырезаны из бумаги. Если вы можете положить один на другой и точно сопоставить его форму, тогда два треугольника будут конгруэнтны.На приведенном выше рисунке Δ А B C соответствует Δ D E F .
Напомним теорему сравнения SSS: если три стороны одного треугольника конгруэнтны трем сторонам второго треугольника, то два треугольника конгруэнтны.Имея два треугольника на координатной плоскости, вы можете проверить, совпадают ли они, используя формула расстояния чтобы найти длину их сторон. Если три пары сторон конгруэнтны, то треугольники конгруэнтны по указанной выше теореме.
Если А B ¯ ≅ п Q ¯ , B C ¯ ≅ Q р ¯ , а также А C ¯ ≅ п р ¯ , тогда Δ А B C ≅ Δ п Q р .
Пример:
.
Убедитесь, что эти треугольники конгруэнтны, используя формулу расстояния и теорему сравнения SSS.
Решение:
Найдите длины сторон, используя формулу расстояния.
Расстояние знак равно ( Икс 2 — Икс 1 ) 2 + ( у 2 — у 1 ) 2
Треугольник А B C имеет вершины А ( — 3 , — 1 ) , B ( — 5 , — 4 ) а также C ( — 2 , — 5 ) .
А B ¯ знак равно ( — 5 — ( — 3 ) ) 2 + ( — 4 — ( — 1 ) ) 2 знак равно 13 B C ¯ знак равно ( — 2 — ( — 5 ) ) 2 + ( — 5 — ( — 4 ) ) 2 знак равно 10 А C ¯ знак равно ( — 2 — ( — 3 ) ) 2 + ( — 5 — ( — 1 ) ) 2 знак равно 17
Треугольник п Q р имеет вершины п ( 4 , 5 ) , Q ( 2 , 2 ) а также р ( 5 , 1 ) .
Следовательно,
п Q ¯ знак равно ( 2 — 4 ) 2 + ( 2 — 5 ) 2 знак равно 13 Q р ¯ знак равно ( 5 — 2 ) 2 + ( 1 — 2 ) 2 знак равно 10 п р ¯ знак равно ( 5 — 4 ) 2 + ( 1 — 5 ) 2 знак равно 17
Здесь соответствующие стороны двух треугольников имеют одинаковую длину:
А B ¯ ≅ п Q ¯ , B C ¯ ≅ Q р ¯ , а также А C ¯ ≅ п р ¯
Итак, по теореме сравнения SSS, Δ А B C ≅ Δ п Q р .
Как определить по координатам скален, равнобедренный и равносторонний треугольники | Геометрия
Как определить скален, равнобедренный и равносторонний треугольники по координатам
Шаг 1: Обозначьте данные точки как A, B и C и начертите их как вершины треугольника с соединительными линиями, чтобы нарисовать треугольник, над которым мы работаем.
Шаг 2: Рассчитайте длину стороны AB по формуле расстояния.
Шаг 3: Рассчитайте длину стороны BC по формуле расстояния.
Шаг 4: Рассчитайте длину стороны AC по формуле расстояния.
Шаг 5: Сравните длины сторон AB, BC и AC из предыдущих шагов, чтобы определить тип треугольника.
Как определить скален, равнобедренные и равносторонние треугольники по словарю координат и формуле
Масштабный треугольник: Разносторонний треугольник — это треугольник, все три стороны которого имеют разную длину, а все три угла имеют разные значения.{\ circ} {/ экв}.
Формула расстояния: Формула расстояния, полученная из теоремы Пифагора, может использоваться для определения расстояния между двумя точками, {eq} (x_ {1}, y_ {1}) {/ eq} и {eq} (x_ {2}, y_ {2}) {/ экв}.{2})} {/ eq}
Теперь мы рассмотрим три пошаговых примера, где даны три координатные точки, и мы хотим классифицировать тип треугольника, который они представляют. Первый пример будет для разностороннего треугольника, второй пример будет для равнобедренного треугольника, а третий пример будет для равностороннего треугольника.
Как определить скален, равнобедренный и равносторонний треугольники по координатам Пример: Скален
Треугольник имеет следующие вершины: A (0, 0), B (2, 2) и C (3, -4).Тип треугольника {eq} \ bigtriangleup ABC {/ eq}?
Шаг 1: Обозначьте данные точки как A, B и C и начертите их как вершины треугольника с соединительными линиями, чтобы нарисовать треугольник, над которым мы работаем.
У нас есть следующие точки координат:
А: (0, 0)
Б: (2, 2)
К: (3, -4)
На графике мы имеем следующий треугольник {eq} \ bigtriangleup ABC {/ eq}:
Шаг 2: Вычислите длину стороны AB по формуле расстояния.{2}} = \ sqrt {9 + 16} = \ sqrt {25} = 5 {/ eq}
Сторона AC имеет длину 5.
Шаг 5: Сравните длины сторон AB, BC и AC из предыдущих шагов, чтобы определить тип треугольника.
Длины сторон нашего треугольника равны {eq} \ sqrt {8} {/ eq}, {eq} \ sqrt {37} {/ eq} и 5.
Поскольку все стороны имеют разную длину, мы знаем, что это разносторонний треугольник.
{eq} \ mathbf {\ bigtriangleup ABC} {/ eq} с вершинами A (0, 0), B (2, 2) и C (3, -4) представляет собой разносторонний треугольник.
Как определить скален, равнобедренный и равносторонний треугольники по координатам Пример: равнобедренный треугольник
Треугольник имеет следующие вершины: A (-6, -2), B (-2, 3) и C (2, -2). Тип треугольника {eq} \ bigtriangleup ABC {/ eq}?
Шаг 1: Обозначьте данные точки как A, B и C и начертите их как вершины треугольника с соединительными линиями, чтобы нарисовать треугольник, над которым мы работаем.
У нас есть следующие моменты.{2}} = \ sqrt {64} = 8 {/ eq}
Сторона переменного тока имеет длину 8.
Шаг 5: Сравните длины сторон AB, BC и AC из предыдущих шагов, чтобы определить тип треугольника.
Стороны треугольника равны {eq} \ sqrt {41}, \ sqrt {41}. {/ eq} и 8.
Поскольку две стороны имеют одинаковую длину, это равнобедренный треугольник.
{eq} \ mathbf {\ bigtriangleup ABC} {/ eq} с вершинами A (-6, -2), B (-2, 3) и C (2, -2) — равнобедренный треугольник.
Как определить скален, равнобедренный и равносторонний треугольники по координатам Пример: равносторонний
Треугольник имеет следующие вершины: A (-1, 1.5), B (1, -2) и C (3, 1.5). Тип треугольника {eq} \ bigtriangleup ABC {/ eq}?
Шаг 1: Обозначьте данные точки как A, B и C и начертите их как вершины треугольника с соединительными линиями, чтобы нарисовать треугольник, над которым мы работаем.
А: (-1, 1.{2}} = \ sqrt {16} = 4 {/ eq}
Сторона переменного тока имеет длину 4.
Шаг 5: Сравните длины сторон AB, BC и AC из предыдущих шагов, чтобы определить тип треугольника.
Все стороны имеют длину 4, так что это равносторонний треугольник.
{eq} \ mathbf {\ bigtriangleup ABC} {/ eq} с вершинами A (-1, 1.5), B (1, -2) и C (3, 1.5) представляет собой равносторонний треугольник.
Получите доступ к тысячам практических вопросов и объяснений!Докажите равнобедренный треугольник с помощью координатной геометрии
Равнобедренный треугольник имеет 2 совпадающие стороны и два конгруэнтных угла.Самый простой способ доказать, что треугольник равнобедренный с использованием Координатная геометрия заключается в использовании сторон.