Замещение и совмещение \ Акты, образцы, формы, договоры \ Консультант Плюс

]]>

Подборка наиболее важных документов по запросу Замещение и совмещение (нормативно–правовые акты, формы, статьи, консультации экспертов и многое другое).

Судебная практика: Замещение и совмещение Открыть документ в вашей системе КонсультантПлюс:
Подборка судебных решений за 2019 год: Статья 12.1 «Ограничения и обязанности, налагаемые на лиц, замещающих государственные должности Российской Федерации, государственные должности субъектов Российской Федерации, муниципальные должности» Федерального закона «О противодействии коррупции»
(Р.Б. Касенов)Как указали суды, ограничение, установленное ч. 2 ст. 12.1 Федерального закона от 25.12.2008 N 273-ФЗ «О противодействии коррупции», депутатом (ответчиком) не нарушено, а запрет на одновременное замещение нескольких государственных должностей РФ касается совмещения должностей, на которых эти лица осуществляют свои полномочия на постоянной основе. Действующее законодательство о статусе военнослужащих и о порядке прохождения военной службы не содержит запрета на одновременное замещение военнослужащим воинской должности и исполнение полномочий депутата муниципального образования на непостоянной основе, не предусматривающих замещение оплачиваемой муниципальной должности. Кроме того, судом установлено, что ответчик начал исполнять обязанности депутата совета депутатов на постоянной основе на основании решения совета депутатов только после увольнения с военной службы, и поэтому требования ч. 2 ст. 12.1 Закона N 273-ФЗ депутатом не нарушены. Вместе с тем установлено, что депутатом поданы заведомо недостоверные сведения о доходах, расходах, об имуществе и обязательствах имущественного характера, в установленном законом порядке уточненная справка в целях устранения недостатков, ошибок в этих сведениях им не представлена. Таким образом, суд принял решение о досрочном прекращении по требованию губернатора полномочий депутата, в связи с несоблюдением им требований ч.

4 ст. 12.1 Закона N 273-ФЗ.

Статьи, комментарии, ответы на вопросы: Замещение и совмещение

Нормативные акты: Замещение и совмещение

Результаты конкурсов на замещение вакантных должностей государственной службы — Государственная служба — Главная — Официальный сайт Администрации Южного управленческого округа

Информация о проведенных конкурсах

 Результаты конкурса 24 августа 2020 года

24 августа 2020 года

 проведён конкурс на замещение вакантной должности и включение в кадровый резерв для замещения вакантной должности государственной гражданской службы Свердловской области —  ответственного секретаря территориальной комиссии Каменского района по делам несовершеннолетних и защите их прав.

Комиссией по проведению конкурса на замещение вакантных должностей государственной гражданской службы Свердловской области в территориальной комиссии гКаменского района по делам несовершеннолетних и защите их прав принято решение:

1) признать победителем конкурса на замещение вакантной должности государственной гражданской службы Свердловской области 

старшей группы должностей категории «специалисты» — ответственного секретаря  территориальной комиссии Каменского района по делам несовершеннолетних и защите их прав – Оксентович Юлию Викторовну;

2) признать победителем конкурса на включение в кадровый резерв для замещения вакантной должности государственной гражданской службы Свердловской области старшей группы должностей категории «специалисты» — ответственного секретаря территориальной комиссии Каменского района по делам несовершеннолетних и защите их прав – Дакалову Татьяну Геннадьевну.

 

Результаты конкурса 29 апреля 2019 года

29 апреля 2019 года состоялся конкурс  

 1) на замещение вакантных должностей государственной гражданской службы Свердловской области старшей группы должностей категории «специалисты»:

 — ведущий специалист отдела экономического и социального развития территорий Администрации Южного управленческого округа Свердловской области;

— главный специалист отдела экономического и социального развития территорий Администрации Южного управленческого округа Свердловской области; 

2)         для формирования кадрового резерва на замещение вакантных должностей государственной гражданской службы Свердловской области старшей группы должностей категории «специалисты»:

— ведущий специалист отдела экономического и социального развития территорий Администрации Южного управленческого округа Свердловской области;

— главный специалист отдела экономического и социального развития территорий Администрации Южного управленческого округа Свердловской области;

для формирования кадрового резерва на замещение вакантной должности государственной гражданской службы Свердловской области ведущей группы должностей категории «руководители»:

— начальник отдела экономического и социального развития территорий Администрации Южного управленческого округа Свердловской области.

 

Комиссией Администрации Южного управленческого округа Свердловской области по проведению конкурсов на замещение вакантных должностей государственной гражданской службы Свердловской области принято решение:

1. Признать победителем конкурса на замещение вакантной должности государственной гражданской службы Свердловской области – главный специалист отдела экономического и социального развития территорий Администрации Южного управленческого округа Свердловской области — Тимофееву Марину Николаевну.

2. Признать победителем конкурса на замещение вакантной должности государственной гражданской службы Свердловской области – ведущий специалист отдела экономического и социального развития территорий Администрации Южного управленческого округа Свердловской области — Грибанова Михаила Сергеевича;

3. Признать победителями конкурса на включение в кадровый резерв для замещения вакантной должности государственной гражданской службы Свердловской области — главный специалист отдела экономического и социального развития территорий Администрации Южного управленческого округа Свердловской области — Грибанова Михаила Сергеевича, Рябову Анну Михайловну;

4. Признать победителями конкурса на включение в кадровый резерв для замещения вакантной должности государственной гражданской службы Свердловской области — ведущий специалист отдела экономического и социального развития территорий Администрации Южного управленческого округа Свердловской области – Товкач Ирину Сергеевну, Сычеву Марину Александровну, Фетисову Валентину Александровну;

5. Признать отсутствие победителя конкурса на включение в кадровый резерв для замещения вакантной должности государственной гражданской службы Свердловской области — начальник отдела экономического и социального развития территорий Администрации Южного управленческого округа Свердловской области.

 

 

02 декабря 2016 года проведён конкурс  на замещение вакантной должности начальника отдела бюджетного учета и отчетности Администрации Южного управленческого округа Свердловской области и на включение в кадровый резерв для замещения вакантной должности государственной гражданской службы Свердловской области — начальник отдела бюджетного учета и отчетности Администрации Южного управленческого округа Свердловской области.

Комиссией по проведению конкурсов на замещение вакантных должностей государственной гражданской службы Свердловской области в Администрации Южного управленческого округа Свердловской области принято решение:

1. Признать победителем конкурса на замещение вакантной должности государственной гражданской службы Свердловской области — начальник отдела бюджетного учета и отчетности Администрации Южного управленческого округа Свердловской области Толмачеву Марину Валентиновну.

2. Признать победителем конкурса на включение в кадровый резерв для замещения вакантной должности государственной гражданской службы Свердловской области — начальник отдела бюджетного учета и отчетности Администрации Южного управленческого округа Свердловской области  Дмитриеву Розу Яковлевну.

 

 

20 октября 2016 года проведён конкурс  на замещение вакантной должности и на включение в кадровый резерв для замещения вакантной должности государственной гражданской службы Свердловской области в Администрации Южного управленческого округа Свердловской области.

Комиссией по проведению конкурсов на замещение вакантных должностей государственной гражданской службы Свердловской области в Администрации Южного управленческого округа Свердловской области принято решение:

1. Об отсутствии победителя в конкурсе на замещение вакантной должности начальника отдела бюджетного учета и отчетности и организации повторного конкурса на замещение данной должности.

2. Признать победителями конкурса на включение в кадровый резерв для замещения вакантной должности государственной гражданской службы Свердловской области — главный специалист отдела экономического и социального развития территорий Администрации Южного управленческого округа Свердловской области Глушенкова Евгения Александровича и Ершову Елену Вадутовну.

3. Признать победителем конкурса на включение в кадровый резерв для замещения вакантной должности государственной гражданской службы Свердловской области – начальник отдела экономического и социального развития территорий Администрации Южного управленческого округа Свердловской области Ялунину Татьяну Ивановну.

 

 

22 января 2016 года состоялся конкурс на включение в кадровый резерв для замещения вакантной должности государственной гражданской службы Свердловской области группы «старшие должности государственной гражданской службы Свердловской области» категории «специалисты»- ответственный секретарь территориальной комиссии Сухоложского района по делам несовершеннолетних и защите их прав.

Комиссией по проведению конкурса на включение в кадровый резерв для замещения вакантной должностигосударственной гражданской службы Свердловской области в территориальной комиссии Сухоложского района по делам несовершеннолетних и защите их прав принято решение:

— признать победителем конкурса на включение в кадровый резерв для замещения вакантной должности государственной гражданской службы Свердловской области группы «старшие должности государственной гражданской службы Свердловской области» категории «специалисты» — ответственный секретарь территориальной комиссии Сухоложского района по делам несовершеннолетних и защите их прав – Сапрыкину Аллу Николаевну.

---

24 марта 2015 года проведён конкурс на замещение вакантной должности и включение в кадровый резерв для замещения вакантной должности государственной гражданской службы Свердловской области —  ответственного секретаря территориальной комиссии города Заречного  по делам несовершеннолетних и защите их прав.

Комиссией по проведению конкурса на замещение вакантных должностей государственной гражданской службы Свердловской области в территориальной комиссии города Заречного  по делам несовершеннолетних и защите их прав принято решение:

1) признать победителем конкурса на замещение вакантной должности государственной гражданской службы Свердловской области старшей группы должностей категории «специалисты» — ответственного секретаря  территориальной комиссии города Заречного  по делам несовершеннолетних и защите их прав – Бурдукову Екатерину Викторовну;

2) признать победителем конкурса на включение в кадровый резерв для замещения вакантной должности государственной гражданской службы Свердловской области старшей группы должностей категории «специалисты» — ответственного секретаря территориальной комиссии города Заречного  по делам несовершеннолетних и защите их прав – Бойчук Анну Евгеньевну.

---

17 декабря 2014 года состоялся конкурс на включение в кадровый резерв для замещения должности государственной гражданской службы старшей группы должностей государственной гражданской службы Свердловской области – ответственный секретарь территориальной комиссии     Красногорского  района города Каменска-Уральского по делам несовершеннолетних и защите их прав.

По результатам подведения итогов конкурса победителем была признана Данилова Ольга Владимировна.

---

Конкурс на включение в кадровый резерв для замещения должности государственной гражданской службы старшей группы должностей государственной гражданской службы Свердловской области – ответственный секретарь территориальной комиссии Сухоложского района по делам несовершеннолетних и защите их прав признан не состоявшимся.

 

Условия конкурса на замещение вакантных должностей ФГГС

В соответствии со статьей 21 Федерального закона Российской Федерации от 27.07.2004 № 79-ФЗ «О государственной гражданской службе Российской Федерации» на гражданскую службу вправе поступать граждане Российской Федерации, достигшие возраста 18 лет, владеющие государственным языком Российской Федерации и соответствующие квалификационным требованиям, установленным настоящим Федеральным законом.

 

Поступление на гражданскую службу и замещение должности гражданской службы по конкурсу

 

1. Поступление гражданина на гражданскую службу для замещения должности гражданской службы или замещение гражданским служащим другой должности гражданской службы осуществляется по результатам конкурса, если иное не установлено настоящей статьей. Конкурс заключается в оценке профессионального уровня претендентов на замещение должности гражданской службы, их соответствия установленным квалификационным требованиям для замещения должности гражданской службы.

2. Конкурс не проводится:

1) при назначении на замещаемые на определенный срок полномочий должности гражданской службы категорий «руководители» и «помощники (советники)»;

2) при назначении на должности гражданской службы категории «руководители», назначение на которые и освобождение от которых осуществляются Президентом Российской Федерации или Правительством Российской Федерации;

3) при заключении срочного служебного контракта;

4) при назначении гражданского служащего на иную должность гражданской службы в случаях, предусмотренных частью 2 статьи 28, частью 1 статьи 31 и частью 9 статьи 60. 1 Федерального закона Российской Федерации от 27.07.2004 № 79-ФЗ;

5) при назначении на должность гражданской службы гражданского служащего (гражданина), включенного в кадровый резерв на гражданской службе.

3. Конкурс может не проводиться при назначении на отдельные должности гражданской службы, исполнение должностных обязанностей по которым связано с использованием сведений, составляющих государственную тайну, по перечню должностей, утверждаемому нормативным актом государственного органа.

4. По решению представителя нанимателя конкурс может не проводиться при назначении на должности гражданской службы, относящиеся к группе младших должностей гражданской службы.

5. Претенденту на замещение должности гражданской службы может быть отказано в допуске к участию в конкурсе в связи с несоответствием квалификационным требованиям к вакантной должности гражданской службы, а также в связи с ограничениями, установленными Федеральным законом Российской Федерации от 27.07.2004 № 79-ФЗ для поступления на гражданскую службу и ее прохождения.

6. Претендент на замещение должности гражданской службы, не допущенный к участию в конкурсе, вправе обжаловать это решение в соответствии с Федеральным законом Российской Федерации от 27.07.2004 № 79-ФЗ.

7. Для проведения конкурса на замещение вакантной должности гражданской службы правовым актом соответствующего государственного органа образуется конкурсная комиссия.

8. В состав конкурсной комиссии входят представитель нанимателя и (или) уполномоченные им гражданские служащие (в том числе из подразделения по вопросам государственной службы и кадров, юридического (правового) подразделения и подразделения, в котором проводится конкурс на замещение вакантной должности гражданской службы), представитель соответствующего органа по управлению государственной службой, а также представители научных и образовательных организаций, других организаций, приглашаемые органом по управлению государственной службой по запросу представителя нанимателя в качестве независимых экспертов — специалистов по вопросам, связанным с гражданской службой, без указания персональных данных экспертов. Число независимых экспертов должно составлять не менее одной четверти от общего числа членов конкурсной комиссии.

8.1. В состав конкурсной комиссии в федеральном органе исполнительной власти, при котором в соответствии со статьей 20 Федерального закона от 4 апреля 2005 года N 32-ФЗ «Об Общественной палате Российской Федерации» образован общественный совет, а также в органе исполнительной власти субъекта Российской Федерации, при котором в соответствии с нормативным правовым актом субъекта Российской Федерации образован общественный совет, наряду с лицами, указанными в части 8 настоящей статьи, включаются представители указанных общественных советов. Общее число этих представителей и независимых экспертов должно составлять не менее одной четверти от общего числа членов конкурсной комиссии.

9. Состав конкурсной комиссии для проведения конкурса на замещение вакантной должности гражданской службы, исполнение должностных обязанностей по которой связано с использованием сведений, составляющих государственную тайну, формируется с учетом положений законодательства Российской Федерации о государственной тайне.

10. Состав конкурсной комиссии формируется таким образом, чтобы была исключена возможность возникновения конфликтов интересов, которые могли бы повлиять на принимаемые конкурсной комиссией решения.

11. Претендент на замещение должности гражданской службы вправе обжаловать решение конкурсной комиссии в соответствии с Федеральным законом Российской Федерации от 27.07.2004 № 79-ФЗ.

12. Положение о конкурсе на замещение вакантной должности государственной гражданской службы Российской Федерации, определяющее порядок и условия его проведения, утверждается указом Президента Российской Федерации.

 На текущий момент времени вакансии на замещение должностей федеральных государственных гражданских служащих в ОМВД России по городскому округу Луховицы отсутствуют.

Конкурсы на замещение вакантных должностей

Филиал «Восход» МАИ объявляет конкурс на замещение должности старшего преподавателя по кафедре:

• «Вычислительные системы и технологии»

Срок подачи заявлений не позднее месяца со дня публикации объявления.
Телефон для справок: 51601

07.09.2020 г.

---

Филиал «Восход» МАИ объявляет конкурс на замещение должностей профессорско-преподавательского состава по кафедрам:

• «Конструкция и испытания летательных аппаратов» – ассистент, старший преподаватель;
• «Вычислительные системы и технологии» – доцент.

Срок подачи заявлений не позднее месяца со дня публикации объявления.
Телефон для справок: 51601

09.04.2020 г.

---

Филиал «Восход» МАИ объявляет конкурс на замещение должностей профессорско-преподавательского состава по кафедрам:

• Экономика и менеджмент – старший преподаватель, доцент;
• Математическое и программное обеспечение информационных систем – доцент.

Срок подачи заявлений не позднее месяца со дня публикации объявления.
Телефон для справок: 51601

05.03.2020 г.

---

Филиал «Восход» МАИ объявляет конкурс на замещение должности старшего преподавателя по кафедре

• Б11 – Конструкция и испытания летательных аппаратов

Срок подачи заявлений не позднее месяца со дня публикации объявления.
Телефон для справок: 51601

20.11.2019 г.

---

Филиал «Восход» МАИ объявляет конкурс на замещение должности доцента по кафедре

• Б11 – Конструкция и испытания летательных аппаратов

Срок подачи заявлений не позднее месяца со дня публикации объявления.
Телефон для справок: 51601

04.04.2019 г.

---

Филиал «Восход» МАИ объявляет конкурс на замещение должностей профессорско-преподавательского состава по кафедрам:

• Б11 – Конструкция и испытания летательных аппаратов – старший преподаватель, доцент;
• Б12 – Экономика и менеджмент – старший преподаватель;
• Б21 – Вычислительные системы и технологии – старший преподаватель.

Срок подачи заявлений не позднее месяца со дня публикации объявления.
Телефон для справок: 51601

18.04.2018 г.

---

Замещение активов в банкротстве: самое актуальное

Предстоящее мероприятие

Предстоящее мероприятие

Замещение активов в банкротстве: самое актуальное

Вебинар юридической компании «РКТ» при поддержке ИД «Коммерсантъ»

25 марта 2021

Одной из мер по восстановлению платежеспособности должника в ходе внешнего управления и конкурсного производства, а также альтернативой стандартной продажи имущества через торги является процедура замещения активов. Сегодня данный механизм является довольно актуальным для компаний, которые хотят начать вести бизнес «с чистого листа». Однако нормативное регулирование замещения активов имеет ряд пробелов и противоречий, которые были выявлены судебной практикой, в частности, по вопросам прав залоговых кредиторов при замещении активов, передачи нематериальных активов и обязательств должника вновь созданному в результате замещения активов обществу или обществам. При этом, как и многие институты банкротства, замещение активов подвержено множеству форм и видов злоупотреблений со стороны недобросовестных участников банкротства, использующих замещение активов с противоправными целями. 

Регистрация по ссылке: https://events.webinar.ru/rct/8350225

Вопросы для обсуждения:

• В чем ценность данного способа пополнения конкурсной массы? 

• Замещение активов и права залоговых кредиторов

• Особенности внесения имущества в уставный капитал. Передача нематериальных активов

• Передача обязательств должника создаваемому акционерному обществу: когда это возможно? 

• Управление созданным акционерным обществом: возможности и ограничения

• Злоупотребления при замещении активов. 

Объявление о выборах на замещение должностей профессорско-преподавательского состава

ФГБОУ ВО «Ухтинский государственный технический университет» объявляет ВЫБОРЫ на замещение должности профессорско-преподавательского состава по кафедре:

• Механики – заведующий кафедрой – 1.

Срок подачи заявления на выборы не позднее месяца со дня опубликования объявления.

Претенденты, не работающие в университете, к заявлению прилагают: личный листок по учету кадров с фотографией, заверенный кадровой службой по месту работы; автобиографию; заверенные копии дипломов о высшем образовании, ученой степени и аттестата об ученом звании; список опубликованных учебных изданий и научных трудов, подписанный соискателем и заверенный по месту работы, характеристика с места работы.

Работающие в университете подают заявление и список опубликованных учебных изданий и научных трудов.

Кандидаты на должность заведующего кафедрой должны соответствовать установленным нормативным актам, квалификационным и иным требованиям. В случае несоответствия установленным требованиям и (или) нарушения сроков предоставления необходимых документов кандидату может быть отказано в допуске к участию в выборах.

Требования, предъявляемые к должности заведующего кафедрой в соответствии с Единым квалификационным справочником должностей руководителей, специалистов и служащих, раздел «Квалификационные характеристики должностей руководителей и специалистов высшего профессионального и дополнительного профессионального образования», утвержденным приказом Минздравсоцразвития РФ от 11. 01.2011 № 1н: высшее образование, наличие ученой степени и ученого звания, стаж научно-педагогической работы или работы в организациях по направлению профессиональной деятельности кафедры, не менее 5 лет.

По всем вопросам (порядок и условия проведения конкурса, место, дата, результаты, № протоколов) обращаться к ученому секретарю  каб. 309 корп. «А», 304 корп. «Б», тел.: 77-44-11.

Порядок обжалования результатов конкурса на замещение вакантных должностей государственной гражданской службы

В соответствии со статьей 27 Положения о конкурсе на замещение вакантной должности государственной гражданской службы Российской Федерации, утвержденного Указом Президента Российской Федерации от 01 февраля 2005 года № 112 «О конкурсе на замещение вакантной должности государственной гражданской службы Российской Федерации» кандидат на замещение вакантной должности государственной гражданской службы вправе обжаловать решение конкурсной комиссии в соответствии с законодательством Российской Федерации.

Порядок обжалования результатов конкурсов на замещение вакантных должностей государственной гражданской службы установлен Федеральным законом от 27 июля 2004 года № 79-ФЗ «О государственной гражданской службе Российской Федерации».

Согласно статьям 69 и 70 Федерального закона от 27 июля 2004 г. № 79-ФЗ «О государственной гражданской службе Российской Федерации» (далее – Федеральный закон) неурегулированные между представителем нанимателя и гражданским служащим либо гражданином, поступающим на гражданскую службу или ранее состоявшим на гражданской службе, разногласия (далее – индивидуальный служебный спор) по вопросам применения законов, иных нормативных правовых актов о гражданской службе и служебного контракта, рассматриваются следующими органами по рассмотрению индивидуальных служебных споров (далее — органы по рассмотрению служебных споров):

— комиссией государственного органа по служебным спорам;

— судом.

Порядок рассмотрения служебных споров в органах по рассмотрению служебных споров регулируется Федеральным законом и другими федеральными законами, а порядок рассмотрения дел по служебным спорам в судах определяется также гражданским процессуальным законодательством Российской Федерации.

Комиссия государственного органа по служебным спорам (далее — комиссия по служебным спорам) образуется решением представителя нанимателя из равного числа представителей выборного профсоюзного органа данного государственного органа и представителя нанимателя.

Представители выборного профсоюзного органа данного государственного органа избираются в комиссию по служебным спорам на конференции гражданских служащих государственного органа. Представители представителя нанимателя назначаются в комиссию по служебным спорам представителем нанимателя.

Служебный спор рассматривается комиссией по служебным спорам в случае, если гражданский служащий самостоятельно или с участием своего представителя не урегулировал разногласия при непосредственных переговорах с представителем нанимателя.

Гражданский служащий либо гражданин, поступающий на гражданскую службу или ранее состоявший на гражданской службе, может обратиться в комиссию по служебным спорам в трехмесячный срок со дня, когда он узнал или должен был узнать о нарушении своего права.

В случае пропуска по уважительным причинам установленного действующим законодательством Российской Федерации срока комиссия по служебным спорам может восстановить этот срок и рассмотреть служебный спор по существу. Поступившее в комиссию по служебным спорам письменное заявление гражданского служащего либо гражданина, поступающего на гражданскую службу или ранее состоявшего на гражданской службе, подлежит обязательной регистрации указанной комиссией в день его подачи.

Комиссия по служебным спорам обязана рассмотреть служебный спор в течение десяти календарных дней со дня подачи письменного заявления.

Порядок рассмотрения служебного спора комиссией по служебным спорам, а также порядок принятия решения комиссией по служебным спорам и его исполнения регулируется законодательством Российской Федерации.

Решение комиссии по служебным спорам может быть обжаловано любой из сторон в суд в десятидневный срок со дня вручения ей копии решения комиссии. В случае пропуска по уважительным причинам установленного срока суд может восстановить этот срок и рассмотреть служебный спор по существу.

В судах рассматриваются служебные споры по письменным заявлениям гражданского служащего либо гражданина, поступающего на гражданскую службу или ранее состоявшего на гражданской службе, представителя нанимателя или представителя выборного профсоюзного органа данного государственного органа, если хотя бы один из них не согласен с решением комиссии по служебным спорам либо если гражданский служащий или представитель нанимателя обращается в суд без обращения в комиссию по служебным спорам, а также по заявлению прокурора, если решение комиссии по служебным спорам не соответствует федеральным законам или иным нормативным правовым актам Российской Федерации.

Заявление подается в суд по подсудности, установленной статьями 24-27 Гражданского процессуального кодекса Российской Федерации, по месту его жительства или по месту нахождения органа государственной власти, органа местного самоуправления, должностного лица, государственного или муниципального служащего, решение, действие (бездействие) которых оспариваются.

Замена

«Заменить» означает поставить на место другого.

Замена

В алгебре «подстановка» означает ввод цифр вместо букв:

	Когда у нас будет:
	А мы знаем, что x = 6 …
	… тогда мы можем «заменить» 6 на x :

Пример: когда x = 2, что составляет

10 / x + 4 ?

Укажите «2», где «x» равно:

.

10/2 + 4 = 5 + 4 = 9

Пример: когда x = 5, что такое

x + x / 2 ?

Укажите «5», где «x» равно:

.

5 + 5/2 = 5 + 2. 5 = 7,5

Пример: если x = 3 и y = 4, то что такое

x ² + xy ?

Поместите «3», где «x» — это, и «4», где «y» — это:

3 ² + 3 × 4 = 3 × 3 + 12 = 21

Пример: Если x = 3 (но мы не знаем «y»), то что такое

x ² + xy ?

Укажите «3», где «x» равно:

.

3 ² + 3y = 9 + 3y

(то есть насколько мы можем достать)

Как показал последний пример, мы не всегда можем получить число для ответа, иногда просто более простую формулу.

Отрицательные числа

При замене отрицательных чисел заключите их в (), чтобы произвести правильные вычисления.

Пример: Если x =

−2 , то что такое 1 — x + x ² ?

Положите «(−2)», где «x» равно:

.

1 — (−2) + (−2) ² = 1 + 2 + 4 = 7

В последнем примере:

• — (−2) стало +2
• (−2) ² стало +4

из-за этих особых правил:

	Правило	Сложение или Вычитание		Умножение или Деление
	Два одинаковых знака превращаются в знак положительный	3 + (+ 2) = 3 + 2 = 5		3 × 2 = 6
		6 — (- 3) = 6 + 3 = 9		(−3) × (−2) = 6
	Два непохожих знака превращаются в знак минуса	7 + (- 2) = 7 — 2 = 5		3 × (−2) = −6
		8 — (+ 2) = 8 — 2 = 6		(−3) × 2 = −6

Определение замены по Merriam-Webster

подписка | \ ˌSəb-stə-ˈtü-shən , -ˈTyü- \ 1а : действие, процесс или результат замены одного объекта другим.

б : замена одной математической сущности другой равной ценности

Методы замены и добавления

Результаты обучения

• Используйте метод подстановки, чтобы найти решение (я) системы двух линейных уравнений.
• Используйте метод сложения, чтобы найти решение (я) системы линейных уравнений.

Решение систем уравнений подстановкой

Решение линейной системы с двумя переменными с помощью построения графиков хорошо работает, когда решение состоит из целых значений, но если наше решение содержит десятичные дроби или дроби, это не самый точный метод. Мы рассмотрим еще два метода решения системы линейных уравнений , которые более точны, чем построение графиков. Одним из таких методов является решение системы уравнений методом подстановки , в котором мы решаем одно из уравнений для одной переменной, а затем подставляем результат во второе уравнение, чтобы найти вторую переменную.Напомним, что мы можем решать только одну переменную за раз, поэтому метод подстановки является одновременно ценным и практичным.

Как: дана система двух уравнений с двумя переменными, решите, используя метод подстановки.

1. Решите одно из двух уравнений относительно одной из переменных через другую.
2. Подставьте выражение для этой переменной во второе уравнение, затем найдите оставшуюся переменную.
3. Подставьте это решение в любое из исходных уравнений, чтобы найти значение первой переменной.Если возможно, запишите решение в виде упорядоченной пары.
4. Проверьте решение в обоих уравнениях.

Пример: решение системы уравнений с двумя переменными подстановкой

Решите следующую систему уравнений путем подстановки.

[латекс] \ begin {align} -x + y & = — 5 \\ 2x-5y & = 1 \ end {align} [/ latex]

Показать решение

Сначала мы решим первое уравнение для [латекс] y [/ латекс].

[латекс] \ begin {align} -x + y & = — 5 \\ y & = x — 5 \ end {align} [/ latex]

Теперь мы можем заменить выражение [latex] x — 5 [/ latex] на [latex] y [/ latex] во втором уравнении.

[латекс] \ begin {align} 2x — 5y & = 1 \\ 2x — 5 \ left (x — 5 \ right) & = 1 \\ 2x — 5x + 25 & = 1 \\ -3x & = — 24 \\ x & = 8 \ end {align} [/ latex]

Теперь мы подставляем [latex] x = 8 [/ latex] в первое уравнение и решаем относительно [latex] y [/ latex].

[латекс] \ begin {align} — \ left (8 \ right) + y & = — 5 \\ y & = 3 \ end {align} [/ latex]

Наше решение — [латекс] \ left (8,3 \ right) [/ latex].

Проверьте решение, подставив [latex] \ left (8,3 \ right) [/ latex] в оба уравнения.

[латекс] \ begin {align} -x + y & = — 5 \\ — \ left (8 \ right) + \ left (3 \ right) & = — 5 && \ text {True} \\ [3mm] 2x — 5y & = 1 \\ 2 \ left (8 \ right) -5 \ left (3 \ right) & = 1 && \ text {True} \ end {align} [/ latex]

Попробуйте

Вы можете использовать онлайн-инструмент построения графиков, который поможет вам решить систему уравнений путем подстановки. Мы будем использовать следующую систему, чтобы показать вам, как:

[латекс] \ begin {align} x & = y + 3 \\ 4 & = 3x — 2y \ end {align} [/ latex]

Сначала решите оба уравнения относительно y:

[латекс] \ begin {align} y & = x-3 \\ y & = \ frac {3} {2} x — 2 \ end {align} [/ latex]

Теперь введите [latex] x-3 = \ frac {3} {2} x — 2 [/ latex] в Desmos.Вы увидите, что Desmos предоставил вам [латекс] x = -2 [/ latex].

Теперь вы можете заменить [latex] x = -2 [/ latex] в оба уравнения. Если вы получите одинаковый результат для обоих, вы нашли решение для упорядоченной пары. Попробуйте.

Показать решение

[латекс] \ влево (-2, -5 \ вправо) [/ латекс]

Вопросы и ответы

Можно ли методом подстановки решить любую линейную систему с двумя переменными?

Да, но этот метод работает лучше всего, если одно из уравнений содержит коэффициент 1 или –1, чтобы нам не приходилось иметь дело с дробями.

Следующее видео длится ~ 10 минут и представляет собой мини-урок по использованию метода подстановки для решения системы линейных уравнений. Мы представляем три разных примера, а также используем инструмент построения графиков, чтобы подытожить решение для каждого примера.

Решение систем уравнений с двумя переменными методом сложения

Третий метод решения систем линейных уравнений — это метод сложения , этот метод также называется методом исключения . В этом методе мы складываем два члена с одинаковой переменной, но с противоположными коэффициентами, так что сумма равна нулю. Конечно, не все системы созданы с двумя членами одной переменной, имеющими противоположные коэффициенты. Часто нам приходится корректировать одно или оба уравнения умножением, чтобы одна переменная была исключена сложением.

Как: решить систему уравнений методом сложения.

1. Запишите оба уравнения с переменными x и y слева от знака равенства и константами справа.
2. Напишите одно уравнение над другим, выстроив соответствующие переменные. Если одна из переменных в верхнем уравнении имеет коэффициент, противоположный той же переменной в нижнем уравнении, сложите уравнения вместе, исключив одну переменную. Если нет, используйте умножение на ненулевое число, чтобы одна из переменных в верхнем уравнении имела коэффициент, противоположный той же переменной в нижнем уравнении, затем добавьте уравнения, чтобы исключить переменную.
3. Решите полученное уравнение для оставшейся переменной.
4. Подставьте это значение в одно из исходных уравнений и решите для второй переменной.
5. Проверьте решение, подставив значения в другое уравнение.

Пример: решение системы методом сложения

Решите данную систему уравнений сложением.

[латекс] \ begin {align} x + 2y & = — 1 \\ -x + y & = 3 \ end {align} [/ latex]

Показать решение

Оба уравнения уже установлены равными константе. Обратите внимание, что коэффициент [латекс] x [/ латекс] во втором уравнении, –1, противоположен коэффициенту [латекс] x [/ латекс] в первом уравнении, 1.Мы можем сложить два уравнения, чтобы исключить [latex] x [/ latex] без умножения на константу.

[латекс] \ begin {align} x + 2y & = — 1 \\ -x + y & = 3 \\ \ hline 3y & = 2 \ end {align} [/ latex]

Теперь, когда мы удалили [latex] x [/ latex], мы можем решить полученное уравнение для [latex] y [/ latex].

[латекс] \ begin {align} 3y & = 2 \\ y & = \ dfrac {2} {3} \ end {align} [/ latex]

Затем мы подставляем это значение для [latex] y [/ latex] в одно из исходных уравнений и решаем для [latex] x [/ latex].

[латекс] \ begin {align} -x + y & = 3 \\ -x + \ frac {2} {3} & = 3 \\ -x & = 3- \ frac {2} {3} \\ -x & = \ frac {7} {3} \\ x & = — \ frac {7} {3} \ end {align} [/ latex]

Решение этой системы — [латекс] \ left (- \ frac {7} {3}, \ frac {2} {3} \ right) [/ latex].

Проверьте решение в первом уравнении.

[латекс] \ begin {align} x + 2y & = — 1 \\ \ left (- \ frac {7} {3} \ right) +2 \ left (\ frac {2} {3} \ right) & = \\ — \ frac {7} {3} + \ frac {4} {3} & = \\ — \ frac {3} {3} & = \\ -1 & = — 1 && \ text {True} \ end { align} [/ латекс]

Анализ решения

Мы получаем важное представление о системах уравнений, глядя на графическое представление.Посмотрите на график ниже, чтобы увидеть, что уравнения пересекаются в решении. Нам не нужно спрашивать, может ли быть второе решение, потому что наблюдение за графиком подтверждает, что система имеет ровно одно решение.

Пример: использование метода сложения, когда требуется умножение одного уравнения

Решите данную систему уравнений методом сложения .

[латекс] \ begin {align} 3x + 5y & = — 11 \\ x — 2y & = 11 \ end {align} [/ latex]

Показать решение

Добавление этих уравнений в представленном виде не устраняет переменную.Однако мы видим, что в первом уравнении есть [latex] 3x [/ latex], а во втором уравнении — [latex] x [/ latex]. Итак, если мы умножим второе уравнение на [latex] -3, \ text {} [/ latex], элементы x прибавятся к нулю.

[латекс] \ begin {align} x — 2y & = 11 \\ -3 \ left (x — 2y \ right) & = — 3 \ left (11 \ right) && \ text {Умножаем обе стороны на} -3 \ \ -3x + 6y & = — 33 && \ text {Использовать свойство распределения}. \ end {align} [/ latex]

А теперь добавим их.

[латекс] \ begin {align} 3x + 5y & = — 11 \\ −3x + 6y & = — 33 \\ \ hline 11y & = — 44 \\ y & = — 4 \ end {align} [/ latex]

На последнем этапе мы подставляем [latex] y = -4 [/ latex] в одно из исходных уравнений и решаем для [latex] x [/ latex].

[латекс] \ begin {align} 3x + 5y & = — 11 \\ 3x + 5 \ left (-4 \ right) & = — 11 \\ 3x — 20 & = — 11 \\ 3x & = 9 \\ x & = 3 \ end {align} [/ latex]

Наше решение — упорядоченная пара [латекс] \ left (3, -4 \ right) [/ latex]. Проверьте решение в исходном втором уравнении.

[латекс] \ begin {align} x — 2y & = 11 \\ \ left (3 \ right) -2 \ left (-4 \ right) & = 3 + 8 \\ & = 11 && \ text {True} \ конец {align} [/ latex]

Попробуйте

Решите систему уравнений сложением.

[латекс] \ begin {align} 2x — 7y & = 2 \\ 3x + y & = — 20 \ end {align} [/ latex]

Показать решение

[латекс] \ влево (-6, -2 \ вправо) [/ латекс]

Пример: использование метода сложения, когда требуется умножение обоих уравнений

Решите данную систему уравнений с двумя переменными сложением.

[латекс] \ begin {align} 2x + 3y & = — 16 \\ 5x — 10y & = 30 \ end {align} [/ latex]

Показать решение

Одно уравнение имеет [латекс] 2x [/ латекс], а другое — [латекс] 5x [/ латекс].Наименьшее общее кратное — [latex] 10x [/ latex], поэтому нам придется умножить оба уравнения на константу, чтобы исключить одну переменную. Давайте удалим [latex] x [/ latex], умножив первое уравнение на [latex] -5 [/ latex], а второе уравнение на [latex] 2 [/ latex].

[латекс] \ begin {align} -5 \ left (2x + 3y \ right) & = — 5 \ left (-16 \ right) \\ -10x — 15y & = 80 \\ [3 мм] 2 \ left (5x — 10y \ right) & = 2 \ left (30 \ right) \\ 10x — 20y & = 60 \ end {align} [/ latex]

Затем мы складываем два уравнения.

[латекс] \ begin {align} -10x-15y & = 80 \\ 10x-20y & = 60 \\ \ hline -35y & = 140 \\ y & = — 4 \ end {align} [/ latex]

Подставьте [латекс] y = -4 [/ latex] в исходное первое уравнение.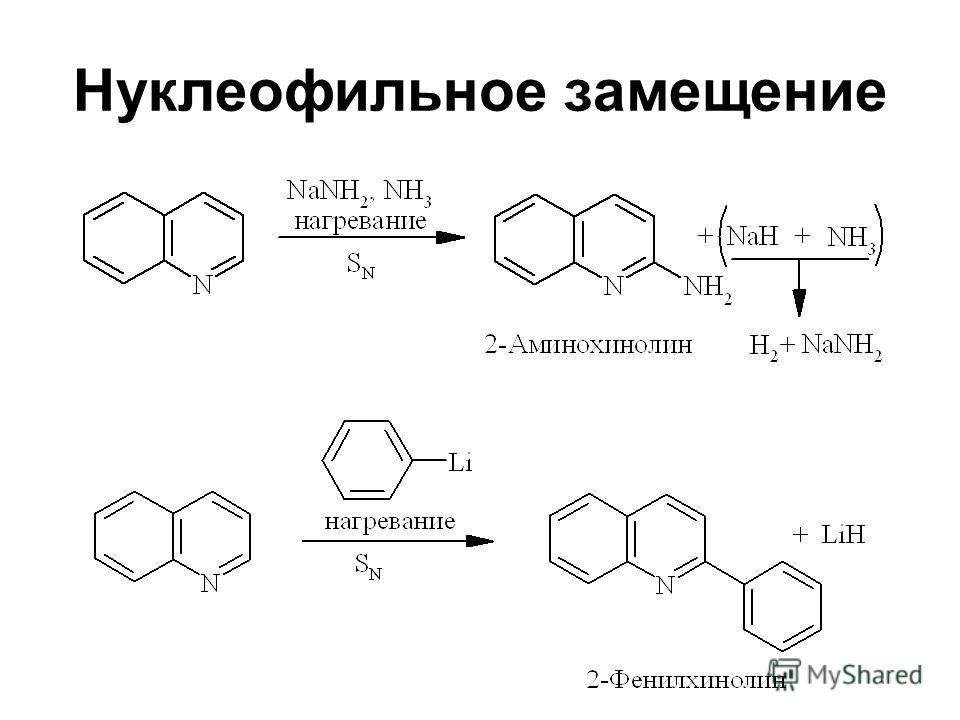

[латекс] \ begin {align} 2x + 3 \ left (-4 \ right) & = — 16 \\ 2x — 12 & = — 16 \\ 2x & = — 4 \\ x & = — 2 \ end {align} [ / латекс]

Решение: [латекс] \ left (-2, -4 \ right) [/ latex]. Проверьте это в другом уравнении.

[латекс] \ begin {align} 5x — 10y & = 30 \\ 5 \ left (-2 \ right) -10 \ left (-4 \ right) & = 30 \\ -10 + 40 & = 30 \\ 30 & = 30 \ end {align} [/ latex]

Пример: использование метода сложения в системах уравнений, содержащих дроби

Решите данную систему уравнений с двумя переменными сложением.

[латекс] \ begin {align} \ frac {x} {3} + \ frac {y} {6} & = 3 \\ [1 мм] \ frac {x} {2} — \ frac {y} {4 } & = 1 \ end {align} [/ latex]

Показать решение

Сначала очистите каждое уравнение от дробей, умножив обе части уравнения на наименьший общий знаменатель.

[латекс] \ begin {align} 6 \ left (\ frac {x} {3} + \ frac {y} {6} \ right) & = 6 \ left (3 \ right) \\ [1 мм] 2x + y & = 18 \\ [3 мм] 4 \ left (\ frac {x} {2} — \ frac {y} {4} \ right) & = 4 \ left (1 \ right) \\ [1 мм] 2x-y & = 4 \ end {align} [/ latex]

Теперь умножьте второе уравнение на [latex] -1 [/ latex], чтобы мы могли исключить x .

[латекс] \ begin {align} -1 \ left (2x-y \ right) & = — 1 \ left (4 \ right) \\ [1 мм] -2x + y & = — 4 \ end {align} [/ латекс]

Сложите два уравнения, чтобы исключить x , и решите полученное уравнение относительно y .

[латекс] \ begin {align} 2x + y & = 18 \\ −2x + y & = — 4 \\ \ hline 2y & = 14 \\ y & = 7 \ end {align} [/ latex]

Подставьте [латекс] y = 7 [/ латекс] в первое уравнение.

[латекс] \ begin {align} 2x + \ left (7 \ right) & = 18 \\ 2x & = 11 \\ x & = \ frac {11} {2} \\ & = 7.5 \ end {align} [/ latex]

Решение: [латекс] \ left (\ frac {11} {2}, 7 \ right) [/ latex]. Проверьте это в другом уравнении.

[латекс] \ begin {align} \ frac {x} {2} — \ frac {y} {4} & = 1 \\ [1 мм] \ frac {\ frac {11} {2}} {2} — \ frac {7} {4} & = 1 \\ [1 мм] \ frac {11} {4} — \ frac {7} {4} & = 1 \\ [1 мм] \ frac {4} {4} & = 1 \ end {align} [/ latex]

Попробуйте

Решите систему уравнений сложением.

[латекс] \ begin {align} 2x + 3y & = 8 \\ 3x + 5y & = 10 \ end {align} [/ latex]

Показать решение

[латекс] \ влево (10, -4 \ вправо) [/ латекс]

в следующем видео мы представляем больше примеров того, как использовать метод сложения (исключения) для решения системы двух линейных уравнений.

Внесите свой вклад!

У вас была идея улучшить этот контент? Нам очень понравится ваш вклад.

Улучшить эту страницуПодробнее

Исчисление I — Правило замещения неопределенных интегралов

Показать мобильное уведомление Показать все заметки Скрыть все заметки

Похоже, вы используете устройство с «узкой» шириной экрана ( i.е. вы, вероятно, пользуетесь мобильным телефоном). Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в альбомном режиме, многие уравнения будут отображаться сбоку от вашего устройства (вы сможете прокручивать их, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана.

Раздел 5-3: Правило замещения неопределенных интегралов

После последнего раздела мы теперь знаем, как делать следующие интегралы.{\ frac {5} {4}}} + c \]

Как всегда, мы можем проверить наш ответ с помощью быстрой производной, если мы хотим, и не забыть «обратную замену» и вернуть интеграл в виде исходной переменной.

То, что мы сделали в вышеупомянутой работе, называется правилом замены .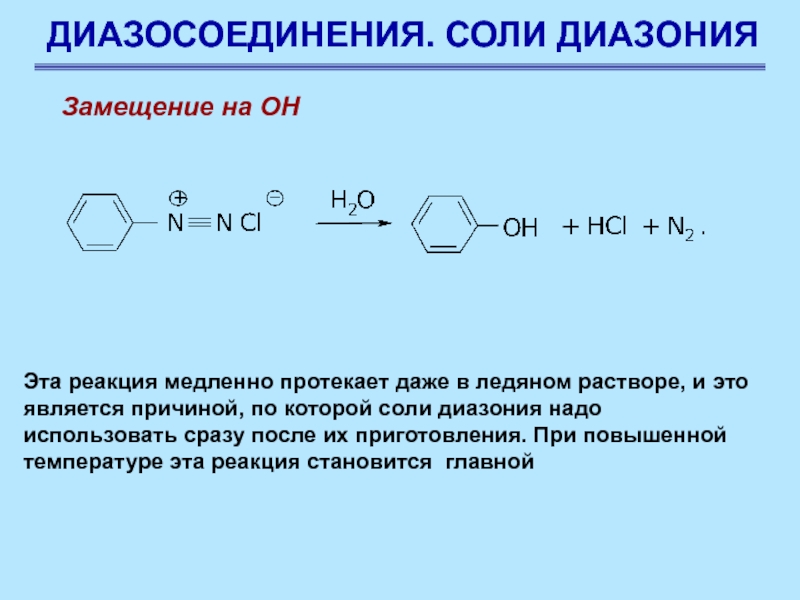 Вот общее правило подстановки.

Правило замещения

\ [\ int {{f \ left ({g \ left (x \ right)} \ right) \, g ‘\ left (x \ right) \, dx}} = \ int {{f \ left (u \ справа) \, du}}, \ hspace {0.25in} {\ mbox {где,}} u = g \ left (x \ right) \]

Естественный вопрос на этом этапе — как определить правильную замену. К сожалению, ответ зависит от интеграла. Однако есть общее практическое правило, которое будет работать для многих интегралов, которые мы собираемся использовать.

Столкнувшись с интегралом, мы спросим себя, что мы умеем интегрировать. С помощью приведенного выше интеграла мы можем быстро понять, что знаем, как интегрировать

\ [\ int {{\ sqrt [4] {x} \, dx}} \]

Однако у нас не было только корня, у нас также были вещи перед корнем и (что более важно в данном случае) вещи под корнем.Поскольку мы можем интегрировать корни только в том случае, если под корнем есть только \ (x \), хорошее первое предположение для замены состоит в том, чтобы сделать \ (u \) материалом под корнем.

Другой способ подумать об этом — спросить себя, должны ли вы дифференцировать подынтегральное выражение (мы не, конечно, но только на секунду притворимся, что были), существует ли цепное правило и какова внутренняя функция для цепочки правило. Если существует цепное правило (для производной), то весьма вероятно, что внутренняя функция будет заменой, которая позволит нам выполнить интеграл.

Однако мы должны быть осторожны. Бывают случаи, когда использование этого общего правила может доставить нам неприятности или чрезмерно усложнить проблему. В конечном итоге мы столкнемся с проблемами, когда существует несколько «внутренних функций» и / или интегралов, которые будут выглядеть очень похожими, но при этом будут использовать совершенно разные замены. Реальность такова, что единственный способ действительно научиться делать замены — это просто работать над множеством задач, и в конечном итоге вы начнете понимать, как они работают, и вам будет легче и легче определять правильные замены.

Теперь, разобравшись с этим, мы должны задать следующий вопрос. Как мы узнаем, правильно ли мы получили замену? Итак, после вычисления дифференциала и фактического выполнения замены каждый \ (x \) в интеграле (включая \ (x \) в \ (dx \)) должен исчезнуть в процессе замены, и единственные оставшиеся буквы должны быть \ (u \) (включая a \ (du \)), и мы должны остаться с интегралом, который мы можем сделать.

Если остались \ (x \) или у нас есть интеграл, который невозможно вычислить, то есть довольно хороший шанс, что мы выбрали неправильную замену.К сожалению, есть по крайней мере один случай (мы увидим пример этого в следующем разделе), когда при правильной замене на самом деле останется несколько \ (x \), и нам нужно будет проделать немного больше работы. чтобы заставить его работать.

Опять же, здесь невозможно переоценить, что единственный способ действительно научиться делать замены — это просто работать над множеством задач. Существует множество различных типов проблем, и после решения многих проблем вы начнете по-настоящему почувствовать эти проблемы, и после того, как вы проработаете их достаточно, вы достигнете точки, когда вы сможете выполнять простые замены в своем голову без необходимости фактически ничего записывать.

В качестве заключительного примечания мы должны указать, что часто (фактически почти в каждом случае) дифференциал не отображается точно в подынтегральном выражении, как в приведенном выше примере, и иногда нам нужно выполнить некоторые манипуляции с подынтегральным выражением и / или дифференциал, чтобы все \ (x \) исчезли при замене.

Давайте поработаем несколько примеров, чтобы лучше понять, как работает правило подстановки.

Пример 1 Вычислите каждый из следующих интегралов.2}}}} \, dx}} \) Показать все решения Скрыть все решения a \ (\ displaystyle \ int {{\ left ({1 — \ frac {1} {w}} \ right) \ cos \ left ({w — \ ln w} \ right) \, dw}} \) Показать Решение

В этом случае похоже, что у нас есть косинус с внутренней функцией, поэтому давайте воспользуемся этим в качестве замены.

\ [u = w — \ ln w \ hspace {0,5 дюйма} du = \ left ({1 — \ frac {1} {w}} \ right) dw \]

Итак, как и в первом примере, мы работали с косинусом точно в дифференциале.{\ frac {1} {2}}} + c \ end {align *} \]

В предыдущем наборе примеров подстановка была в целом довольно ясной. Был ровно один термин, у которого была «внутренняя функция», и поэтому вариантов для замены было немного. Давайте рассмотрим несколько более сложных задач, чтобы убедиться, что мы не ожидаем, что все замены будут такими же, как в предыдущем наборе примеров.

Пример 2 Вычислите каждый из следующих интегралов.4} \, dx}} \) Показать решение

В этой задаче две «внутренние функции». Есть \ (1 — x \), который находится внутри двух триггерных функций, а также есть член, который возведен в степень 4 ^th .

Есть два способа решить эту проблему. Первая идея, которая приходит в голову многим студентам, — это заменить \ (1 — x \). В этом нет ничего плохого, но это не устраняет проблему термина для мощности 4 ^th .Это все еще существует, и если бы мы использовали эту идею, нам нужно было бы сделать вторую замену, чтобы справиться с этим.

Второй (и гораздо более простой) способ решить эту проблему — просто разобраться с вещами, увеличенными до мощности 4 ^th , и посмотреть, что мы получим. Подстановка в этом случае будет:

. \ [u = 2 — \ cos \ left ({1 — x} \ right) \ hspace {0.25in} \, \, \, \, \, \, \, du = — \ sin \ left ({1 — x} \ right) dx \ hspace {0.5in} \ Rightarrow \ hspace {0.25in} \ sin \ left ({1 — x} \ right) dx = — du \]

Здесь следует отметить два момента. Во-первых, не забывайте правильно обращаться со знаком «-». Распространенная ошибка на этом этапе — потерять его. Во-вторых, обратите внимание, что \ (1 — x \) на самом деле не проблема. Поскольку \ (1 — x \) был «похоронен» в подстановке, которую мы фактически использовали, о нем также позаботились в то же время. 5} + c \ end {align *} \]

Как видно из этого примера, иногда может показаться, что необходимо выполнить две замены, однако, если одна из них находится внутри другой замены, нам действительно нужно будет сделать только одну.{10}} \]

Используя это, похоже, что правильная замена —

\ [u = \ sin \ left ({3z} \ right) \ hspace {0,5 дюйма} du = 3 \ cos \ left ({3z} \ right) dz \ hspace {0,25 дюйма} \ Rightarrow \ hspace {0,25 дюйма} \ cos \ left ({3z} \ right) dz = \ frac {1} {3} du \]

Обратите внимание, что у нас снова были две очевидные замены в этом интеграле, но снова 3 \ (z \) скрывается в замене, которую мы используем, и поэтому нам не нужно было об этом беспокоиться.

Вот интеграл.4} + c \ end {выровнять *} \]

Самое важное, что нужно помнить в задачах подстановки, — это то, что после подстановки все исходные переменные должны исчезнуть из интеграла. После подстановки единственными переменными, которые должны присутствовать в интеграле, должна быть новая переменная из подстановки (обычно \ (u \)). Также обратите внимание, что сюда входят переменные в дифференциале!

Следующий набор примеров, хотя и не особенно сложен, может вызвать проблемы, если мы не обращаем внимания на то, что делаем.2} + 4}} \, dy}} \) Показать все решения Скрыть все решения a \ (\ displaystyle \ int {{\ frac {3} {{5y + 4}} \, dy}} \) Показать решение

Мы еще не видели такой проблемы. Заметим, что если мы возьмем знаменатель и продифференцируем его, мы получим просто константу, и единственное, что у нас есть в числителе, также будет константой. Это довольно хороший признак того, что мы можем использовать знаменатель для нашей замены, так что

\ [u = 5y + 4 \ hspace {0.5in} du = 5 \, dy \ hspace {0,25in} \ Rightarrow \ hspace {0,25in} \, \, \, \, \, \, dy = \ frac {1} {5} du \]

Интеграл сейчас,

\ [\ begin {align *} \ int {{\ frac {3} {{5y + 4}} \, dy}} & = \ frac {3} {5} \ int {{\ frac {1} {u } \, du}} \\ & = \ frac {3} {5} \ ln \ left | и \ право | + c \\ & = \ frac {3} {5} \ ln \ left | {5y + 4} \ right | + c \ end {align *} \]

Помните, что мы можем просто вычленить 3 в числителе из интеграла, и это делает интеграл в данном случае более понятным.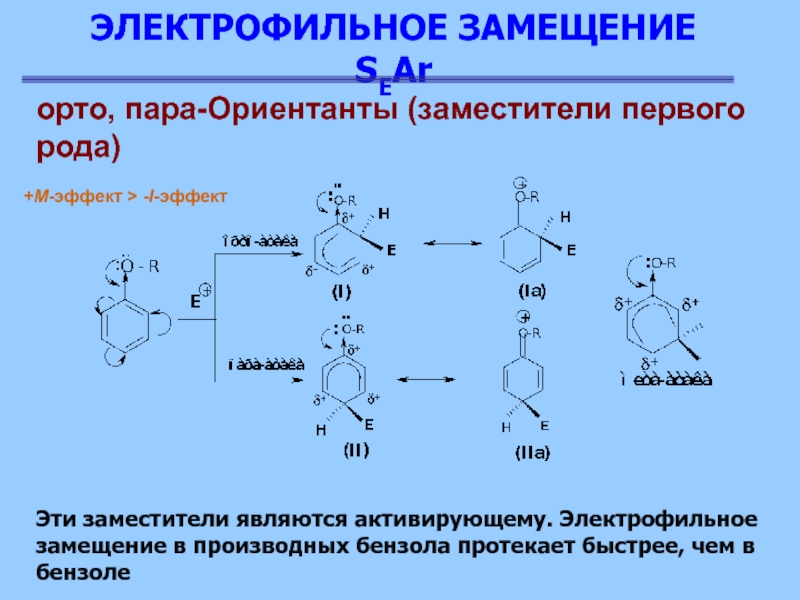 4} + 2t} \ right | + c \ end {align *} \]

Итак, в данном случае мы получаем логарифм от интеграла.{- 1}} \ left ({2x} \ right) + c \ end {align *} \]

Поскольку этот документ также представлен в Интернете, мы собираемся поместить остальные примеры правил подстановки в следующий раздел. Со всеми примерами в одном разделе этот раздел становился слишком большим для веб-презентации.

Решение линейных систем заменой

Метод подстановки для решения линейных систем — это полностью алгебраический метод. Нет необходимости рисовать линии, если вас об этом не попросят.Этот метод довольно прост и всегда работает, шаги перечислены ниже. Плейлист Solving Linear Systems на YouTube
Решите систему, используя метод подстановки :
Шаг 1 : Используйте любое уравнение и найдите переменную.

В этом случае мы решили первое уравнение относительно и .

Шаг 2 : Подставьте полученную величину в другое уравнение.

Здесь мы подставили найденную величину y во второе уравнение.

Шаг 3 : Найдите оставшуюся переменную.

Шаг 4 : Выполните обратную замену, чтобы найти значение другой переменной.

Шаг 5 : Представьте свой ответ в виде упорядоченной пары ( x , y ).

Не имеет значения, выберете ли вы сначала решение для x или y . Однако убедитесь, что вы не выполняете замену в том же уравнении на шаге 2.

Помните, что мы пытаемся найти одновременные решения или точки пересечения двух линий.Далее мы увидим, что происходит, когда система является зависимой, другими словами, когда система состоит из двух одинаковых линий.

Решите систему методом подстановки :

Решите относительно и в первом уравнении. Любое истинное утверждение, включая 0 = 0, указывает на зависимую систему.
Следующая система состоит из двух параллельных линий, которые не имеют одновременного решения.

Решите систему методом подстановки :

Решите относительно x в первом уравнении.
Любое ложное утверждение указывает на несовместимость системы.

Решите системы, используя метод подстановки .
Типичная проблема со словами : Когда Джо уходил из-за стола для игры в кости, у него было 45 фишек. У него была комбинация фишек по 5 и 25 долларов, что в сумме составило 625 долларов. Сколько у него было каждой фишки?
Составьте систему двух линейных уравнений. Решите систему.
Ответ : У Джо было 25 фишек по пять долларов и 20 фишек по двадцать пять долларов.

Примеры видео на YouTube :

международных сервисных замен — Административная компания универсального обслуживания

«Глобальная» замена услуги может включать в себя продукт и / или услугу, выпуск которых прекращается, изменяется номер модели или производится замена. Кроме того, если производитель покупается или сливается с другой компанией, этот тип замены услуг должен быть подан для продуктов, произведенных исходной компанией.

Глобальная замена услуг применяется только в тех случаях, когда продукт или услуга, первоначально указанные в форме 471 Федеральной комиссии по связи, больше не доступны или больше не предоставляются поставщиком услуг. В этих случаях производитель или поставщик услуг должен уведомить USAC об изменении продукта или услуги вместе с перечислением одного или нескольких заменяющих продуктов или услуг.

Для запросов на замену услуг, инициированных производителем или поставщиком услуг, кандидатам не нужно ничего подавать в USAC для выполнения запроса.Тем не менее, изменение должно соответствовать устанавливаемой форме 470 FCC, запросу предложений (RFP), если таковые имеются, а также любым государственным и местным законам о закупках.

Когда следует подавать заявку на замену глобальной услуги

Не существует конкретных сроков для поставщиков услуг и производителей для подачи заявок на замену глобальных услуг. Однако они должны представить изменения модели как можно раньше, чтобы избежать задержек в обработке счетов. Поскольку замена услуг по инициативе поставщика услуг не ссылается на какие-либо конкретные запросы на финансирование, крайний срок предоставления услуг для запросов на финансирование, которые включают эти услуги, не продлевается автоматически.

Как подать заявку на замену глобальной услуги

Поставщики услуг должны подавать запросы на замену глобальных услуг в Центре производительности E-rate (EPC). Пошаговые инструкции см. В Руководстве пользователя EPC: Замена услуг.

При подаче заявки на замену глобальной услуги вы должны указать, что новые продукты или услуги функционально эквивалентны заменяемому продукту или услуге, и что они не увеличивают процент неприемлемых функций.USAC рекомендует поставщикам услуг включать публично опубликованное объявление о прекращении производства или изменении номера модели в письмо со своим запросом.

Замены услуг, инициированные поставщиком услуг, предназначены для размещения замен, которые USAC может подтвердить как почти идентичные. Замены, которые не могут быть обоснованы как почти идентичные, не могут быть выполнены с помощью этого подхода. Однако, если поставщик услуг знает о подобных изменениях среди многих своих клиентов, он может облегчить замену услуг среди этих клиентов, предоставив каждому клиенту одинаковые запросы на замену услуг для подписи и отправки.Подобные запросы могут быть отправлены в USAC одним запросом.

Обзор замены глобальных услуг

Поставщики услуг получат ответ на запрос замены услуги в EPC, указывающий, может ли запрос быть удовлетворен, или запрос дополнительной информации. Поставщики услуг должны предоставить копию письма одобрения USAC каждому затронутому заявителю. Кандидаты должны хранить эту копию в файле на случай аудита.

USAC будет вести список представленных заменяющих продуктов и / или услуг для обработки счетов-фактур, в которых указывается заменяющий продукт или услуга.Это избавляет многих заявителей от необходимости запрашивать одни и те же замены услуг для измененных или снятых с производства продуктов. Такая замена услуг не приведет к изменению обязательств заявителя по финансированию.

Решение

USAC обрабатывать счета с заменой конфигурации не меняет никаких договорных требований между заявителями и поставщиками услуг. Кандидаты не обязаны соглашаться с измененной конфигурацией, которая нарушает соглашение или контракт с их существующим поставщиком услуг.

Решение линейных систем заменой

Метод замещения

В этом разделе мы определим полностью алгебраический метод решения систем. Идея состоит в том, чтобы решить одно уравнение относительно одной из переменных и подставить результат в другое уравнение. После выполнения этого шага замены у нас останется одно уравнение с одной переменной, которое можно решить с помощью алгебры. Это называется методом подстановки. Средство решения линейной системы путем решения одной из переменных и подстановки результата в другое уравнение., и шаги описаны в следующем примере.

Пример 1: Решить заменой: {2x + y = 73x − 2y = −7.

Раствор:

Шаг 1: Решите для любой переменной в любом уравнении. Если вы выберете первое уравнение, вы можете выделить и за один шаг.

Шаг 2: Подставьте выражение −2x + 7 вместо переменной y в другое уравнение .

Это оставляет вам эквивалентное уравнение с одной переменной, которое можно решить, используя методы, изученные до этого момента.

Шаг 3: Найдите оставшуюся переменную. Чтобы решить относительно x , сначала распределите −2:

Шаг 4: Обратная подстановка Как только значение переменной найдено, подставьте его обратно в одно из исходных уравнений или их эквивалентных уравнений, чтобы определить соответствующее значение другой переменной.чтобы найти значение другой координаты. Подставьте x = 1 в исходные уравнения или их эквиваленты. Обычно мы используем эквивалентное уравнение, которое мы нашли при выделении переменной на шаге 1.

Решение системы: (1, 5). Обязательно представляйте решение в виде заказанной пары.

Шаг 5: Проверка. Убедитесь, что эти координаты решают оба уравнения исходной системы:

График этой линейной системы следующий:

Метод подстановки для решения систем является полностью алгебраическим методом.Таким образом, графическое отображение линий не требуется.

Ответ: (1, 5)

Пример 2: Решить заменой: {2x − y = 12x − y = 3.

Решение: В этом примере мы видим, что x имеет коэффициент 1 во втором уравнении. Это означает, что его можно изолировать за один этап следующим образом:

В первом уравнении подставьте 3 + y вместо x . Используйте круглые скобки и позаботьтесь о распространении.

Используйте x = 3 + y, чтобы найти x .

Ответ: (9, 6). Чек предоставляется читателю.

Пример 3: Решить заменой: {3x − 5y = 17x = −1.

Решение: В этом примере переменная x уже изолирована. Следовательно, мы можем подставить x = −1 в первое уравнение.

Ответ: (−1, −4). Построение графика этой конкретной системы — хорошее упражнение для сравнения метода подстановки с методом построения графиков для решения систем.

Попробуй! Решить заменой: {3x + y = 48x + 2y = 10.

Ответ: (1, 1)

Алгебраическое решение систем часто требует работы с дробями.

Пример 4: Решить заменой: {2x + 8y = 524x − 4y = −15.

Решение: Начните с решения относительно x в первом уравнении.

Затем подставляем во второе уравнение и решаем относительно y .

Обратная подстановка в уравнение, использованное на этапе замены:

Ответ: (−1/2, 3/4)

Как известно, не все линейные системы имеют только одно упорядоченное парное решение. Напомним, что некоторые системы имеют бесконечно много упорядоченных парных решений, а некоторые не имеют решений.Затем мы исследуем, что происходит при использовании метода подстановки для решения зависимой системы.

Пример 5: Решить заменой: {−5x + y = −110x − 2y = 2.

Решение: Поскольку в первом уравнении есть член с коэффициентом 1, мы решаем решить это первое.

Затем замените это выражение на y во втором уравнении.

Этот процесс привел к истинному утверждению; следовательно, уравнение является тождественным, а любое действительное число является решением.Это указывает на то, что система зависима. Одновременные решения принимают форму ( x , mx + b ) или, в данном случае, ( x , 5 x — 1), где x — любое действительное число.

Ответ: (x, 5x − 1)

Чтобы лучше понять предыдущий пример, перепишите оба уравнения в форме пересечения наклона и изобразите их на одном и том же наборе осей.

Мы видим, что оба уравнения представляют одну и ту же линию, и, следовательно, система является зависимой.Теперь рассмотрим, что происходит при решении противоречивой системы с помощью метода подстановки.

Пример 6: Решить заменой: {−7x + 3y = 314x − 6y = −16.

Решение: Решите относительно и в первом уравнении.

Подставляем во второе уравнение и решаем.

Решение приводит к ложному утверждению. Это указывает на противоречие между уравнением.Нет решения для x и, следовательно, нет решения для системы.

Ответ: Нет решения, Ø

Ложное утверждение указывает на то, что система несовместима, или в геометрических терминах, что линии параллельны и не пересекаются. Чтобы проиллюстрировать это, определите форму пересечения наклона каждой линии и изобразите их на одном и том же наборе осей.

В форме пересечения наклона легко увидеть, что две прямые имеют одинаковый наклон, но разные точки пересечения y .

Попробуй! Решить с помощью замены: {2x − 5y = 34x − 10y = 6.

Ответ: (x, 25x − 35)

Основные выводы

• Метод подстановки — это полностью алгебраический метод решения системы уравнений.
• Метод подстановки требует, чтобы мы решили одну из переменных, а затем подставили результат в другое уравнение. После выполнения шага подстановки результирующее уравнение имеет одну переменную и может быть решено с использованием методов, изученных до этого момента.
• Когда значение одной из переменных определено, вернитесь и подставьте его в одно из исходных уравнений или их эквивалентных уравнений, чтобы определить соответствующее значение другой переменной.
• Решения систем двух линейных уравнений с двумя переменными, если они существуют, представляют собой упорядоченные пары ( x , y ).
• Если процесс решения системы уравнений приводит к ложному утверждению, то система несовместима и решения нет, Ø.
• Если процесс решения системы уравнений приводит к истинному утверждению, то система является зависимой и существует бесконечно много решений, которые можно выразить в форме ( x , mx + b ).

Тематические упражнения

Часть A: Метод замещения

Решить заменой.

1. {y = 4x − 1−3x + y = 1

2.{y = 3x − 84x − y = 2

3. {x = 2y − 3x + 3y = −8

4. {x = −4y + 12x + 3y = 12

5. {y = 3x − 5x + 2y = 2

6. {y = x2x + 3y = 10

7. {y = 4x + 1−4x + y = 2

8. {y = −3x + 53x + y = 5

9. {y = 2x + 32x − y = −3

10. {y = 5x − 1x − 2y = 5

11. {y = −7x + 13x − y = 4

12. {x = 6y + 25x − 2y = 0

13. {y = −2−2x − y = −6

14.{x = −3x − 4y = −3

15. {y = −15x + 37x − 5y = 9

16. {y = 23x − 16x − 9y = 0

17. {y = 12x + 13x − 6y = 4

18. {y = −38x + 122x + 4y = 1

19. {x + y = 62x + 3y = 16

20. {x − y = 3−2x + 3y = −2

21. {2x + y = 23x − 2y = 17

22. {x − 3y = −113x + 5y = −5

23. {x + 2y = −33x − 4y = −2

24. {5x − y = 129x − y = 10

25.{x + 2y = −6−4x − 8y = 24

26. {x + 3y = −6−2x − 6y = −12

27.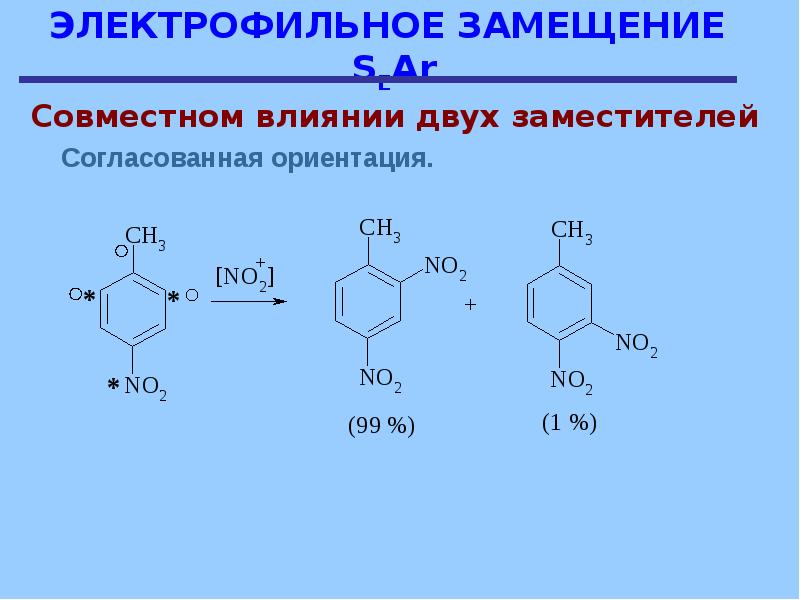 {−3x + y = −46x − 2y = −2

28. {x − 5y = −102x − 10y = −20

29. {3x − y = 94x + 3y = −1

30. {2x − y = 54x + 2y = −2

31. {−x + 4y = 02x − 5y = −6

32. {3y − x = 55x + 2y = −8

33. {2x − 5y = 14x + 10y = 2

34. {3x − 7y = −36x + 14y = 0

35. {10x − y = 3−5x + 12y = 1

36.{−13x + 16y = 2312x − 13y = −32

37. {13x + 23y = 114x − 13y = −112

38. {17x − y = 1214x + 12y = 2

39. {−35x + 25y = 1213x − 112y = −13

40. {12x = 23yx − 23y = 2

41. {−12x + 12y = 5814x + 12y = 14

42. {x − y = 0 − x + 2y = 3

43. {y = 3x2x − 3y = 0

44. {2x + 3y = 18−6x + 3y = −6

45. {−3x + 4y = 202x + 8y = 8

46. {5x − 3y = −13x + 2y = 7

47.{−3x + 7y = 22x + 7y = 1

48. {y = 3y = −3

49. {x = 5x = −2

50. {y = 4y = 4

Составьте линейную систему и решите ее с помощью метода подстановки.

51. Сумма двух чисел равна 19. Чем больше число, тем на 1 меньше, чем в три раза меньшее.

52. Сумма двух чисел равна 15. Чем больше 3, тем меньше в два раза.

53. Разница двух чисел равна 7, а их сумма равна 1.

54. Разница двух чисел равна 3, а их сумма равна −7.

55. Где на графике −5x + 3y = 30 координата x равна координате y ?

56. Где на графике 12x − 13y = 1 координата x равна координате y ?

Часть B: Темы дискуссионной доски

57. Опишите, что движет выбором переменной для решения в начале процесса решения с помощью подстановки.