НЛП — это… Что такое НЛП?
НЛП — Аббревиатура Нейролингвистическое программирование. Краткий толковый психолого психиатрический словарь. Под ред. igisheva. 2008 … Большая психологическая энциклопедия
НЛП — Аббревиатура Нейролингвистическое программирование … Универсальный дополнительный практический толковый словарь И. Мостицкого
НЛП — Нейролингвистическое программирование (НЛП) (англ. Neuro linguistic programming) (также встречается вариант «нейро лингвистическое программирование») комплекс моделей, техник и операционных принципов (контекстуально зависимых убеждений),… … Википедия
Нлп — Нейролингвистическое программирование (НЛП) (англ. Neuro linguistic programming) (также встречается вариант «нейро лингвистическое программирование») комплекс моделей, техник и операционных принципов (контекстуально зависимых убеждений),… … Википедия
НЛП — Аббревиатура Нейролингвистическое программирование … Словарь нейролингвистического программирования
НЛП — (эн эл пи)(нейро лингвистическое программирование) 1. Теория о взаимодействии человека с окружающим миром посредством внутреннего программирования. 2. Дисциплина, занимающаяся моделированием (выявлением, формализацией) и передачей… … Учебный словарь терминов рекламы и паблик рилейшенз
Теория о взаимодействии человека с окружающим миром посредством внутреннего программирования. 2. Дисциплина, занимающаяся моделированием (выявлением, формализацией) и передачей… … Учебный словарь терминов рекламы и паблик рилейшенз
НЛП — Национально либеральная партия (Ливан) национально либеральная партия нейролингвистическая психология нейролингвистическое программирование … Словарь сокращений русского языка
НЛП (значения) — НЛП: Нейролингвистическое программирование Наплавной лёгкий парк … Википедия
НЛП и наука — Одна из статей на тему Нейролингвистическое программирование (НЛП) Основные статьи НЛП · Принципы · История Новый код · НЛП и наука · Библиография Принципы и методы Раппорт · Рефрейминг · Милтон модель Репрезентативные системы · Нейрологические… … Википедия
Пресуппозиции НЛП — Эта статья о понятии нейролингвистического программирования. О термине в лингвистической семантике см. Пресуппозиция. Одна из статей на тему Нейролингвистическое программирование (НЛП) Основные статьи НЛП · Принципы · История … Википедия
О термине в лингвистической семантике см. Пресуппозиция. Одна из статей на тему Нейролингвистическое программирование (НЛП) Основные статьи НЛП · Принципы · История … Википедия
Нейролингвистическое программирование (НЛП) — презентация онлайн
1. Семинар 1_1 ПСД11-о
Выполнила:Котко Людмила Владимировна
2. Нейролингвистическое программирование (НЛП).
Система НЛП быларазработана с целью
выявления паттернов
в работе
выдающихся
специалистов в
области психологии,
и применения их
опыта, как синтеза
эффективных техник
на практике.
Ричард Бэндлер, 1950 г.р.
Джо Гриндер, 1940 г.р.
3. Специалистами, чей опыт было решено преобразовать в модели были:
Вирджиния Сатир (семейныйтерапевт),
Милтон Эриксон (эриксоноский
гипноз),
Фриц Перлз (гештальттерапевт).
4. Расшифровка термина НЛП.
«Нейро» — поведение берет начало вслушания, восприятия запаха, вкуса,
прикосновения и ощущения.
 Мы
Мывоспринимаем мир через пять своих
органов чувств
«Лингвистическое» – язык как средство
коммуникации.
«Программирование» – способы
организации идей и действий для
получения результата.
5. Карты и Фильтры
Карта – это не территория, которую онаописывает.
Мы обращаем внимание на те аспекты
мира, которые нас интересуют. и
игнорируем другие. Мир всегда богаче,
чем те идеи, которые мы имеем
относительно его.
6. Карты и Фильтры
Фильтрывосприятия
Социальный
фильтр
фильтр
НейроФизиологический
фильтр
7. Фильтры восприятия.
«Как выглядит кусок хлеба, зависит от того,голодны вы или сыты» (Арабская поговорка).
Нейрофизиологический фильтр (зрение,
слух, осязание, обоняние, вкус),
Социальный фильтр (язык,
национальность, обычаи, обряды, история
народа и государства, и др.),
Индивидуальный фильтр (мысли,
эмоции, черты характера, интересы,
привычки, симпатии, антипатии, способы
поведения, реакции, и т.
 д.).
д.).8. Поведенческие рамки
Ориентация на результат, а не напроблемы. Поиск того, к чему
стремишься, поиск решений и их
использование для продвижения к цели.
возникла эта проблема? Чья это ошибка?».
Вопрос «Как?» (понимание структуры
проблемы) вместо «Почему?» (поиск
причин и оправданий).
9. Поведенческие рамки
Обратная связь вместо неудачи.Нет неудачи – есть только результаты. Вы
можете использовать полученные
результаты для того, чтобы
скорректировать направление приложения
своих усилий. Обратная связь удерживает
цель в поле вашего зрения.
Рассматривать возможность, а не
необходимость. Сосредоточьтесь на том,
что вы можете сделать, на имеющихся
возможностях, а не на ограничивающих
вас обстоятельствах.
10. Поведенческие рамки
Позиция любопытства и удивлениявзамен притворства. Маленькие дети
помогает их любопытство.

Все мы имеем или можем создать
внутренние ресурсы, необходимые нам
для достижения наших целей. Вы с
большей вероятностью добьетесь успеха,
если будете действовать в предположении.
как будто это верно, нежели предполагая
обратное.
11. Основные мысли НЛП
Карта не соответствует местности.Опыт имеет свою структуру. Чтобы
изменить опыт, нужно поменять образец и
структуру.
Разум и тело – едины.
Все в природе взаимосвязано.
Если один человек смог сделать что-то, то
и любой другой сможет.
создать.
12. Основные мысли НЛП
Человеческое поведение имеет некоторуюцель.
Позитивное намерение в поведении
человека.
Подсознание благожелательно к нам.
Человек совершает лучший из возможных
выборов, наилучшим образом.
Иметь выбор лучше чем не иметь.
Обучение происходит через действие.
13. Основные мысли НЛП
Если вам не удается то, что вы делаете, сделайтечто-либо другое.

14. Области применения НЛП
ОтношенияВлияние на сознание масс
Переговоры,
общение
Маркетинг
Обучение
Постановка целей
психосоматика
Личностный
рост
15. Четыре стадии научения:
1. Неосознанное незнание2. Осознанное незнание
3. Осознанное знание
4. Неосознанное знание
Процесс забывания — это переход от п. 4 к
п. 2. Процесс переучивания — это переход
от п. 2 обратно к п. 4, но уже с большим
количеством выборов. Мы исследуем
различные модели научения чуть позже.
Мы способны сознательно ухватить лишь
очень маленький кусочек из того объема
информации, который мир предлагает нам,
неосознанно мы реагируем и замечаем
значительно больше, чем осознаем.
Эта идея была подчеркнута в 1956 году
американским психологом Джорджем
число семь, плюс-минус два?»
Наше подсознание — это все
жизнеобеспечивающие процессы нашего
организма, все то, чему мы уже научились,
наш прошлый опыт и все то, что мы могли бы
заметить, но не замечаем в настоящий
момент.
 Подсознание является значительно
Подсознание является значительноболее осведомленным, чем сознание.
17. Источники информации:
«Джозеф О’Коннор, Ян Мак-ДермоттПринципы NLP»
«С.Андреас и др. Миссия НЛП»
нлп, нейро лингвистическое программирование
нлп
НЛП
Расшифровка.
НЛП — эта аббревиатура стала довольно распространённой в наше время. Что же она значит? Расшифровываются эти три буквы, как нейро-лингвистическое программирование.
Откуда же взялось это название? По одной из версии Джон Гриндер и Ричард Бэндлер — основатели модели НЛП — заперлись в бревенчатой избушке, что в Калифорнийских горах и поставили себе вопрос: «Как же назвать придуманный нами метод?». Гриндер — по образованию лингвист, а Бэндлер – математик и программист. И их объединяло занятие по исследованию возможностей мышления и психофизиологии, поэтому они объединили в название этого метода три его ключевых звена:
Нейро — то есть определяет путь использования наших органов чувств.
Лингвистическое — определяет связь между языком, используемым человеком, и его жизненным опытом. То есть наши лексические модели показывают наш образ мышления и, можно сказать, наш внутренний мир.
Программирование — помогает исследовать и изменять переживания и опыт.
Зарождение.
В середине семидесятых на психотерапевтическую сцену взошли два молодых человека — Джон Гриндер и Ричард Бэндлер, которые начали обучать новому методу воздействия на человека, его поведение и ощущения. Новое программное течение, несмотря на поддержку таких звёзд, как Сатир, Эриксон и Бэйтсон, полностью игнорировалось академическими представителями. Однако вне стен университетов НЛП нашло широкий отклик в применении. Кроме того, НЛП продолжало исследования в области коммуникаций, и поэтому НЛП развивалось как коммуникативная модель.
Что даёт НЛП?
НЛП помогает скорее и результативнее достигать своих целей. Эффективные приёмы общения в духе НЛП позволяют быстрее добиваться взаимопонимания у окружающих. При этом активизируются те умственные способности, о которых вы даже не подозревали.
Наконец, благодаря нему можно научится управлять состоянием своего разума и психики.
Такой уровень самоконтроля приносит уверенность в себе и повышает самооценку. Более того, НЛП открывает более неординарный и творческий подход к решению любых проблем.
НЛП уделяет практике гораздо больше внимания, чем теории. Как правило, новички замечают, что суть теории открывается только после применения приёма.
И напоследок, НЛП – это то, благодаря чему поразительные скрытые возможности системы «разум-тело» становятся реальностью. НЛП предлагает структуру, которая поможет упрочнить ваше сознание, привить ему привычку достигать обозначенных целей.
Автор: Ольга Пашкевич
для сайта therapy. by
by
Эрик Берн — НЛП-Практика
НЛ-Программирование (1) Пять шагов программы
Мы метапрактики считаем, что термин «нейро-лингвистическое программирование» выбран в качестве титульного наименования направления деятельности совсем не случайно. Разумеется, здесь есть и аллюзии на термин “parental programming” невероятно популярного в то время Эрика Берна (и тут же «принцы» и «лягушки»), и отсылки к фундаментальному (по словам Бэндлера) труду Альфреда Коржибского (я писал об этом несколько раз). Метанимус видит в термине «программирование» буквальную метафору и указывает, что в любой нл-программе должна быть своя алгоритмическая составляющая с шагами, циклами, тестами и возвратами. Мы разделяем это его утверждение. Тем не менее, считаем, что метафора программирования как деятельности должна быть расшифрована и истолкована. Это наполнит абстрактные паруса термина полезными пресуппозициями и придаст метафоре программирования больше жизненности. Для нас же это будет полезной тренировкой в распознавании подобия (изоморфизма) и пресуппозиций. В целом такая расшифровка будет еще и утилизацией метафоры. Читать далее НЛ-Программирование (2) Необходимость расшифровки метафоры
В целом такая расшифровка будет еще и утилизацией метафоры. Читать далее НЛ-Программирование (2) Необходимость расшифровки метафоры
Периодически на меня находит желание поисследовать, откуда есть-пошло НЛП. Этакая психолого-историческая археология. Вслед за А. Ткачёвым я придерживаюсь точки зрения, что само название «нейро-лингвистическое программирование» имеет не случайное происхождение (как это последовательно утверждает Дж. Гриндер) а намеренное, и несёт в себе пресуппозиции работы самого метода, притом, это название следует понимать буквально.
На страницах журнала Метапракик мы уже разбирали термин «нейро-лингвистический». Как мы знаем, пришёл он из работы Альфреда Коржибского «Наука и психическое здоровье». С истоками термина «программирование» ясно не до конца. Во-первых, математическое образование Ричарда Бэндлера. Во-вторых, влияние известного (и гремевшего на всю Америку) тогда Эрика Берна. В книге, в которой его идеи получали максимальное развитие («What do you say after you say hello», в русском переводе «Люди, которые играют в игры»), мы встречаем термин «родительское программирование», parental programming.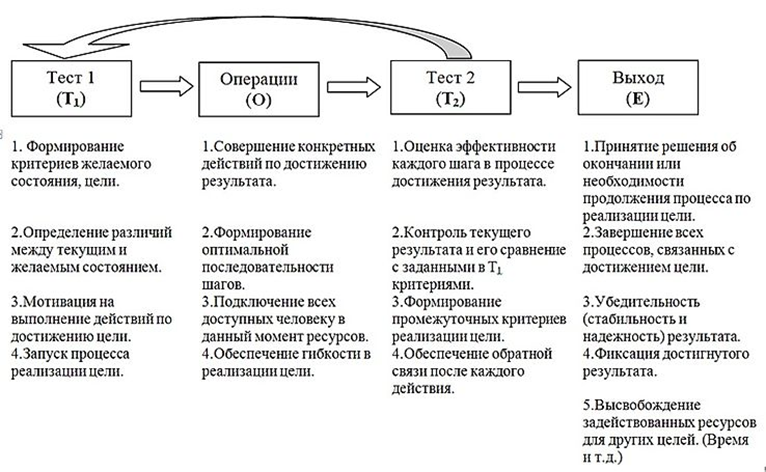 На мой взгляд, создатели НЛП успешно, вполне по-эриксониански использовали (utilized) идеи Берна и их известность, в частности, придали техническое содержание его термину «программирование». Читать далее НЛ-Программирование (1) Пять шагов программы
На мой взгляд, создатели НЛП успешно, вполне по-эриксониански использовали (utilized) идеи Берна и их известность, в частности, придали техническое содержание его термину «программирование». Читать далее НЛ-Программирование (1) Пять шагов программы
Помню давно, когда я пришел в Метапрактик, я подхватил знамёна «радикального НЛП». По аналогии со Скиннером и его «радикальным бихевиоризмом». Если есть в чем-то и нейрологическая компонента, и лингвистическая, и алгоритмическая, — значит, тут есть НЛП, и это стоит обсуждать. Нет — уж извольте. И будучи настроенным на такой лад, я все время изумлялся пиетету Метанимуса относительно трансакционного анализа. Для меня наследие Эрика Берна представлялось даже не в утрированной форме, оно представлялось мне неправильно. Меня воротило даже не от описания игр, а хотя бы даже от сценариев — как это так, думал я, чтобы пара родительских внушений определила последующую жизнь человека! Бред! А еще БиГи в своих книгах критиковали трансакционный анализ. В общем, для себя я объяснял это метанимусовской сентиментальностью — ведь он начинал свой путь в психологии именно из ТА. Читать далее Про Эрика Берна замолвлю я слово
В общем, для себя я объяснял это метанимусовской сентиментальностью — ведь он начинал свой путь в психологии именно из ТА. Читать далее Про Эрика Берна замолвлю я слово
Расшифровка… — Винницкий Центр НЛП и эриксоновского гипноза
Треугольник Карпмана: Спаситель-Жертва-Палач
(Преследователь): Вина, Праведность и другие симптомы. «Одна из прекрасных практичных моделей, созданных школой транзактного анализа, наряду со знаменитым «я ОК — ты ОК» и пр.
Знание самой модели совсем не гарантирует, что в эти игры то и дело не включаешься. Да, есть правила, которые от этих «психологических игр второго порядка» отводят, предохраняют. Но я — и не будда какой-нибудь, живущий в постоянной осознанности, и не подозрительно-начекушный параноик.
Так что время от времени ойкаю уже задним числом. Или — чаще — проскочил попытку поиграть со мной вместе, те самые правильные установки автоматически сработали. Или — ой, я в игре, — ну как мальчик!))
Страшного тут ничего нет, главное действительно быстро сообразить, что ты в шаги по треугольнику включился, и быстренько выскакивать.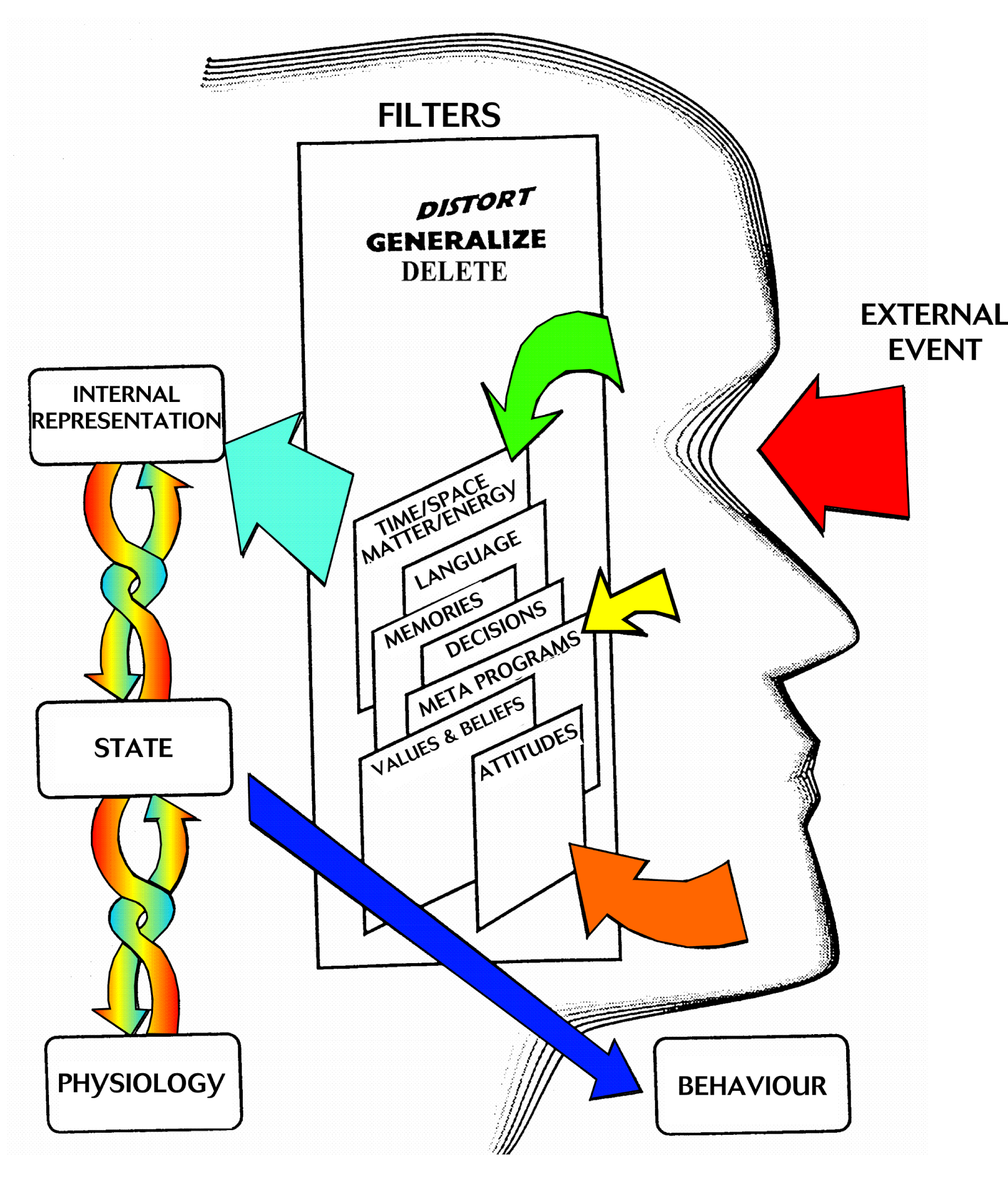
И маркер тут, когда ты внутри ситуации, — чувства.
Похоже, сильные, «чистые» (беспримесные до ненатуральности) чувства плюс их переключения («драматическая перипетия») — основные сыр и мёд этой ловушки.
Многие путают этот компот с полнотой жизни и любовью: чего-чего, а страстей тут навалом. — А, Дом-2, конечно!))
Так вот: с транзктным анализом знаком поверхностно, наверняка для себя велосипед изобрёл, ну так не в научный журнал и пишу.
Верные мгновенные сигналы, что ты вляпался, нужно «очнуться», распознать игру (расклад ролей прямо сейчас) и немедленно из неё выходить.
1. Вина! Чувство вины — полезнейший маркер, что ты — в треугольнике. Подозреваю, что, как говорят в медицине, патогномоничный (т.е. симптом, который встречается исключительно при одном заболевании и сразу позволяет его диагностировать).
2. Ощущение своей праведности, своей полноправной правоты, ликующее такое, пышущее. — Увы, туда же. Насчёт патогномоничности не знаю; но если и есть какие-то здоровые проявления, то они очень на краю. Против фашистов — о, да! — …а кого в этом сезоне считаем фашистами?..
Против фашистов — о, да! — …а кого в этом сезоне считаем фашистами?..
Ооот трижды осторожно; высочайшая вероятность на этом чувстве, что ты — там, в игре, и на следующем ходу (а ты, кстати, кто сейчас? Спаситель или Палач? шансы, так-то, 50/50, но это и не имеет значения) — и на следующем ходу роль твоя драматически сменится, и это скоро.
Почему ещё и — «Драматический треугольник».
3. Третье чувство-маркер – чувство использованности. Что ты-то со всей душой, а вышло, что тебя – использовали. Обошлись как с вещью. Попользовались – и с равнодушием, или раздражением, или прочим неблагодарным фырканьем отбросили.
4. Четвёртое чувство-маркер — стремление помочь, подставить плечо, взять на буксир… «Бойся первого движения души: оно всегда благородно». Точно, что не уникально для треугольника Карпмана. Но очень скользко, «благими намерениями дорога в ад вымощена». Признак, что именно маркер треугольника – не просто стремление помочь, а вот именно окраска «как-же-ж-иначе-ж!!»
Сам очень склонен в этой точке, Спасителем, в треугольник въезжать.
Поэтому
— три правила «неигровой» помощи.
1. Человек сам прямо просит о помощи. Не намекает, прямо просит!
2. Ты хочешь помочь ему больше, чем не хочешь. Никаких «должен». Это вопрос о том, чего ХОЧЕШЬ больше.
3. Человек для помощи себе использует хотя бы не меньше (в норме — больше!) сил, времени, энергии, чем ты для помощи ему.
Если хотя бы одно из этих трёх условий не соблюдается — ты в игре.
Можешь, — отчего бы нет, — но будь готов к интригующей и «неожиданной» смене ролей. — Я за то, что можно делать всё, если понимаешь, зачем это делаешь)
Подводя итог:
«Треугольник Карпмана» — крайне распространённый вариант манипулятивных психологических игр, в которых участники даже не отдают себе отчёт, «что их так крутит».
Есть четыре маркерных чувства, которые – ура! – позволяют «в моменте» распознать, что ты в игре.
А тогда уже быстро сориентироваться и выйти. Это вина, праведность, использованность, неодолимое стремление помочь «как-же-ж-иначе-ж».
Всё это не означает, что людям «не надо» помогать. Но есть три условия неигровой помощи. Если нарушено хотя бы одно из них – вы в игре. Это тоже можно, но хотя бы понимай, что делаешь своими руками – и принимай ответственность за последствия»
автор текста и фото
Расшифровка странного названияРасшифровка странного названияВесной 1976 года Джон и Ричард спрятались в бревенчатом домике высоко в горах неподалеку от Санта Круза, собирая вместе все прозрения и открытия, которые они сделали. К концу марафона, который длился 36 часов, они открыли бутылку красного калифорнийского вина и спросили сами себя: «Как это будет называться?» В результате получилось Нейро-Лингвистическое программирование -громоздкое словосочетание, за которым скрываются три простые идеи. Нейро – говорит об отношении к мышлению или чувственному восприятию – к процессам, протекающим в нервной системе и играющим важную роль в формировании человеческого поведения, а также к нейрологическим процессам в сфере восприятия – зрения, слуха, тактильных ощущений, вкуса и обоняния. Существенная часть НЛП связана с пониманием и использованием принципов и паттернов нервной системы. Согласно НЛП, мышление, память, творчество, создание мысленных образов и все остальные когнитивные процессы являются результатом выполнения определенных программ внутри нервной системы человека. Человеческий опыт представляет собой комбинацию или синтез информации, которую мы получаем и обрабатываем с помощью нервной системы. На практике это связано с восприятием мира через чувства: зрение, осязание, слух, обоняние и вкус. Лингвистическое указывает на то, что нервные процессы кодируются, упорядочиваются и получают значение посредством языка, коммуникативных систем и различных символических систем (грамматики, математики, музыки, изображений). С точки зрения НЛП, язык в некотором смысле является продуктом нервной системы, однако при этом стимулирует и формирует деятельность самой нервной системы. С уверенностью можно сказать, что язык представляет собой один из основных способов, которым один человек может активировать или стимулировать нервную систему других людей. Таким образом, эффективное общение и взаимодействие связаны с использованием языка для обучения, стимуляции и вербализации понятий, целей и проблем применительно к той или иной задаче или ситуации. В НЛП мы говорим о двух основных языковых системах. Во-первых, «сознание» обрабатывает информацию в терминах изображений, звуков, тактильных и вкусовых ощущений и запахов (сенсорная информация) посредством «репрезентативных систем». Сутью НЛП является установление контроля над своим собственным сознанием. Программирование относится к нашей способности организовывать эти части (изображения, звуки, тактильные и вкусовые ощущения, запахи и символы или слова) в нашем «сознании-теле», что затем позволяет нам достигать желаемых результатов. Эти части образуют программы, которые выполняет наш мозг. В основе НЛП лежит представление о том, что обучение, память и творчество являются функциями определенных нейро-лингвистических программ, которые с большей или меньшей эффективностью служат выполнению определенных задач или достижению определенных результатов. Иными словами, мы как человеческие существа осуществляем взаимодействие с окружающим миром посредством внутреннего программирования. Мы реагируем на проблемы и воспринимаем новые идеи согласно тому типу психических программ, который создали внутри себя, – а эти программы далеко не одинаковы. Некоторые программы или стратегии являются более эффективными для осуществления того или иного вида деятельности, чем другие. Программирование – указывает на тот способ, при помощи которого мы организовываем наше мышление, включая чувства и убеждения, чтобы в конечном итоге достичь поставленных целей – подобно тому, как мы используем компьютер для решения каких–либо конкретных задач при помощи соответствующего программного обеспечения. НЛП имеет дело со структурой субъективного опыта человека: как мы организуем то, что видим, слышим и ощущаем, и как мы редактируем и фильтруем с помощью органов чувств то, что получаем из внешнего мира. НЛП также исследует то, как мы описываем это в языке и как мы действуем — намеренно или ненамеренно — чтобы получить результат. Гриндер и Бандлер назвали эти модели «нейролингви-стическим программированием», так как считали, что такое название определяет сущность открытого ими явления. Мы сообщаем о своих ощущениях себе и другим двумя следующими способами: 1. Через нашу нервную систему, то есть мы с помощью разума «переводим» ощущение в психику. Примером этого может быть то, как наше тело и выражение лица отражают такую эмоцию, как восхищение, даже если мы стараемся этого не показывать. 2. Через язык, то есть с помощью особых слов и формул, описывая что-либо. Например, разница между высказываниями «Я не хочу учиться водить машину» и «Я хочу научиться летать». Вдобавок, мы учимся реагировать определенным образом на конкретные ситуации и развивать автоматические модели или программы – и на уровне нервной системы, и на уровне языка. Например, в большинстве из нас заложена программа здороваться с хорошими знакомыми, которая включает в себя то, как мы произносим приветствие, как движемся и как физически реагируем на них, и даже выражение нашего лица. Такие программы составляют большинство наших ежедневных реакций на самого себя, на других и на наше окружение, они считаются нашей личностью, нашей жизнью, просто нашим «Я». Обычно мы не останавливаемся на том, чтобы обдумать эти реакции, пока они не доставляют нам значительных проблем. Однако НЛП призывает нас осознать свои модели поведения и общения. Изучая и разъясняя модели превосходства, исследователи НЛП предложили нам структуру переосмысления своих моделей общения с самим собой и другими людьми. Исследователи НЛП приводят доказательства того, что все модели, которыми мы бессознательно пользуемся, на самом деле были усвоены нами и развиты благодаря наблюдению за другими и личному опыту. Однако, по их мнению, при желании мы можем пересмотреть свои образцы поведения и сознательно их НЛП показывает нам, как опознать свои автоматические реакции, чтобы узнать, как мы влияем на других, добиваясь определенных реакций и конкретного поведения. Мы можем выбрать, какие модели применять, чтобы активизировать собственное превосходство, а не надеяться, что оно появиться, когда будет в этом необходимость. Также мы можем заменить неподходящие модели, научиться превращать свое превосходство в автоматические программы и приобретать те модели, которые советуют исследователи НЛП. НЛП – это инструкция по применению великолепного компьютера, именуемого нашим разумом, которая дает нам возможность наиболее продуктивно им пользоваться.
|
Институт НеоКода – Новый код НЛП
личные инструменты
Вы посетили: • GROW
Модель GROW создана Джоном Уитмором как модель эффективных вопросов и является наиболее распространённым способом структурирования беседы в коучинге. Обычно вопросы задают, чтобы получить информацию. Однако в данном случае информация имеет второстепенное значение. Полученные ответы часто задают направление последующих вопросов, позволяя в то же время контролировать, следует ли клиент выбранному пути, который совпадает с целями коучинга. Как правило, это открытые вопросы, требующие описательных ответов, а не осуждения, поэтому риск впасть в самокритику или нанести ущерб самолюбию клиента отсутствует. Открытые вопросы способствуют осознанию и как следствие ответственности у клиента. Важно чтобы вопросы отвечали интересам клиента, следуя за ходом его мыслей.
Аббревиатура GROW означает ключевые точки, через которые стоит провести клиента и которые являются:
Goal — Расстановка целей, определение целей на короткий и длительный срок.
Reality — Обследование текущей ситуации на реальность.
Options — Определение списка возможностей и стратегии плана действий.
Way/Will — Намерения. «Что, когда, кем и ради чего?» будет делаться.
Ccылки по теме
Вопросы для GROW
Goal
Oписывает желаемый результат.
Это действительно цель или просто мечта?
Моя цель — из разряда «хочу» или «надо»?
Чувствую ли я воодушевление при мысли о цели?
К какой высшей цели ведет моя цель?
Конфликтует ли эта цель с чем-то еще? Другими целями, ценностями, убеждениями?
Каковы риски в случае достижения цели?
Что я потеряю, если не достигну цели?
Находится ли моя цель в зоне моей компетенции и контроля?
Конкретен ли язык, на котором описана цель?
Измерима ли моя цель?
Привязана ли к дате?
Позитивна ли?
Есть ли конкретный момент, когда я пойму, что достиг цели?
Reality
Описывает текущую ситуацию и ресурсы.
Описана ли реальность в тех же терминах, что и цель?
Включил ли я факты и цифры, где нужно?
Включил ли я допущения?
Пытался ли я уже раньше достичь цели?
Если да, то что не получалось?
Какие мнения и оценки содержатся в описании реальности?
Включил ли я описание своих чувств по поводу ситуации?
Какими ресурсами (включая навыки, контакты, информацию и т.д.) я располагаю?
Делал ли я что-либо подобное до этого?
Знаю ли я шаги, которые приведут меня к достижению цели?
На сколько процентов (шагов) выполнена цель?
Obstacles
Описывает препятствия на пути достижения цели.
Что не дает мне достичь цели?
Откуда я знаю, что это именно оно?
Что может еще помешать? (непрерывно спрашивайте себя)
Требуется ли мне изменить себя для достижения цели?
Что не дает мне измениться?
Насколько я доверяю себе в процессе?
Каковы риски в процессе достижения цели?
Это реальные риски или самооправдание?
Делаю ли я что-то прямо или косвенно для поддержания ситуации в ее текущем виде?
Есть ли у меня убеждения о том, как я должен реагировать на такого рода ситуации?
Считаю ли я, что у ситуации есть исторические причины?
Мешает ли мне кто-то? Как конкретно?
С какой целью они это делают?
Не мешает ли мне окружение в достижении цели?
Что нужно изменить в моем окружении, что поможет?
Каких ресурсов у меня нет? Способностей, навыков, информации?
Options
Описывает вариант действия.
Каков самый простой путь?
Каков может быть первый шаг?
Если бы все было возможно, что бы я сделал?
Каково идеальное решение?
Как создать ресурс, которого не хватает?
Кто может поделиться ресурсами?
На что можно обменять какие ресурсы?
Где может быть нужная информация?
Где научиться нужному навыку?
Как найти на все это время?
Был ли у меня опыт решения подобных проблем?
Что я делал в прошлом?
Что я уже делаю, что работает на достижение цели?
Существует ли проверенный способ решения таких проблем?
Знаю ли я кого-то, кто хорошо справится с такого рода препятствиями?
Есть ли какие-то группы или люди, которые готовы мне помочь?
Какие ошибки уже совершены другими до меня, которые мне совершать не обязательно?
Что на самом деле замотивирует меня?
Что принесет мне смена восприятия?
Что бы я сделал, если был более или менее настойчивым и упертым?
Как я могу изменить свою реакцию на ситуацию или человека?
По каким правилам я работаю? Откуда они взялись?
Могу ли я как-то решить эту проблему способом, который совершенно мне не свойственен?
Хватает ли мне вариантов?
Нужно ли мне устранять все препятствия?
Есть ли возможность временного решения?
Way (Will)
Описывает путь достижения результата.
Каков первый шаг, который я должен предпринять?
Каков будет второй шаг?
Знаю ли я, каким будет последний шаг?
Могу ли я мысленно пройти обратно, от последнего до первого шага?
Является ли шаг реалистичным?
Рассмотрел ли я все варианты?
Является ли мой шаг смелым?
Может ли первый шаг быть креативным?
Как мне сохранить мотивацию до конца пути?
Кто может поддержать меня на пути? (Вариант «никто» не принимается)
Куда я могу обратиться за поддержкой в первую очередь? В последнюю очередь?
На кого повлияют мои шаги? Кого я должен проинформировать?
Как я справлюсь с негативной реакцией других?
По десятибальной шкале, насколько я уверен в осуществлении плана? Что нужно сделать, чтобы быть более уверенным?
Есть ли у меня конкретные опасения по поводу моей способности осуществить план? Как я могу с ними справиться?
У всех ли шагов есть даты?
Доволен ли я в целом планом?
Как я отпраздную завершение?
Как реализовать декодер поиска луча для обработки естественного языка
Последнее обновление 3 июня 2020 г.
Задачи обработки естественного языка, такие как создание заголовков и машинный перевод, включают создание последовательностей слов.
Модели, разработанные для этих проблем, часто работают, генерируя распределения вероятностей по словарю выходных слов, и именно алгоритмы декодирования выбирают распределения вероятностей для генерации наиболее вероятных последовательностей слов.
В этом руководстве вы откроете для себя алгоритмы декодирования жадного поиска и поиска луча, которые можно использовать для решения задач генерации текста.
После прохождения этого руководства вы будете знать:
- Проблема декодирования по задачам генерации текста.
- Алгоритм декодера жадного поиска и как его реализовать на Python.
- Алгоритм декодера поиска луча и как его реализовать на Python.
Начните свой проект с моей новой книги «Глубокое обучение для обработки естественного языка», включая пошаговые руководства и файлы исходного кода Python для всех примеров.
Приступим.
- Обновление май / 2020 : Исправлена ошибка в реализации поиска луча (спасибо всем, кто указал на это, и Константину Вайссеру за его чистое исправление)
Как реализовать декодер поиска луча для обработки естественного языка
Фотография See1, Do1, Teach2, некоторые права защищены.
Декодер для генерации текста
В задачах обработки естественного языка, таких как создание заголовков, обобщение текста и машинный перевод, требуется предсказание последовательности слов.
Модели, разработанные для этих типов задач, обычно выводят распределение вероятностей по каждому слову в словаре для каждого слова в выходной последовательности. Затем процесс декодирования преобразует вероятности в окончательную последовательность слов.
Вы, вероятно, столкнетесь с этим при работе с повторяющимися нейронными сетями в задачах обработки естественного языка, где текст генерируется в качестве вывода. Последний уровень в модели нейронной сети имеет по одному нейрону для каждого слова в выходном словаре, а функция активации softmax используется для вывода вероятности того, что каждое слово в словаре будет следующим словом в последовательности.
Декодирование наиболее вероятной выходной последовательности включает поиск по всем возможным выходным последовательностям на основе их правдоподобия. Размер словарного запаса часто составляет десятки или сотни тысяч слов или даже миллионы слов. Следовательно, проблема поиска экспоненциальна по длине выходной последовательности и трудноразрешима (NP-полная) для полного поиска.
На практике методы эвристического поиска используются для возврата одной или нескольких приближенных или «достаточно хороших» декодированных выходных последовательностей для данного предсказания.
Поскольку размер поискового графа экспоненциально зависит от длины исходного предложения, мы должны использовать приближения, чтобы найти решение эффективно.
— стр. 272, Справочник по обработке естественного языка и машинному переводу, 2011 г.
Последовательности слов-кандидатов оцениваются на основе их правдоподобия. Обычно для поиска последовательностей текста-кандидатов используют жадный поиск или поиск по лучу. Мы рассмотрим оба этих алгоритма декодирования в этом посте.
Каждое индивидуальное предсказание имеет ассоциированную оценку (или вероятность), и нас интересует выходная последовательность с максимальной оценкой (или максимальной вероятностью) […] Одним из популярных приближенных методов является использование жадного предсказания, при котором на каждом этапе берется элемент с наивысшей оценкой. Хотя этот подход часто бывает эффективным, он явно неоптимален. Действительно, использование лучевого поиска в качестве приблизительного поиска часто работает намного лучше, чем жадный подход.
— страница 227, Методы нейронных сетей в обработке естественного языка, 2017.
Нужна помощь с глубоким обучением текстовых данных?
Пройдите мой бесплатный 7-дневный ускоренный курс электронной почты (с кодом).
Нажмите, чтобы зарегистрироваться, а также получите бесплатную электронную версию курса в формате PDF.
Начните БЕСПЛАТНЫЙ ускоренный курс прямо сейчас
Декодер жадного поиска
Простое приближение — использовать жадный поиск, который выбирает наиболее подходящее слово на каждом шаге выходной последовательности.
Преимущество этого подхода в том, что он очень быстр, но качество конечных выходных последовательностей может быть далеко от оптимального.
Мы можем продемонстрировать подход к декодированию с помощью жадного поиска на небольшом надуманном примере на Python.
Мы можем начать с задачи прогнозирования, которая включает последовательность из 10 слов. Каждое слово прогнозируется как распределение вероятностей по словарю из 5 слов.
# определяем последовательность из 10 слов над словарём из 5 слов данные = [[0,1, 0,2, 0,3, 0,4, 0,5], [0,5, 0,4, 0,3, 0,2, 0,1], [0,1, 0,2, 0,3, 0,4, 0,5], [0,5, 0.4, 0,3, 0,2, 0,1], [0,1, 0,2, 0,3, 0,4, 0,5], [0,5, 0,4, 0,3, 0,2, 0,1], [0,1, 0,2, 0,3, 0,4, 0,5], [0,5, 0,4, 0,3, 0,2, 0,1], [0,1, 0,2, 0,3, 0,4, 0,5], [0,5, 0,4, 0,3, 0,2, 0,1]] data = массив (данные)
# определить последовательность из 10 слов в словаре из 5 слов data = [[0,1, 0,2, 0,3, 0,4, 0,5], [0,5, 0,4, 0,3, 0,2, 0,1], [0,1 , 0,2, 0,3, 0.4, 0,5], [0,5, 0,4, 0,3, 0,2, 0,1], [0,1, 0,2, 0,3, 0,4, 0,5], [0,5, 0,4, 0,3, 0,2, 0,1], [ 0,1, 0,2, 0,3, 0,4, 0,5], [0,5, 0,4, 0,3, 0,2, 0,1], [0,1, 0,2, 0,3, 0,4, 0,5], [0,5, 0,4, 0,3, 0,2, 0,1]] данные = массив (данные) |
Предположим, что слова были закодированы в целое число, так что индекс столбца можно использовать для поиска связанного слова в словаре.Следовательно, задача декодирования становится задачей выбора последовательности целых чисел из распределений вероятностей.
Математическая функция argmax () может использоваться для выбора индекса массива, имеющего наибольшее значение. Мы можем использовать эту функцию для выбора индекса слова, который наиболее вероятен на каждом этапе последовательности. Эта функция предоставляется непосредственно в numpy.
Приведенная ниже функция greedy_decoder () реализует эту стратегию декодирования с помощью функции argmax.
# жадный декодер def greedy_decoder (данные): # индекс наибольшей вероятности для каждой строки return [argmax (s) для s в данных]
# жадный декодер def greedy_decoder (data): # индекс наибольшей вероятности для каждой строки return [argmax (s) для s в данных] |
Собрав все это вместе, полный пример, демонстрирующий жадный декодер, приведен ниже.
из массива импорта numpy из numpy import argmax # жадный декодер def greedy_decoder (данные): # индекс наибольшей вероятности для каждой строки return [argmax (s) для s в данных] # определяем последовательность из 10 слов над словарём из 5 слов данные = [[0,1, 0,2, 0,3, 0,4, 0,5], [0,5, 0,4, 0,3, 0,2, 0,1], [0,1, 0,2, 0,3, 0,4, 0,5], [0,5, 0,4, 0,3, 0,2, 0,1], [0,1, 0,2, 0,3, 0,4, 0,5], [0,5, 0,4, 0,3, 0,2, 0.1], [0,1, 0,2, 0,3, 0,4, 0,5], [0,5, 0,4, 0,3, 0,2, 0,1], [0,1, 0,2, 0,3, 0,4, 0,5], [0,5, 0,4, 0,3, 0,2, 0,1]] данные = массив (данные) # декодировать последовательность результат = greedy_decoder (данные) print (результат)
1 2 3 4 5 6 7 8 9 10 11 12 13 140002 18 19 20 21 22 23 | из массива импорта numpy из массива импорта numpy argmax # жадный декодер def greedy_decoder (data): # индекс для наибольшей вероятности каждой строки return [argmax (s) для s в данных] # определить последовательность из 10 слов в словаре из 5 слов data = [[0.1, 0,2, 0,3, 0,4, 0,5], [0,5, 0,4, 0,3, 0,2, 0,1], [0,1, 0,2, 0,3, 0,4, 0,5], [0,5, 0,4, 0,3, 0,2, 0,1], [0,1, 0,2, 0,3, 0,4, 0,5], [0,5, 0,4, 0,3, 0,2, 0,1], [0,1, 0,2, 0,3, 0,4, 0,5], [0,5, 0,4, 0,3, 0,2, 0,1], [0,1, 0,2, 0,3, 0,4, 0,5], [0,5, 0,4, 0,3, 0,2, 0,1]] данные = массив (данные) # последовательность декодирования результат = greedy_decoder (данные) печать (результат) |
При выполнении примера выводится последовательность целых чисел, которая затем может быть снова отображена на слова в словаре.
[4, 0, 4, 0, 4, 0, 4, 0, 4, 0]
[4, 0, 4, 0, 4, 0, 4, 0, 4, 0] |
Декодер поиска луча
Еще одна популярная эвристика — поиск по лучу, который расширяет жадный поиск и возвращает список наиболее вероятных выходных последовательностей.
Вместо того, чтобы жадно выбирать наиболее вероятный следующий шаг при построении последовательности, поиск луча расширяет все возможные следующие шаги и сохраняет k наиболее вероятным, где k является параметром, задаваемым пользователем и управляет количеством лучей или параллельный поиск по последовательности вероятностей.
Алгоритм поиска локального луча отслеживает k состояний, а не только одно. Он начинается с k случайно сгенерированных состояний. На каждом шаге генерируются все преемники всех k состояний. Если какая-либо цель является целью, алгоритм останавливается. В противном случае он выбирает k лучших последователей из полного списка и повторяет.
— страницы 125-126, Искусственный интеллект: современный подход (3-е издание), 2009 г.
Нам не нужно начинать со случайных состояний; вместо этого мы начинаем с k наиболее вероятных слов в качестве первого шага в последовательности.
Общие значения ширины луча: 1 для жадного поиска и значения 5 или 10 для общих проблем эталонных тестов при машинном переводе. Большая ширина луча приводит к лучшей производительности модели, поскольку несколько последовательностей-кандидатов увеличивают вероятность лучшего совпадения целевой последовательности. Эта повышенная производительность приводит к снижению скорости декодирования.
В NMT новые предложения переводятся простым декодером поиска луча, который находит перевод, который приблизительно максимизирует условную вероятность обученной модели NMT.Стратегия поиска луча генерирует перевод слово за словом слева направо, сохраняя при этом фиксированное количество (луч) активных кандидатов на каждом временном шаге. Увеличивая размер луча, можно повысить эффективность трансляции за счет значительного снижения скорости декодера.
— Стратегии поиска луча для нейронного машинного перевода, 2017.
Процесс поиска может останавливаться для каждого кандидата отдельно либо по достижении максимальной длины, по достижению маркера конца последовательности, либо по достижению пороговой вероятности.
Приведем конкретный пример.
Мы можем определить функцию для выполнения поиска луча для заданной последовательности вероятностей и параметра ширины луча k . На каждом шаге каждая последовательность-кандидат дополняется всеми возможными следующими шагами. Каждый возможный шаг оценивается путем умножения вероятностей. Выбираются последовательности k с наиболее вероятными вероятностями, а все другие кандидаты удаляются. Затем процесс повторяется до конца последовательности.
Вероятности — это маленькие числа, и их умножение дает очень маленькие числа. Чтобы избежать потери значимости чисел с плавающей запятой, натуральный логарифм вероятностей суммируется, что позволяет сохранять числа больше и удобнее. Кроме того, поиск часто выполняется путем минимизации оценки. Эта последняя настройка означает, что мы можем отсортировать все последовательности-кандидаты в порядке возрастания по их баллам и выбрать первые k в качестве наиболее вероятных последовательностей-кандидатов.
Функция beam_search_decoder () ниже реализует декодер поиска луча.
# поиск луча def beam_search_decoder (данные, k): последовательности = [[список (), 0,0]] # пройдемся по каждому шагу последовательно для строки в данных: all_candidates = список () # развернуть каждого текущего кандидата для i в диапазоне (len (последовательности)): seq, score = последовательностей [i] для j в диапазоне (len (строка)): кандидат = [seq + [j], оценка — журнал (строка [j])] all_candidates.добавить (кандидат) # упорядочить всех кандидатов по баллам заказанный = отсортированный (all_candidates, key = lambda tup: tup [1]) # выберите k лучших последовательности = заказанные [: k] возвращаемые последовательности
1 2 3 4 5 6 7 8 9 10 11 12 13 140002 14 | # поиск лучей def beam_search_decoder (data, k): последовательностей = [[list (), 0.0]] # пройти каждый шаг в последовательности для строки в данных: all_candidates = list () # развернуть каждого текущего кандидата для i в диапазоне (len (последовательности)): seq, оценка = последовательности [i] для j в диапазоне (len (строка)): кандидат = [seq + [j], оценка — журнал (строка [j])] all_candidates.append (кандидат) # упорядочить всех кандидатов по количеству баллов упорядочено = отсортировано (all_candidates, key = lambda tup: tup [1]) # выбрать k лучших последовательностей = упорядочено [: k] возвращаемых последовательностей |
Мы можем связать это вместе с образцами данных из предыдущего раздела и на этот раз вернуть 3 наиболее вероятные последовательности.
из журнала импорта математики из массива импорта numpy из numpy import argmax # поиск луча def beam_search_decoder (данные, k): последовательности = [[список (), 0,0]] # пройдемся по каждому шагу последовательно для строки в данных: all_candidates = список () # развернуть каждого текущего кандидата для i в диапазоне (len (последовательности)): seq, score = последовательностей [i] для j в диапазоне (len (строка)): кандидат = [seq + [j], оценка — журнал (строка [j])] all_candidates.добавить (кандидат) # упорядочить всех кандидатов по баллам заказанный = отсортированный (all_candidates, key = lambda tup: tup [1]) # выберите k лучших последовательности = заказанные [: k] возвращаемые последовательности # определяем последовательность из 10 слов над словарём из 5 слов данные = [[0,1, 0,2, 0,3, 0,4, 0,5], [0,5, 0,4, 0,3, 0,2, 0,1], [0,1, 0,2, 0,3, 0,4, 0,5], [0,5, 0,4, 0,3, 0,2, 0,1], [0,1, 0,2, 0,3, 0,4, 0,5], [0,5, 0,4, 0,3, 0,2, 0,1], [0,1, 0,2, 0,3, 0,4, 0.5], [0,5, 0,4, 0,3, 0,2, 0,1], [0,1, 0,2, 0,3, 0,4, 0,5], [0,5, 0,4, 0,3, 0,2, 0,1]] данные = массив (данные) # декодировать последовательность результат = beam_search_decoder (данные, 3) # результат печати для seq в результате: печать (seq)
1 2 3 4 5 6 7 8 9 10 11 12 13 140002 18 19 20 21 22 23 24 25 26 27 28 29 30 000 000 34 35 36 37 38 39 | из журнала импорта math из массива импорта numpy из массива импорта numpy argmax # beam search def beam_search_decoder (data, k): последовательностей = [[list (), 0.0]] # пройти каждый шаг в последовательности для строки в данных: all_candidates = list () # развернуть каждого текущего кандидата для i в диапазоне (len (последовательности)): seq, оценка = последовательности [i] для j в диапазоне (len (строка)): кандидат = [seq + [j], оценка — журнал (строка [j])] all_candidates.append (кандидат) # упорядочить всех кандидатов по количеству баллов упорядочено = отсортировано (all_candidates, key = lambda tup: tup [1]) # выбрать k лучших последовательностей = упорядочено [: k] возвращаемых последовательностей # определить последовательность из 10 слов в словаре из 5 слов data = [[0.1, 0,2, 0,3, 0,4, 0,5], [0,5, 0,4, 0,3, 0,2, 0,1], [0,1, 0,2, 0,3, 0,4, 0,5], [0,5, 0,4, 0,3, 0,2, 0,1], [0,1, 0,2, 0,3, 0,4, 0,5], [0,5, 0,4, 0,3, 0,2, 0,1], [0,1, 0,2, 0,3, 0,4, 0,5], [0,5, 0,4, 0,3, 0,2, 0,1], [0,1, 0,2, 0,3, 0,4, 0,5], [0,5, 0,4, 0,3, 0,2, 0,1]] данные = массив (данные) # последовательность декодирования результат = beam_search_decoder (data, 3) # print result для seq in result: print (seq) |
При выполнении примера печатаются как целочисленные последовательности, так и их логическая вероятность.
Поэкспериментируйте с разными значениями k.
[[4, 0, 4, 0, 4, 0, 4, 0, 4, 0], 6.931471805599453]
[[4, 0, 4, 0, 4, 0, 4, 0, 4, 1], 7.1546153563]
[[4, 0, 4, 0, 4, 0, 4, 0, 3, 0], 7.1546153563]
[[4, 0, 4, 0, 4, 0, 4, 0, 4, 0], 6.931471805599453] [[4, 0, 4, 0, 4, 0, 4, 0, 4, 1 ], 7.154615356 [[4, 0, 4, 0, 4, 0, 4, 0, 3, 0], 7.154615356 |
Дополнительная литература
Этот раздел предоставляет дополнительные ресурсы по теме, если вы хотите углубиться.
Сводка
В этом руководстве вы открыли для себя алгоритмы декодирования жадного поиска и поиска по лучу, которые можно использовать для решения задач генерации текста.
В частности, вы выучили:
- Проблема декодирования по задачам генерации текста.
- Алгоритм декодера жадного поиска и как его реализовать на Python.
- Алгоритм декодера поиска луча и как его реализовать на Python.
Есть вопросы?
Задайте свои вопросы в комментариях ниже, и я постараюсь ответить.
Разрабатывайте модели глубокого обучения для текстовых данных уже сегодня!
Разработка собственных текстовых моделей за считанные минуты
... всего несколькими строками кода Python
Узнайте, как это сделать, в моей новой электронной книге:
Deep Learning for Natural Language Processing
Он предоставляет самоучителей по таким темам, как:
Пакет слов, встраивание слов, языковые модели, создание титров, перевод текста и многое другое ...
Наконец-то привнесите глубокое обучение в свои проекты обработки естественного языка
Пропустить академики.Только результаты.
Посмотрите, что внутриРуководство по модели кодировщика-декодера и механизму внимания | Эдуардо Муньос
Как мы упоминали ранее, мы заинтересованы в групповом обучении сети; поэтому мы создаем функцию, которая выполняет обучение пакета данных:
- Вызвать кодировщик для последовательности пакетного ввода - на выходе будет закодированный вектор
- Установить начальные состояния декодера на закодированный вектор
- Вызов декодер, принимая в качестве входных данных целевую последовательность со смещением вправо.Выходные данные - логиты (функция softmax применяется в функции потерь).
- Вычислить потерю и точность пакетных данных
- Обновить обучаемые параметры кодера и декодера
- Обновить оптимизатор
Как вы можете заметить, наша функция поезда принимает три последовательности:
- Входная последовательность: массив целых чисел формы:
[batch_size, max_seq_len, embedding dim]. Это входная последовательность для кодировщика. - Целевая последовательность: Массив целых чисел формы:
[batch_size, max_seq_len, embedding dim].Это цель нашей модели, результат, который нам нужен для нашей модели. - Целевая входная последовательность: Массив целых чисел формы:
[batch_size, max_seq_len, embedding dim]. Это входная последовательность для декодера, потому что мы используем учитель, заставляющий .
Принуждение учителя
Принуждение учителя - это метод обучения, критически важный для разработки моделей глубокого обучения в НЛП. «Это способ быстрого и эффективного обучения повторяющихся моделей нейронных сетей, которые используют в качестве входных данных достоверную информацию из предыдущего временного шага.», [8]« Что учитель заставляет использовать рекуррентные нейронные сети? » Джейсон Браунли, доктор философии
В рекуррентной сети обычно входом в RNN на временном шаге t является выход RNN на предыдущем временном шаге, t-1. Но с помощью принуждения учителя мы можем использовать фактический результат для улучшения обучающих возможностей модели.
«Принуждение учителя работает с использованием фактических или ожидаемых выходных данных из набора обучающих данных на текущем временном шаге y (t) в качестве входных данных на следующем временном шаге X (t + 1), а не выходных данных, генерируемых сетью.
- «Глубокое обучение» Иэна Гудфеллоу
Итак, в нашем примере целевой вывод на временном шаге t является входом декодера на временном шаге t + 1. Наша входная последовательность для декодера будет ожидаемой целевой последовательностью, сдвинутой на одну позицию вправо. Для этого мы вставляем начальный токен последовательности в первую позицию, чтобы токен в позиции 1 переместился в позицию 2, токен с 2 по 3 и так далее. Чтобы уравнять длины последовательностей и разграничить их конец, в целевой последовательности мы поместим маркер конца последовательности в последнюю позицию.
Когда результат нашей модели не отличается от того, что было видно на модели во время обучения, принуждение учителя очень эффективно. Но если нам нужна более креативная модель, в которой при заданной входной последовательности может быть несколько возможных выходов, мы должны избегать этого метода или применять его случайным образом (только в некоторых случайных временных шагах).
Теперь мы можем закодировать основную функцию поезда:
Мы почти готовы - наш последний шаг включает вызов основной функции поезда, и мы создаем объект контрольной точки для сохранения нашей модели.Поскольку тренировочный процесс требует длительного времени, мы будем сохранять его каждые две эпохи. Позже мы сможем восстановить его и использовать для прогнозов.
Мы обучаем нашу модель кодировщика-декодера в течение ограниченного периода времени (примерно один час), используя 40 000 пар предложений и RNN из 512 единиц. Мы достигаем хороших результатов:
Делаем прогнозы
На этапе прогнозирования входными данными является последовательность длины один, токен sos . Затем мы повторно вызываем кодировщик и декодер, пока не получим токен eos или не достигнем максимальной заданной длины.
Вот несколько примеров полученных нами прогнозов:
[«мы не пойдем», «почему тебе грустно?»]
[«нет вамос.',' ¿por que estas triste? ']
Трансформаторные модели кодировщика-декодера
! Pip install трансформаторы == 4.2.1
! pip install фраза == 0.1.95
Модель кодера-декодера на основе трансформатора была представлена Васвани. и другие. в знаменитом Attention - это все, что вам нужно бумаги и сегодня это де-факто стандартная архитектура кодера-декодера при обработке естественного языка (НЛП).
В последнее время было проведено много исследований по разным предварительному обучению объективы для моделей кодеров-декодеров на базе трансформаторов, , например Т5, Барт, Пегас, ProphetNet, Мардж, и т. Д. ..., но модель архитектуры остался в основном прежним.
Цель сообщения в блоге - дать подробное объяснение как модели архитектуры кодера-декодера на основе трансформатора от последовательности к последовательности проблемы.Сфокусируемся на математической модели определяется архитектурой и тем, как модель может использоваться для вывода. Попутно мы дадим некоторую справочную информацию о последовательности в последовательность. модели в NLP и разбить кодировщик-декодер на базе трансформатора архитектура в его кодировщика и декодера частей. Мы предоставляем много иллюстрации и установить связь между теорией модели кодеров-декодеров на базе трансформаторов и их практическое применение в 🤗Трансформаторы для вывода.Обратите внимание, что это сообщение в блоге не объясняет , а не как такие модели можно обучить - это тема будущего блога Почта.
Модели кодировщиков-декодеров на базе трансформаторов являются результатом многолетней Исследование представлений , изучение архитектур моделей и . Этот Блокнот содержит краткое изложение истории нейронных кодировщики-декодеры модели. Для получения дополнительной информации читателю рекомендуется прочитать этот замечательный блог опубликовать Себастион Рудер. Кроме того, базовое понимание рекомендуется архитектура с самовниманием .Следующее сообщение в блоге автора Джей Аламмар служит хорошим напоминанием об оригинальной модели Transformer. здесь.
На момент написания этого блокнота «Трансформеры включают кодировщики-декодеры моделей T5 , Bart , MarianMT и Pegasus , которые кратко описаны в документации по модели резюме.
Ноутбук разделен на четыре части:
- Предпосылки - Краткая история моделей нейронных кодировщиков-декодеров дается с акцентом на модели на основе RNN.
- Кодер-декодер - Модель кодера-декодера на основе трансформатора представлена и объясняется, как модель используется для вывод.
- Энкодер - Часть модели энкодера объяснена в деталь.
- Декодер - Декодерная часть модели объяснена в деталь.
Каждая часть основана на предыдущей части, но также может быть прочитана на ее собственный.
ФонЗадачи генерации естественного языка (NLG), подполе NLP, являются лучшими выражаются как задачи от последовательности к последовательности.Такие задачи можно определить как поиск модели, которая отображает последовательность входных слов в последовательность целевые слова. Некоторые классические примеры - это суммирование и перевод . Далее мы предполагаем, что каждое слово закодировано в векторное представление. входные слова nnn могут быть представлены как последовательность входных векторов nnn:
X1: n = {x1,…, xn}. \ Mathbf {X} _ {1: n} = \ {\ mathbf {x} _1, \ ldots, \ mathbf {x} _n \}. X1: n = {x1,…, xn}.
Следовательно, проблемы от последовательности к последовательности могут быть решены путем нахождения отображение fff из входной последовательности nnn векторов X1: n \ mathbf {X} _ {1: n} X1: n в последовательность целевых векторов mmm Y1: m \ mathbf {Y} _ {1: m} Y1: m, тогда как число векторов-мишеней ммм априори неизвестен и зависит от входных данных последовательность:
f: X1: n → Y1: m.22 для решения задач от последовательности к последовательности следовательно, означает, что необходимо знать количество целевых векторов mmm apriori и должен быть независимым от ввода X1: n \ mathbf {X} _ {1: n} X1: n. Это неоптимально, потому что для задач в NLG количество целевых слов обычно зависит от ввода X1: n \ mathbf {X} _ {1: n} X1: n и не только на входной длине nnn. Например. , статья 1000 слов можно суммировать как до 200 слов, так и до 100 слов в зависимости от его содержание.
В 2014 г. Cho et al.33. После обработки последнего входного вектора xn \ mathbf {x} _nxn, Скрытое состояние кодировщика определяет входную кодировку c \ mathbf {c} c. Таким образом, кодировщик определяет отображение:
fθenc: X1: n → c. f _ {\ theta_ {enc}}: \ mathbf {X} _ {1: n} \ to \ mathbf {c}. fθenc: X1: n → c.
Затем скрытое состояние декодера инициализируется входной кодировкой. и во время логического вывода декодер RNN используется для авторегрессивного генерировать целевую последовательность. Поясним.
Математически декодер определяет распределение вероятностей целевая последовательность Y1: m \ mathbf {Y} _ {1: m} Y1: m с учетом скрытого состояния c \ mathbf {c} c:
pθdec (Y1: m∣c).{m} p _ {\ theta _ {\ text {dec}}} (\ mathbf {y} _i | \ mathbf {Y} _ {0: i-1}, \ mathbf {c}). pθdec (Y1: m ∣c) = i = 1∏m pθdec (yi ∣Y0: i − 1, c).
Таким образом, если архитектура может моделировать условное распределение следующий целевой вектор, учитывая все предыдущие целевые векторы:
pθdec (yi∣Y0: i − 1, c), ∀i∈ {1,…, m}, p _ {\ theta _ {\ text {dec}}} (\ mathbf {y} _i | \ mathbf {Y} _ {0: i-1}, \ mathbf {c}), \ forall i \ in \ {1, \ ldots, m \}, pθdec (yi ∣Y0: i − 1, c), ∀ i∈ {1,…, m},
, то он может моделировать распределение любой последовательности целевого вектора, заданной скрытое состояние c \ mathbf {c} c путем простого умножения всех условных вероятности.
Так как же модель архитектуры декодера на основе RNN pθdec (yi∣Y0: i − 1, c) p _ {\ theta _ {\ text {dec}}} (\ mathbf {y} _i | \ mathbf {Y} _ { 0: i-1}, \ mathbf {c}) pθdec (yi ∣Y0: i − 1, c)?
С точки зрения вычислений, модель последовательно отображает предыдущий внутренний скрытое состояние ci − 1 \ mathbf {c} _ {i-1} ci − 1 и предыдущий целевой вектор yi \ mathbf {y} _iyi до текущего внутреннего скрытого состояния ci \ mathbf {c} _ici и a вектор logit li \ mathbf {l} _ili (показано темно-красным цветом ниже):
fθdec (yi − 1, ci − 1) → li, ci.f _ {\ theta _ {\ text {dec}}} (\ mathbf {y} _ {i-1}, \ mathbf {c} _ {i-1}) \ to \ mathbf {l} _i, \ mathbf {c } _i.fθdec (yi − 1, ci − 1) → li, ci. c0 \ mathbf {c} _0c0 таким образом определяется как c \ mathbf {c} c, являющийся выходом скрытое состояние кодировщика на основе RNN. Впоследствии softmax используется для преобразования вектора логита li \ mathbf {l} _ili в условное распределение вероятностей следующего целевого вектора:
p (yi∣li) = Softmax (li), где li = fθdec (yi − 1, cprev). p (\ mathbf {y} _i | \ mathbf {l} _i) = \ textbf {Softmax} (\ mathbf {l} _i), \ text {with} \ mathbf {l} _i = f _ {\ theta _ {\ text {dec}}} (\ mathbf {y} _ {i-1}, \ mathbf {c} _ {\ text {prev}}).44. Из приведенного выше уравнения мы можно видеть, что распределение текущего целевого вектора yi \ mathbf {y} _iyi напрямую обусловлено предыдущим целевым вектором yi − 1 \ mathbf {y} _ {i-1} yi − 1 и предыдущим скрытым состоянием ci −1 \ mathbf {c} _ {i-1} ci − 1. Поскольку предыдущее скрытое состояние ci − 1 \ mathbf {c} _ {i-1} ci − 1 зависит от всех предыдущие целевые векторы y0,…, yi − 2 \ mathbf {y} _0, \ ldots, \ mathbf {y} _ {i-2} y0,…, yi − 2, он может быть заявлено, что декодер на основе RNN неявно ( например, косвенно ) моделирует условное распределение pθdec (yi∣Y0: i − 1, c) p _ {\ theta _ {\ text {dec}}} (\ mathbf {y} _i | \ mathbf {Y} _ {0: i-1}, \ mathbf {c}) pθdec (yi ∣Y0: i − 1, c).55, которые эффективно выбирают целевой вектор с высокой вероятностью последовательности из pθdec (Y1: m∣c) p _ {\ theta_ {dec}} (\ mathbf {Y} _ {1: m} | \ mathbf {c}) pθdec (Y1: m ∣c).
При таком методе декодирования во время вывода следующий входной вектор yi \ mathbf {y} _iyi может быть выбран из pθdec (yi∣Y0: i − 1, c) p _ {\ theta _ {\ text {dec}} } (\ mathbf {y} _i | \ mathbf {Y} _ {0: i-1}, \ mathbf {c}) pθdec (yi ∣Y0: i − 1, c) и, следовательно, добавляется к входной последовательности, так что декодер Затем RNN моделирует pθdec (yi + 1∣Y0: i, c) p _ {\ theta _ {\ text {dec}}} (\ mathbf {y} _ {i + 1} | \ mathbf {Y} _ {0: i }, \ mathbf {c}) pθdec (yi + 1 ∣Y0: i, c) для выборки следующего входного вектора yi + 1 \ mathbf {y} _ {i + 1} yi + 1 и т. д. в авторегрессивный мод.
Важной особенностью моделей кодеров-декодеров на основе RNN является определение специальных векторов , таких как вектор EOS \ text {EOS} EOS и BOS \ text {BOS} BOS. Вектор EOS \ text {EOS} EOS часто представляет собой окончательный входной вектор xn \ mathbf {x} _nxn, чтобы "указать" кодировщику, что вход последовательность закончилась, а также определяет конец целевой последовательности. В качестве как только EOS \ text {EOS} EOS выбирается из вектора логита, генерация завершено. Вектор BOS \ text {BOS} BOS представляет входной вектор y0 \ mathbf {y} _0y0, подаваемый в декодер RNN на самом первом этапе декодирования.Для вывода первого логита l1 \ mathbf {l} _1l1 требуется ввод, и поскольку на первом шаге не было создано никаких входных данных. специальный BOS \ text {BOS} BOS входной вектор поступает на декодер RNN. Хорошо - довольно сложно! Давайте проиллюстрируйте и рассмотрите пример.
Развернутый кодировщик RNN окрашен в зеленый цвет, а развернутый RNN декодер окрашен в красный цвет.
Английское предложение «Я хочу купить машину», представленное как x1 = I \ mathbf {x} _1 = \ text {I} x1 = I, x2 = want \ mathbf {x} _2 = \ text {want} x2 = хочу, x3 = to \ mathbf {x} _3 = \ text {to} x3 = to, x4 = buy \ mathbf {x} _4 = \ text {buy} x4 = buy, x5 = a \ mathbf {x} _5 = \ text {a} x5 = a, x6 = car \ mathbf {x} _6 = \ text {car} x6 = car и x7 = EOS \ mathbf {x} _7 = \ text {EOS} x7 = EOS переводится на немецкий: "Ich will ein Auto kaufen "определяется как y0 = BOS \ mathbf {y} _0 = \ text {BOS} y0 = BOS, y1 = Ich \ mathbf {y} _1 = \ text {Ich} y1 = Ich, y2 = will \ mathbf {y} _2 = \ text {will} y2 = will, y3 = ein \ mathbf {y} _3 = \ text {ein} y3 = ein, y4 = Auto, y5 = kaufen \ mathbf {y} _4 = \ text {Auto}, \ mathbf {y} _5 = \ text {kaufen} y4 = Auto, y5 = kaufen и y6 = EOS \ mathbf {y} _6 = \ text {EOS} y6 = EOS. 66.На рисунке выше горизонтальная стрелка, соединяющая развернутый кодировщик RNN представляет собой последовательные обновления скрытых штат. Окончательное скрытое состояние кодировщика RNN, представленное c \ mathbf {c} c, затем полностью определяет кодировку входных данных. последовательность и используется как начальное скрытое состояние декодера RNN. Это можно увидеть как преобразование декодера RNN на закодированный вход.
Для генерации первого целевого вектора в декодер загружается BOS \ text {BOS} BOS вектор, показанный как y0 \ mathbf {y} _0y0 на рисунке выше.Цель вектор RNN затем дополнительно преобразуется в вектор логита l1 \ mathbf {l} _1l1 с помощью уровня прямой связи LM Head для определения условное распределение первого целевого вектора, как объяснено выше:
pθdec (y∣BOS, c). p _ {\ theta_ {dec}} (\ mathbf {y} | \ text {BOS}, \ mathbf {c}). pθdec (y∣BOS, c).
Выбирается слово Ich \ text {Ich} Ich (показано серой стрелкой, соединяющей l1 \ mathbf {l} _1l1 и y1 \ mathbf {y} _1y1) и, следовательно, вторая цель вектор может быть выбран:
будет ∼pθdec (y∣BOS, Ich, c).\ text {will} \ sim p _ {\ theta_ {dec}} (\ mathbf {y} | \ text {BOS}, \ text {Ich}, \ mathbf {c}). will∼pθdec (y∣BOS, Ich, c).
И так далее, пока на шаге i = 6i = 6i = 6, вектор EOS \ text {EOS} EOS не будет выбран из l6 \ mathbf {l} _6l6, и декодирование не будет завершено. Результирующая цель последовательность составляет Y1: 6 = {y1,…, y6} \ mathbf {Y} _ {1: 6} = \ {\ mathbf {y} _1, \ ldots, \ mathbf {y} _6 \} Y1: 6 = {y1,…, y6}, что является «Ich will ein Auto kaufen» в нашем примере выше.
Подводя итог, модель кодера-декодера на основе RNN, представленная fθencf _ {\ theta _ {\ text {enc}}} fθenc и pθdec p _ {\ theta _ {\ text {dec}}} pθdec, определяет распределение p (Y1: m∣X1: n) p (\ mathbf {Y} _ {1: m} | \ mathbf {X} _ {1: n}) p (Y1: m ∣X1: n) к факторизация:
pθenc, θdec (Y1: m∣X1: n) = ∏i = 1mpθenc, θdec (yi∣Y0: i − 1, X1: n) = ∏i = 1mpθdec (yi∣Y0: i − 1, c), с c = fθenc (X).{m} p _ {\ theta _ {\ text {dec}}} (\ mathbf {y} _i | \ mathbf {Y} _ {0: i-1}, \ mathbf {c}), \ text {with} \ mathbf {c} = f _ {\ theta_ {enc}} (X). pθenc, θdec (Y1: m ∣X1: n) = i = 1∏m pθenc, θdec (yi ∣Y0: i − 1, X1: n) = i = 1 ∏m pθdec (yi ∣Y0: i − 1, c), где c = fθenc (X).
Во время вывода эффективные методы декодирования могут авторегрессивно сгенерировать целевую последовательность Y1: m \ mathbf {Y} _ {1: m} Y1: m.
Модель кодера-декодера на основе RNN взяла штурмом сообщество NLG. В В 2016 г. компания Google объявила о полной замене разработанной услуги перевода с помощью единой модели кодировщика-декодера на основе RNN (см. здесь).44 Нейронная сеть может определять распределение вероятностей по всем слова, , т.е. p (y∣c, Y0: i − 1) p (\ mathbf {y} | \ mathbf {c}, \ mathbf {Y} _ {0: i-1}) p (y∣c , Y0: i − 1) как следует. Сначала сеть определяет отображение входов c, Y0: i − 1 \ mathbf {c}, \ mathbf {Y} _ {0: i-1} c, Y0: i − 1 во встроенное векторное представление y ′ \ Mathbf {y '} y ′, что соответствует целевому вектору RNN. Встроенный векторное представление y ′ \ mathbf {y '} y ′ затем передается на "язык модель головы ", что означает, что он умножается на слова. матрица внедрения , i.66 Sutskever et al. (2014) меняет порядок ввода так, чтобы в приведенном выше примере ввод векторы будут соответствовать x1 = car \ mathbf {x} _1 = \ text {car} x1 = car, x2 = a \ mathbf {x} _2 = \ text {a} x2 = a, x3 = buy \ mathbf { x} _3 = \ text {buy} x3 = buy, x4 = to \ mathbf {x} _4 = \ text {to} x4 = to, x5 = want \ mathbf {x} _5 = \ text {want} x5 = Хочу, x6 = I \ mathbf {x} _6 = \ text {I} x6 = I и x7 = EOS \ mathbf {x} _7 = \ text {EOS} x7 = EOS. В мотивация состоит в том, чтобы обеспечить более короткую связь между соответствующими пары слов, такие как x6 = I \ mathbf {x} _6 = \ text {I} x6 = I и y1 = Ich \ mathbf {y} _1 = \ text {Ich} y1 = Ich.Исследовательская группа подчеркивает, что обращение входной последовательности было ключевой причиной того, что их модель улучшена производительность машинного перевода.
Кодер-декодерВ 2017 г. Vaswani et al. представил трансформатор Transformer и тем самым дал рождение модели на базе трансформатора кодировщика-декодера .
Аналогичен моделям кодировщика-декодера на базе RNN, трансформаторный Модели кодировщика-декодера состоят из кодировщика и декодера, которые обе стопки из блоков остаточного внимания .Ключевое новшество трансформаторные модели кодировщика-декодера заключается в том, что такое остаточное внимание блоки могут обрабатывать входную последовательность X1: n \ mathbf {X} _ {1: n} X1: n переменной длина nnn без отображения повторяющейся структуры. Не полагаясь на рекуррентная структура позволяет преобразовывать кодировщики-декодеры высокая степень распараллеливания, что делает модель на порядки больше вычислительно эффективен, чем модели кодировщика-декодера на основе RNN на современное оборудование.
Напоминаем, что для решения задачи от последовательности к последовательности нам необходимо найти отображение входной последовательности X1: n \ mathbf {X} _ {1: n} X1: n на выход последовательность Y1: m \ mathbf {Y} _ {1: m} Y1: m переменной длины mmm.Посмотрим как модели кодеров-декодеров на основе трансформаторов используются для поиска такого отображение.
Подобно моделям кодировщика-декодера на основе RNN, трансформатор на основе модели кодировщика-декодера определяют условное распределение целевых векторы Y1: n \ mathbf {Y} _ {1: n} Y1: n с заданной входной последовательностью X1: n \ mathbf {X} _ {1: n} X1: n:
pθenc, θdec (Y1: m∣X1: n). p _ {\ theta _ {\ text {enc}}, \ theta _ {\ text {dec}}} (\ mathbf {Y} _ {1: m} | \ mathbf {X} _ {1: n}). pθenc, θdec (Y1: m ∣X1: n).
Кодер на основе трансформатора кодирует входную последовательность X1: n \ mathbf {X} _ {1: n} X1: n в последовательность из скрытых состояний X‾1: n \ mathbf {\ overline { X}} _ {1: n} X1: n, таким образом определяя отображение:
fθenc: X1: n → X‾1: n.f _ {\ theta _ {\ text {enc}}}: \ mathbf {X} _ {1: n} \ to \ mathbf {\ overline {X}} _ {1: n}. fθenc: X1: n → X1: n.
Часть декодера на основе трансформатора затем моделирует условное распределение вероятностей последовательности целевых векторов Y1: n \ mathbf {Y} _ {1: n} Y1: n с учетом последовательности закодированных скрытых состояний X‾1: n \ mathbf {\ overline {X}} _ {1: n} X1: n:
pθdec (Y1: n∣X‾1: n). p _ {\ theta_ {dec}} (\ mathbf {Y} _ {1: n} | \ mathbf {\ overline {X}} _ {1: n}). pθdec (Y1: n ∣X1: n ).
По правилу Байеса это распределение можно разложить на множители условное распределение вероятностей целевого вектора yi \ mathbf {y} _iyi учитывая закодированные скрытые состояния X‾1: n \ mathbf {\ overline {X}} _ {1: n} X1: n и все предыдущие целевые векторы Y0: i − 1 \ mathbf {Y} _ {0: i-1} Y0: i − 1:
pθdec (Y1: n∣X‾1: n) = ∏i = 1npθdec (yi∣Y0: i − 1, X‾1: n).{n} p _ {\ theta _ {\ text {dec}}} (\ mathbf {y} _i | \ mathbf {Y} _ {0: i-1}, \ mathbf {\ overline {X}} _ {1: n}). pθdec (Y1: n ∣X1: n) = i = 1∏n pθdec (yi ∣Y0: i − 1, X1: n).
Трансформаторный декодер тем самым отображает последовательность закодированных скрытых указывает X‾1: n \ mathbf {\ overline {X}} _ {1: n} X1: n и все предыдущие целевые векторы Y0: i − 1 \ mathbf {Y} _ {0: i-1} Y0: i − 1 в вектор logit li \ mathbf {l} _ili. Логит вектор li \ mathbf {l} _ili затем обрабатывается операцией softmax для определить условное распределение pθdec (yi∣Y0: i − 1, X‾1: n) p _ {\ theta _ {\ text {dec}}} (\ mathbf {y} _i | \ mathbf {Y} _ {0: i -1}, \ mathbf {\ overline {X}} _ {1: n}) pθdec (yi ∣Y0: i − 1, X1: n), так же, как это делается для декодеров на основе RNN.Однако в отличие от Декодеры на основе RNN, распределение целевого вектора yi \ mathbf {y} _iyi явно (или напрямую) обусловлено всеми предыдущими целевыми векторами y0,…, yi − 1 \ mathbf {y} _0, \ ldots, \ mathbf {y} _ {i-1} y0,…, yi − 1 Как мы увидим позже деталь. 0-й целевой вектор y0 \ mathbf {y} _0y0 настоящим представлен специальный "начало предложения" BOS \ text {BOS} вектор BOS.
Определив условное распределение pθdec (yi∣Y0: i − 1, X‾1: n) p _ {\ theta _ {\ text {dec}}} (\ mathbf {y} _i | \ mathbf {Y} _ {0 : i-1}, \ mathbf {\ overline {X}} _ {1: n}) pθdec (yi ∣Y0: i − 1, X1: n), теперь мы можем авторегрессивно сгенерировать вывод и таким образом определить отображение входной последовательности X1: n \ mathbf {X} _ {1: n} X1: n в выходную последовательность Y1: m \ mathbf {Y} _ {1: m} Y1: m при выводе.
Давайте визуализируем полный процесс авторегрессивной генерации модели кодеров-декодеров на базе трансформатора.
Трансформаторный энкодер окрашен в зеленый цвет, а Трансформаторный декодер окрашен в красный цвет. Как и в предыдущем разделе, мы показываем, как английское предложение «Я хочу купить машину», представленное как x1 = I \ mathbf {x} _1 = \ text {I} x1 = I, x2 = want \ mathbf {x} _2 = \ text { want} x2 = want, x3 = to \ mathbf {x} _3 = \ text {to} x3 = to, x4 = buy \ mathbf {x} _4 = \ text {buy} x4 = buy, x5 = a \ mathbf {x} _5 = \ text {a} x5 = a, x6 = car \ mathbf {x} _6 = \ text {car} x6 = car и x7 = EOS \ mathbf {x} _7 = \ text {EOS} x7 = EOS переводится на немецкий: "Ich will ein Auto kaufen "определяется как y0 = BOS \ mathbf {y} _0 = \ text {BOS} y0 = BOS, y1 = Ich \ mathbf {y} _1 = \ text {Ich} y1 = Ich, y2 = will \ mathbf {y} _2 = \ text {will} y2 = will, y3 = ein \ mathbf {y} _3 = \ text {ein} y3 = ein, y4 = Auto, y5 = kaufen \ mathbf {y} _4 = \ text {Auto}, \ mathbf {y} _5 = \ text {kaufen} y4 = Auto, y5 = kaufen и y6 = EOS \ mathbf {y} _6 = \ text {EOS} y6 = EOS.
Сначала кодировщик обрабатывает всю входную последовательность X1: 7 \ mathbf {X} _ {1: 7} X1: 7 = «Я хочу купить машину» (представлен светом зеленые векторы) в контекстуализированную кодированную последовательность X‾1: 7 \ mathbf {\ overline {X}} _ {1: 7} X1: 7. Например. x‾4 \ mathbf {\ overline {x}} _ 4x4 определяет кодировка, которая зависит не только от ввода x4 \ mathbf {x} _4x4 = "buy", но и все остальные слова «я», «хочу», «к», «а», «машина» и «EOS», , то есть контекст.
Затем входная кодировка X‾1: 7 \ mathbf {\ overline {X}} _ {1: 7} X1: 7 вместе с BOS вектор, i.е. y0 \ mathbf {y} _0y0, подается на декодер. Декодер обрабатывает входные данные X‾1: 7 \ mathbf {\ overline {X}} _ {1: 7} X1: 7 и y0 \ mathbf {y} _0y0, чтобы первый логит l1 \ mathbf {l} _1l1 (показан более темным красным) для определения условное распределение первого целевого вектора y1 \ mathbf {y} _1y1:
pθenc, dec (y∣y0, X1: 7) = pθenc, dec (y∣BOS, я хочу купить автомобиль EOS) = pθdec (y∣BOS, X‾1: 7). p _ {\ theta_ {enc, dec}} (\ mathbf {y} | \ mathbf {y} _0, \ mathbf {X} _ {1: 7}) = p _ {\ theta_ {enc, dec}} (\ mathbf {y} | \ text {BOS}, \ text {Я хочу купить машину EOS}) = p _ {\ theta_ {dec}} (\ mathbf {y} | \ text {BOS}, \ mathbf {\ overline { X}} _ {1: 7}).pθenc, dec (y∣y0, X1: 7) = pθenc, dec (y∣BOS, я хочу купить машину EOS) = pθdec (y∣BOS, X1: 7).
Затем выбирается первый целевой вектор y1 \ mathbf {y} _1y1 = Ich \ text {Ich} Ich из распределения (обозначено серыми стрелками) и теперь может быть снова подается на декодер. Теперь декодер обрабатывает как y0 \ mathbf {y} _0y0 = "BOS" и y1 \ mathbf {y} _1y1 = "Ich" для определения условного распределение второго целевого вектора y2 \ mathbf {y} _2y2:
pθdec (y∣BOS Ich, X‾1: 7). p _ {\ theta_ {dec}} (\ mathbf {y} | \ text {BOS Ich}, \ mathbf {\ overline {X}} _ {1: 7}).pθdec (y∣BOS Ich, X1: 7).
Мы можем снова выполнить выборку и создать целевой вектор y2 \ mathbf {y} _2y2 = "буду". Мы продолжаем в авторегрессивном режиме до тех пор, пока на шаге 6 не появится EOS. вектор выбирается из условного распределения:
EOS∼pθdec (y∣BOS Ich will ein Auto kaufen, X‾1: 7). \ text {EOS} \ sim p _ {\ theta_ {dec}} (\ mathbf {y} | \ text {BOS Ich будет ein Auto kaufen}, \ mathbf {\ overline {X}} _ {1: 7}). EOS∼pθdec (y∣BOS Ich будет ein Auto kaufen, X1: 7).
И так далее в авторегрессивном режиме.
Важно понимать, что энкодер используется только в первом прямой переход к карте X1: n \ mathbf {X} _ {1: n} X1: n в X‾1: n \ mathbf {\ overline {X}} _ {1: n} X1: n. Начиная со второго прямого прохода, декодер может напрямую использовать ранее рассчитанная кодировка X‾1: n \ mathbf {\ overline {X}} _ {1: n} X1: n. Для ясности, давайте проиллюстрируем первый и второй прямой проход для нашего пример выше.
Как видно, только на шаге i = 1i = 1i = 1 мы должны кодировать "Я хочу купить автомобиль EOS "на X‾1: 7 \ mathbf {\ overline {X}} _ {1: 7} X1: 7.На шаге i = 2i = 2i = 2 контекстные кодировки "Я хочу купить машину EOS" просто повторно используется декодером.
В 🤗Трансформаторах это авторегрессивное поколение выполняется под капотом.
при вызове метода .generate () . Воспользуемся одним из наших переводов
модели, чтобы увидеть это в действии.
из трансформаторов импортных MarianMTModel, MarianTokenizer
tokenizer = MarianTokenizer.from_pretrained («Хельсинки-НЛП / opus-mt-en-de»)
model = MarianMTModel.from_pretrained ("Хельсинки-НЛП / opus-mt-en-de")
input_ids = tokenizer («Я хочу купить машину», return_tensors = «pt»).input_ids
output_ids = model.generate (input_ids) [0]
печать (tokenizer.decode (output_ids))
Выход:
Ich will ein Auto kaufen
Вызов .generate () делает многие вещи скрытыми. Сначала проходит input_ids в кодировщик. Во-вторых, он передает предварительно определенный токен, которым является символ MarianMTModel вместе с закодированными input_ids для декодера.11. Более подробно о том, как работает декодирование с поиском луча, можно
посоветовал прочитать этот блог
Почта.
В приложение мы включили фрагмент кода, который показывает, как простая Метод генерации может быть реализован «с нуля». Чтобы полностью понять, как авторегрессивное поколение работает под капотом, это Настоятельно рекомендуется прочитать Приложение.
Подводя итог:
- Трансформаторный энкодер определяет отображение от входа последовательность X1: n \ mathbf {X} _ {1: n} X1: n в контекстуализированную последовательность кодирования X‾1: n \ mathbf {\ overline {X}} _ {1: n} X1: n.
- Трансформаторный декодер определяет условное распределение pθdec (yi∣Y0: i − 1, X‾1: n) p _ {\ theta _ {\ text {dec}}} (\ mathbf {y} _i | \ mathbf {Y} _ {0: i-1}, \ mathbf {\ overline {X}} _ {1: n}) pθdec (yi ∣Y0: i − 1, X1: n).
- При соответствующем механизме декодирования выходная последовательность Y1: m \ mathbf {Y} _ {1: m} Y1: m может автоматически выбираться из pθdec (yi∣Y0: i − 1, X‾1: n), ∀i∈ {1,…, m} p _ {\ theta _ {\ text {dec}}} (\ mathbf {y} _i | \ mathbf { Y} _ {0: i-1}, \ mathbf {\ overline {X}} _ {1: n}), \ forall i \ in \ {1, \ ldots, m \} pθdec (yi ∣ Y0: i − 1, X1: n), ∀i∈ {1,…, m}.
Отлично, теперь, когда мы получили общий обзор того, как
Модели кодировщиков-декодеров на базе трансформатора работают, мы можем глубже погрузиться в
как кодировщик, так и декодер части модели. В частности, мы
увидит, как именно кодировщик использует слой самовнимания
чтобы получить последовательность контекстно-зависимых векторных кодировок и как
Уровни самовнимания позволяют эффективно распараллеливать. Тогда мы будем
подробно объясните, как слой самовнимания работает в декодере
модель и как декодер зависит от выхода кодировщика с перекрестного внимания слоев для определения условного распределения pθdec (yi∣Y0: i − 1, X‾1: n) p _ {\ theta _ {\ text {dec}}} (\ mathbf {y} _i | \ mathbf { Y} _ {0: i-1}, \ mathbf {\ overline {X}} _ {1: n}) pθdec (yi ∣Y0: i − 1, X1: n).11 В случае "Helsinki-NLP / opus-mt-en-de" декодирование
параметры доступны
здесь,
где мы видим, что модель применяет поиск луча с num_beams = 6 .
Как упоминалось в предыдущем разделе, энкодер на базе трансформатора сопоставляет входную последовательность с контекстной последовательностью кодирования:
fθenc: X1: n → X‾1: n. 11.Двунаправленный Слой самовнимания помещает каждый входной вектор x′j, ∀j∈ {1,…, n} \ mathbf {x '} _ j, \ forall j \ in \ {1, \ ldots, n \} x′j, ∀j∈ {1,…, n} по отношению ко всем входные векторы x′1,…, x′n \ mathbf {x '} _ 1, \ ldots, \ mathbf {x'} _ nx′1,…, x′n и тем самым преобразует входной вектор x′j \ mathbf {x '} _ jx′j в более "изысканный" контекстное представление самого себя, определяемое как x′′j \ mathbf {x ''} _ jx′′j. Таким образом, первый блок кодера преобразует каждый входной вектор входная последовательность X1: n \ mathbf {X} _ {1: n} X1: n (показана светло-зеленым цветом ниже) из контекстно-независимое векторное представление в контекстно-зависимое векторное представление, и следующие блоки кодировщика дополнительно уточняют это контекстное представление до тех пор, пока последний блок кодировщика не выдаст окончательное контекстное кодирование X‾1: n \ mathbf {\ overline {X}} _ {1: n} X1: n (показано более темным зеленый внизу).22.
Наш примерный энкодер на базе трансформатора состоит из трех энкодеров. блоков, тогда как второй блок кодировщика показан более подробно в красный прямоугольник справа для первых трех входных векторов x1, x2andx3 \ mathbf {x} _1, \ mathbf {x} _2 и \ mathbf {x} _3x1, x2 иx3. Двунаправленный Механизм самовнимания проиллюстрирован полносвязным графом в показаны нижняя часть красного поля и два слоя прямой связи. в верхней части красного квадрата.Как было сказано ранее, мы сосредоточимся только на о двунаправленном механизме самовнимания.
Как видно, каждый выходной вектор слоя самовнимания x′′i, ∀i∈ {1,…, 7} \ mathbf {x ''} _ i, \ forall i \ in \ {1, \ ldots, 7 \} x′′i, ∀i∈ {1,…, 7} напрямую зависит от , от все входных вектора x′1,…, x′7 \ mathbf {x '} _ 1, \ ldots, \ mathbf {x'} _ 7x′1,…, x′7. Это означает, например , что входное векторное представление слова "хочу", то есть x′2 \ mathbf {x '} _ 2x′2, находится в прямой связи со словом "купить", я.е. x′4 \ mathbf {x '} _ 4x′4, но также со словом «I», то есть x′1 \ mathbf {x'} _ 1x′1. Выходное векторное представление «хочу», , то есть x′′2 \ mathbf {x ''} _ 2x′′2, таким образом, представляет собой более точную контекстную представление слова «хочу».
Давайте подробнее рассмотрим, как работает двунаправленное самовнимание. Каждый входной вектор x′i \ mathbf {x '} _ ix′i входной последовательности X′1: n \ mathbf {X'} _ {1: n} X′1: n блока кодера проецируется на ключевой вектор ki \ mathbf {k} _iki, вектор значений vi \ mathbf {v} _ivi и вектор запроса qi \ mathbf {q} _iqi (показаны ниже оранжевым, синим и фиолетовым соответственно) с помощью трех обучаемых весовых матриц Wq, Wv, Wk \ mathbf {W} _q, \ mathbf {W} _v, \ mathbf {W} _kWq, Wv, Wk:
qi = Wqx′i, \ mathbf {q} _i = \ mathbf {W} _q \ mathbf {x '} _ i, qi = Wq x′i, vi = Wvx′i, \ mathbf {v} _i = \ mathbf {W} _v \ mathbf {x '} _ i, vi = Wv x′i, ki = Wkx′i, \ mathbf {k} _i = \ mathbf {W} _k \ mathbf {x '} _ i, ki = Wk x′i, ∀i∈ {1,… n}.\ forall i \ in \ {1, \ ldots n \}. ∀i∈ {1,… n}.
Обратите внимание, что одинаковые весовые матрицы применяются к каждому входному вектору xi, ∀i∈ {i,…, n} \ mathbf {x} _i, \ forall i \ in \ {i, \ ldots, n \} xi, ∀i∈ {i,…, n}. После проецирования каждого входной вектор xi \ mathbf {x} _ixi в вектор запроса, ключа и значения, каждый вектор запроса qj, ∀j∈ {1,…, n} \ mathbf {q} _j, \ forall j \ in \ {1, \ ldots, n \} qj, ∀j∈ {1,…, n} равен в сравнении ко всем ключевым векторам k1,…, kn \ mathbf {k} _1, \ ldots, \ mathbf {k} _nk1,…, kn. Чем больше похожий один из ключевых векторов k1,… kn \ mathbf {k} _1, \ ldots \ mathbf {k} _nk1,… kn должен вектор запроса qj \ mathbf {q} _jqj, тем важнее соответствующий вектор значений vj \ mathbf {v} _jvj для выходного вектора x′′j \ mathbf {x ''} _ jx′′j.\ intercal \ mathbf {q} _j) Softmax (K1: n⊺ qj) как показано в уравнении ниже. Для полного описания слой самовнимания, читателю рекомендуется взглянуть на это сообщение в блоге или исходная бумага.
Хорошо, это звучит довольно сложно. Проиллюстрируем
двунаправленный слой самовнимания для одного из векторов запросов нашего
пример выше. Для простоты предполагается, что наш примерный
Декодер на базе трансформатора использует только одну головку внимания конфиг.num_heads = 1 и что нормализация не применяется.
Слева показан ранее проиллюстрированный второй блок кодера. снова и справа, детальная визуализация двунаправленного Механизм самовнимания дан для второго входного вектора x′2 \ mathbf {x '} _ 2x′2, который соответствует входному слову «хочу». Вначале проецируются все входные векторы x′1,…, x′7 \ mathbf {x '} _ 1, \ ldots, \ mathbf {x'} _ 7x′1,…, x′7 к соответствующим векторам запросов q1,…, q7 \ mathbf {q} _1, \ ldots, \ mathbf {q} _7q1,…, q7 (вверху фиолетовым цветом показаны только первые три вектора запроса), значение векторы v1,…, v7 \ mathbf {v} _1, \ ldots, \ mathbf {v} _7v1,…, v7 (показаны синим) и ключ векторы k1,…, k7 \ mathbf {k} _1, \ ldots, \ mathbf {k} _7k1,…, k7 (показаны оранжевым).{\ intercal} K1: 7⊺ и q2 \ mathbf {q} _2q2, таким образом, делает его можно сравнить векторное представление "хочу" со всеми другими входные векторные представления «Я», «К», «Купить», «А», «Автомобиль», "EOS", чтобы веса самовнимания отражали важность каждого из другие входные векторные представления x′j, с j ≠ 2 \ mathbf {x '} _ j \ text {, с} j \ ne 2x′j, с j = 2 для уточненного представления x′′2 \ mathbf { x ''} _ 2x′′2 слова «хочу».
Чтобы лучше понять значение двунаправленного слой самовнимания, предположим, что следующее предложение обрабатывается: « Дом красивый и удачно расположенный в центре города. где легко добраться на общественном транспорте ».Слово "это" относится к «дому», который находится на расстоянии 12 «позиций». В энкодеры на основе трансформаторов, двунаправленный слой самовнимания выполняет одну математическую операцию, чтобы поместить входной вектор "дом" во взаимосвязи с входным вектором "оно" (сравните с первая иллюстрация этого раздела). Напротив, в RNN на основе кодировщик, слово, которое находится на расстоянии 12 "позиций", потребует не менее 12 математические операции, означающие, что в кодировщике на основе RNN линейный количество математических операций не требуется.Это делает его много кодировщику на основе RNN сложнее моделировать контекстные представления. Также становится ясно, что энкодер на основе трансформатора гораздо менее склонен к потере важной информации, чем основанный на RNN модель кодировщика-декодера, поскольку длина последовательности кодирования равна оставил то же самое, , т.е. len (X1: n) = len (X‾1: n) = n \ textbf {len} (\ mathbf {X} _ {1: n}) = \ textbf {len} (\ mathbf {\ overline {X}} _ {1: n}) = nlen (X1: n) = len (X1: n) = n, в то время как RNN сжимает длину из ∗ len ((X1: n) = n * \ textbf {len} ((\ mathbf {X} _ {1: n}) = n ∗ len ((X1: n) = n просто len (c) = 1 \ textbf {len} (\ mathbf {c}) = 1len (c) = 1, что очень затрудняет работу RNN для эффективного кодирования дальнодействующих зависимостей между входными словами.\ intercal \ mathbf {K} _ {1: n}) + \ mathbf {X '} _ {1: n}. X′′1: n = V1: n Softmax (Q1: n⊺ K1: n) + X′1: n.
Выходные данные X′′1: n = x′′1,…, x′′n \ mathbf {X ''} _ {1: n} = \ mathbf {x ''} _ 1, \ ldots, \ mathbf { x ''} _ nX′′1: n = x′′1,…, x′′n вычисляется с помощью серии умножений матриц и softmax операция, которую можно эффективно распараллелить. Обратите внимание, что в Модель кодировщика на основе RNN, вычисление скрытого состояния c \ mathbf {c} c должно выполняться последовательно: вычисление скрытого состояния первый входной вектор x1 \ mathbf {x} _1x1, затем вычислить скрытое состояние второй входной вектор, который зависит от скрытого состояния первого скрытого вектор и др.Последовательный характер RNN не позволяет эффективно распараллеливание и делает их более неэффективными по сравнению с модели кодировщиков на базе трансформаторов на современном оборудовании GPU.
Отлично, теперь мы должны лучше понять а) как модели кодировщиков на основе трансформаторов эффективно моделируют контекстные представления и б) как они эффективно обрабатывают длинные последовательности входные векторы.
Теперь давайте напишем небольшой пример кодирующей части нашего MarianMT модели кодировщика-декодера для проверки того, что объясненная теория
выполняется на практике.11 Подробное объяснение роли слоев прямой связи
в трансформаторных моделях выходит за рамки этого ноутбука. это
утверждал в Yun et. al, (2017)
что уровни прямой связи имеют решающее значение для сопоставления каждого контекстного вектора x′i \ mathbf {x '} _ ix′i индивидуально с желаемым выходным пространством, которое самовнимание слой самостоятельно не справляется. Должен быть
здесь отмечено, что каждый выходной токен x ′ \ mathbf {x '} x ′ обрабатывается
тот же слой прямой связи. Подробнее читателю рекомендуется прочитать
бумага.22 Однако входной вектор EOS необязательно добавлять к
входная последовательность, но, как было показано, во многих случаях улучшает производительность.
В отличие от 0-го BOS \ text {BOS} целевой вектор BOS
декодер на основе трансформатора требуется как начальный входной вектор для
предсказать первый целевой вектор.
из трансформаторов импортных MarianMTModel, MarianTokenizer
импортный фонарик
tokenizer = MarianTokenizer.from_pretrained («Хельсинки-НЛП / opus-mt-en-de»)
модель = MarianMTModel.from_pretrained ("Хельсинки-НЛП / opus-mt-en-de")
вложения = модель.get_input_embeddings ()
input_ids = tokenizer («Я хочу купить машину», return_tensors = «pt»). input_ids
encoder_hidden_states = model.base_model.encoder (input_ids, return_dict = True) .last_hidden_state
input_ids_perturbed = tokenizer («Я хочу купить дом», return_tensors = «pt»). input_ids
encoder_hidden_states_perturbed = model.base_model.encoder (input_ids_perturbed, return_dict = True) .last_hidden_state
print (f "Длина вложений ввода {вложений (input_ids).форма [1]}. Длина encoder_hidden_states {encoder_hidden_states.shape [1]} ")
print ("Кодировка для` I` равна его возмущенной версии ?: ", torch.allclose (encoder_hidden_states [0, 0], encoder_hidden_states_perturbed [0, 0], atol = 1e-3))
Выходы:
Длина вложений ввода 7. Длина encoder_hidden_states 7
Кодировка для `I` равна его возмущенной версии ?: False
Сравниваем длину вложений входного слова, i.е. вложений (input_ids) , соответствующих X1: n \ mathbf {X} _ {1: n} X1: n, с
длина encoder_hidden_states , соответствующая X‾1: n \ mathbf {\ overline {X}} _ {1: n} X1: n. Кроме того, мы переадресовали последовательность слов
«Хочу купить машину» и слегка возмущенный вариант «Хочу
купить дом "через кодировщик, чтобы проверить, есть ли первая выходная кодировка,
соответствует «I», отличается, когда в
входная последовательность.
Как и ожидалось, выходная длина вложений входного слова и кодировщика выходные кодировки, i.е. len (X1: n) \ textbf {len} (\ mathbf {X} _ {1: n}) len (X1: n) и len (X‾1: n) \ textbf {len} (\ mathbf { \ overline {X}} _ {1: n}) len (X1: n), равно. Во-вторых, это может быть отметил, что значения закодированного выходного вектора x‾1 = "I" \ mathbf {\ overline {x}} _ 1 = \ text {"I"} x1 = "I" отличаются, когда последнее слово меняется с "автомобиль" на "дом". Однако это не должно вызывать сюрприз, если кто-то понял двунаправленное самовнимание.
Кстати, модели с автокодированием , такие как BERT, имеют точно такие же Архитектура как на базе трансформатора модели кодировщика . Автокодирование модели используют эту архитектуру для массового самоконтроля предварительное обучение текстовых данных в открытом домене, чтобы они могли сопоставить любое слово последовательность к глубокому двунаправленному представлению. В Devlin et al. (2018) авторы показывают, что предварительно обученная модель BERT с одним классификационным слоем для конкретной задачи сверху может достичь результатов SOTA по одиннадцати задачам НЛП. Все автокодирование модели 🤗Трансформаторов можно найти здесь.
ДекодерКак упоминалось в разделе Кодер-декодер , преобразователь на основе преобразователя декодер определяет условное распределение вероятностей цели последовательность с учетом контекстуализированной кодирующей последовательности:
pθdec (Y1: m∣X‾1: n), p _ {\ theta_ {dec}} (\ mathbf {Y} _ {1: m} | \ mathbf {\ overline {X}} _ {1: n} ), pθdec (Y1: m ∣X1: n),
, который по правилу Байеса можно разложить на произведение условного распределения следующего целевого вектора с учетом контекстуализированного кодирующая последовательность и все предыдущие целевые векторы:
pθdec (Y1: m∣X‾1: n) = ∏i = 1mpθdec (yi∣Y0: i − 1, X‾1: n).{m} p _ {\ theta_ {dec}} (\ mathbf {y} _i | \ mathbf {Y} _ {0: i-1}, \ mathbf {\ overline {X}} _ {1: n}). pθdec (Y1: m ∣X1: n) = i = 1∏m pθdec (yi ∣Y0: i − 1, X1: n).
Давайте сначала разберемся, как декодер на основе трансформатора определяет распределение вероятностей. Трансформаторный декодер представляет собой набор блоки декодера , за которыми следует плотный слой, «голова LM». Стек блоков декодера сопоставляет контекстуализированную последовательность кодирования X‾1: n \ mathbf {\ overline {X}} _ {1: n} X1: n и последовательность целевого вектора с добавлением вектор BOS \ text {BOS} BOS и переход к последнему целевому вектору i.е. Y0: i − 1 \ mathbf {Y} _ {0: i-1} Y0: i − 1, в закодированную последовательность целевых векторов Y‾0: i − 1 \ mathbf {\ overline {Y}} _ {0: i-1} Y0: i-1. Затем «голова LM» отображает закодированные последовательность целевых векторов Y‾0: i − 1 \ mathbf {\ overline {Y}} _ {0: i-1} Y0: i − 1 до a последовательность логит-векторов L1: n = l1,…, ln \ mathbf {L} _ {1: n} = \ mathbf {l} _1, \ ldots, \ mathbf {l} _nL1: n = l1,…, ln, тогда как размерность каждого логит-вектора li \ mathbf {l} _ili соответствует размер словарного запаса. Таким образом, для каждого i∈ {1,…, n} i \ in \ {1, \ ldots, n \} i∈ {1,…, n} a распределение вероятностей по всему словарю может быть получено с помощью применение операции softmax к li \ mathbf {l} _ili. {\ intercal} \ mathbf {\ overline {y}} _ {i-1 }) = Softmax (Wemb⊺ y i − 1) = Softmax (li).= \ text {Softmax} (\ mathbf {l} _i). = Softmax (li).
Собираем все вместе, чтобы смоделировать условное распределение последовательности целевых векторов Y1: m \ mathbf {Y} _ {1: m} Y1: m, целевые векторы Y1: m − 1 \ mathbf {Y} _ {1: m-1} Y1: m − 1 Добавляется специальным вектором BOS \ text {BOS} BOS, , то есть y0 \ mathbf {y} _0y0, сначала отображаются вместе с контекстуализированными кодирующая последовательность X‾1: n \ mathbf {\ overline {X}} _ {1: n} X1: n в вектор логита последовательность L1: m \ mathbf {L} _ {1: m} L1: m. Следовательно, каждый целевой вектор логита li \ mathbf {l} _ili преобразуется в условную вероятность распределение целевого вектора yi \ mathbf {y} _iyi с использованием softmax операция.{m} p _ {\ theta_ {dec}} (\ mathbf {y} _i | \ mathbf {Y} _ {0: i-1}, \ mathbf {\ overline {X}} _ {1: n}). pθdec (Y1: m ∣X1: n) = i = 1∏m pθdec (yi ∣Y0: i − 1, X1: n).
В отличие от трансформаторных энкодеров, в трансформаторных декодеры, закодированный выходной вектор y‾i \ mathbf {\ overline {y}} _ iy i должен быть хорошее представление следующего целевого вектора yi + 1 \ mathbf {y} _ {i + 1} yi + 1 и не самого входного вектора. Кроме того, закодированный выходной вектор y‾i \ mathbf {\ overline {y}} _ iy i должен быть обусловлен всеми контекстными кодирующая последовательность X‾1: n \ mathbf {\ overline {X}} _ {1: n} X1: n.22. Слой однонаправленного самовнимания. ставит каждый из своих входных векторов y′j \ mathbf {y '} _ jy′j только во взаимосвязь с все предыдущие входные векторы y′i, с i≤j \ mathbf {y '} _ i, \ text {with} i \ le jy′i, с i≤j для все j∈ {1,…, n} j \ in \ {1, \ ldots, n \} j∈ {1,…, n} для моделирования распределения вероятностей следующие целевые векторы. Слой перекрестного внимания помещает каждый из входные векторы y′′j \ mathbf {y ''} _ jy′′j во взаимосвязи со всеми контекстуализированными кодирующие векторы X‾1: n \ mathbf {\ overline {X}} _ {1: n} X1: n, чтобы обусловить распределение вероятностей следующих целевых векторов на входе кодировщик тоже.
Хорошо, давайте визуализируем декодер на основе трансформатора для нашего Пример перевода с английского на немецкий.
Мы видим, что декодер отображает вход Y0: 5 \ mathbf {Y} _ {0: 5} Y0: 5 "BOS", «Ich», «will», «ein», «Auto», «kaufen» (показаны светло-красным) вместе с контекстуализированной последовательностью «я», «хочу», «к», «купить», «а», «автомобиль», «EOS», т.е. X‾1: 7 \ mathbf {\ overline {X}} _ {1: 7} X1: 7 (показано темно-зеленым) в векторы логита L1: 6 \ mathbf {L} _ {1: 6} L1: 6 (показано на темно-красный).
Применение операции softmax к каждому l1, l2,…, l5 \ mathbf {l} _1, \ mathbf {l} _2, \ ldots, \ mathbf {l} _5l1, l2,…, l5 может таким образом определить условные распределения вероятностей:
pθdec (y∣BOS, X‾1: 7), p _ {\ theta_ {dec}} (\ mathbf {y} | \ text {BOS}, \ mathbf {\ overline {X}} _ {1: 7} ), pθdec (y∣BOS, X1: 7), pθdec (y∣BOS Ich, X‾1: 7), p _ {\ theta_ {dec}} (\ mathbf {y} | \ text {BOS Ich}, \ mathbf {\ overline {X}} _ {1: 7 }), pθdec (y∣BOS Ich, X1: 7), …, \ Ldots,…, pθdec (y∣BOS Ich будет ein Auto kaufen, X‾1: 7). p _ {\ theta_ {dec}} (\ mathbf {y} | \ text {BOS Ich будет ein Auto kaufen}, \ mathbf {\ overline {X}} _ {1: 7}).pθdec (y∣BOS Ich будет ein Auto kaufen, X1: 7).
Общая условная вероятность:
pθdec (Ich будет ein Auto kaufen EOS∣X‾1: n) p _ {\ theta_ {dec}} (\ text {Ich будет ein Auto kaufen EOS} | \ mathbf {\ overline {X}} _ {1: n }) pθdec (Ich будет ein Auto kaufen EOS∣X1: n)
Следовательно,может быть вычислено как следующее произведение:
pθdec (Ich∣BOS, X‾1: 7) ×… × pθdec (EOS∣BOS Ich будет ein Auto kaufen, X‾1: 7). p _ {\ theta_ {dec}} (\ text {Ich} | \ text {BOS}, \ mathbf {\ overline {X}} _ {1: 7}) \ times \ ldots \ times p _ {\ theta_ {dec} } (\ text {EOS} | \ text {BOS Ich будет ein Auto kaufen}, \ mathbf {\ overline {X}} _ {1: 7}).pθdec (Ich∣BOS, X1: 7) ×… × pθdec (EOS∣BOS Ich будет использовать Auto kaufen, X1: 7).
В красном поле справа показан блок декодера для первых трех целевые векторы y0, y1, y2 \ mathbf {y} _0, \ mathbf {y} _1, \ mathbf {y} _2y0, y1, y2. В нижнем части, механизм однонаправленного самовнимания проиллюстрирован и в в центре проиллюстрирован механизм перекрестного внимания. Давай сначала сосредоточьтесь на однонаправленном самовнимании.
Как при двунаправленном самовнимании, при однонаправленном самовнимании, векторы запросов q0,…, qm − 1 \ mathbf {q} _0, \ ldots, \ mathbf {q} _ {m-1} q0,…, qm − 1 (показаны на фиолетовый внизу), ключевые векторы k0,…, km − 1 \ mathbf {k} _0, \ ldots, \ mathbf {k} _ {m-1} k0,…, km − 1 (показаны оранжевым ниже), и векторы значений v0,…, vm − 1 \ mathbf {v} _0, \ ldots, \ mathbf {v} _ {m-1} v0,…, vm − 1 (показаны на синий ниже) проецируются из соответствующих входных векторов y′0,…, y′m − 1 \ mathbf {y '} _ 0, \ ldots, \ mathbf {y'} _ {m-1} y′0,…, y′m −1 (показано светло-красным цветом ниже).Однако при однонаправленном самовнимании каждый вектор запроса qi \ mathbf {q} _iqi сравнивается только с его соответствующим ключевым вектором и все предыдущие, а именно k0,…, ki \ mathbf {k} _0, \ ldots, \ mathbf {k} _ik0,…, ki, чтобы получить соответствующие веса внимания . Это предотвращает включение любой информации в выходной вектор y′′j \ mathbf {y ''} _ jy′′j (показан темно-красным ниже) о следующем входном векторе yi, с i> j \ mathbf {y} _i, \ text {с} i> jyi, с i> j для все j∈ {0,…, m − 1} j \ in \ {0, \ ldots, m - 1 \} j∈ {0,…, m − 1}.\ intercal \ mathbf {q} _i) + \ mathbf {y '} _ i. y′′i = V0: i Softmax (K0: i⊺ qi) + y′i.
Обратите внимание, что диапазон индекса векторов ключей и значений равен 0: i0: i0: i вместо 0: m − 10: m-10: m − 1, который будет диапазоном ключевых векторов в двунаправленное самовнимание.
Давайте проиллюстрируем однонаправленное самовнимание для входного вектора y′1 \ mathbf {y '} _ 1y′1 для нашего примера выше.
Как видно, y′′1 \ mathbf {y ''} _ 1y′′1 зависит только от y′0 \ mathbf {y '} _ 0y′0 и y′1 \ mathbf {y'} _ 1y′1 .Поэтому положим векторное представление слова «Ich», т.е. y′1 \ mathbf {y '} _ 1y′1 только в отношении самого себя и Целевой вектор "BOS", то есть y′0 \ mathbf {y '} _ 0y′0, но не с векторное представление слова «будет», т.е. y′2 \ mathbf {y '} _ 2y′2.
Итак, почему так важно, чтобы мы использовали однонаправленное самовнимание в декодер вместо двунаправленного самовнимания? Как указано выше, декодер на основе трансформатора определяет отображение из последовательности ввода вектор Y0: m − 1 \ mathbf {Y} _ {0: m-1} Y0: m − 1 в логиты, соответствующие следующему входные векторы декодера, а именно L1: m \ mathbf {L} _ {1: m} L1: m.В нашем примере это означает например , что отображен входной вектор y1 \ mathbf {y} _1y1 = "Ich" в вектор логита l2 \ mathbf {l} _2l2, который затем используется для прогнозирования входной вектор y2 \ mathbf {y} _2y2. Таким образом, если y′1 \ mathbf {y '} _ 1y′1 будет иметь доступ к следующим входным векторам Y′2: 5 \ mathbf {Y '} _ {2: 5} Y′2: 5, декодер будет просто скопируйте векторное представление «воли», , т.е. y′2 \ mathbf {y '} _ 2y′2, чтобы получить его выход y′′1 \ mathbf {y' '} _ 1y′′1. Это было бы перенаправлен на последний уровень, так что закодированный выходной вектор y‾1 \ mathbf {\ overline {y}} _ 1y 1 по существу просто соответствовал бы векторное представление y2 \ mathbf {y} _2y2.
Это явно невыгодно, поскольку декодер на основе трансформатора никогда не учись предсказывать следующее слово, учитывая все предыдущие слова, а просто скопируйте целевой вектор yi \ mathbf {y} _iyi через сеть в y‾i − 1 \ mathbf {\ overline {y}} _ {i-1} y i − 1 для всех i∈ {1,… , m} i \ in \ {1, \ ldots, m \} i∈ {1,…, m}. В чтобы определить условное распределение следующего целевого вектора, распределение не может быть обусловлено следующим целевым вектором. Нет смысла предсказывать yi \ mathbf {y} _iyi из p (y∣Y0: i, X‾) p (\ mathbf {y} | \ mathbf {Y} _ {0: i}, \ mathbf {\ overline {X}}) p (y∣Y0: i, X), поскольку распределение обусловлено целевым вектором, который предполагается модель.Следовательно, однонаправленная архитектура самовнимания позволяет нам определить вероятностное распределение причинно-следственных связей , которое необходимо для эффективного моделирования условного распределения следующих целевой вектор.
Отлично! Теперь мы можем перейти к слою, который соединяет кодировщик и декодер - механизм перекрестного внимания !
Слой перекрестного внимания принимает в качестве входных данных две векторные последовательности: выходы однонаправленного слоя самовнимания, i.е. Y′′0: m − 1 \ mathbf {Y ''} _ {0: m-1} Y′′0: m − 1 и контекстуализированные векторы кодирования X‾1: n \ mathbf {\ overline {X }} _ {1: n} X1: n. Как и в слое самовнимания, запрос векторы q0,…, qm − 1 \ mathbf {q} _0, \ ldots, \ mathbf {q} _ {m-1} q0,…, qm − 1 являются проекциями выходные векторы предыдущего слоя, , то есть Y′′0: m − 1 \ mathbf {Y ''} _ {0: m-1} Y′′0: m − 1. Однако векторы ключа и значения k0,…, km − 1 \ mathbf {k} _0, \ ldots, \ mathbf {k} _ {m-1} k0,…, km − 1 и v0,…, vm −1 \ mathbf {v} _0, \ ldots, \ mathbf {v} _ {m-1} v0,…, vm − 1 - проекции контекстуализированные векторы кодирования X‾1: n \ mathbf {\ overline {X}} _ {1: n} X1: n.Имея определены векторы ключа, значения и запроса, вектор запроса qi \ mathbf {q} _iqi затем сравниваются с все ключевых вектора и используется соответствующая оценка для взвешивания соответствующих векторов значений, как и в случае двунаправленное самовнимание, чтобы дать выходной вектор y ′ ′ ′ i \ mathbf {y '' '} _ iy ′ ′ ′ i для всех i∈0,…, m − 1i \ in {0, \ ldots , m-1} i∈0,…, m − 1. \ intercal \ mathbf {q} _i) + \ mathbf {y ''} _ я.y ′ ′ ′ i = V1: n Softmax (K1: n⊺ qi) + y′′i.
Обратите внимание, что диапазон индекса векторов ключей и значений равен 1: n1: n1: n соответствует количеству контекстуализированных векторов кодирования.
Давайте визуализируем механизм перекрестного внимания Давайте для ввода вектор y′′1 \ mathbf {y ''} _ 1y′′1 для нашего примера выше.
Мы видим, что вектор запроса q1 \ mathbf {q} _1q1 (показан фиолетовым цветом) равен получено из y′′1 \ mathbf {y ''} _ 1y′′1 (показано красным) и, следовательно, полагается на вектор представление слова «Ич».Вектор запроса q1 \ mathbf {q} _1q1 затем сравнивается с ключевыми векторами k1,…, k7 \ mathbf {k} _1, \ ldots, \ mathbf {k} _7k1,…, k7 (показаны желтым), соответствующими представление контекстного кодирования всех входных векторов кодировщика X1: n \ mathbf {X} _ {1: n} X1: n = "Я хочу купить автомобиль EOS". Это ставит вектор представление "Ich" в прямую связь со всеми входами кодировщика векторы. Наконец, веса внимания умножаются на значение векторы v1,…, v7 \ mathbf {v} _1, \ ldots, \ mathbf {v} _7v1,…, v7 (показаны бирюзовым) в вывести в дополнение к входному вектору y′′1 \ mathbf {y ''} _ 1y′′1 выходной вектор y ′ ′ ′ 1 \ mathbf {y '' '} _ 1y ′ ′ ′ 1 (показан темно-красным ).
Итак, интуитивно, что именно здесь происходит? Каждый выходной вектор y ′ ′ ′ i \ mathbf {y '' '} _ iy ′ ′ ′ i является взвешенной суммой всех проекций значений входы кодировщика v1,…, v7 \ mathbf {v} _ {1}, \ ldots, \ mathbf {v} _7v1,…, v7 плюс вход вектор y′′i \ mathbf {y ''} _ iy′′i ( см. формулу , проиллюстрированную выше). Ключ механизм понимания следующий: в зависимости от того, насколько похож проекция запроса входного вектора декодера qi \ mathbf {q} _iqi на проекция ключа входного вектора кодировщика kj \ mathbf {k} _jkj, тем более важна проекция значения входного вектора кодировщика vj \ mathbf {v} _jvj.В общих чертах это означает, что чем больше «родственный» входное представление декодера относится к входному представлению кодировщика, больше влияет ли входное представление на выход декодера представление.
Круто! Теперь мы можем видеть, как эта архитектура хорошо обрабатывает каждый вывод. вектор y ′ ′ ′ i \ mathbf {y '' '} _ iy ′ ′ ′ i на взаимодействии между входом кодировщика векторы X‾1: n \ mathbf {\ overline {X}} _ {1: n} X1: n и входной вектор y′′i \ mathbf {y ''} _ iy′′i. Еще одно важное наблюдение на этом этапе заключается в том, что архитектура полностью не зависит от количества nnn контекстуализированные векторы кодирования X‾1: n \ mathbf {\ overline {X}} _ {1: n} X1: n, на которых выходной вектор y ′ ′ ′ i \ mathbf {y '' '} _ iy ′ ′ ′ i обусловлен.{\ text {cross}} _ {v} Wvcross для получения ключевых векторов k1,…, kn \ mathbf {k} _1, \ ldots, \ mathbf {k} _nk1,…, kn и векторов значений v1 ,…, Vn \ mathbf {v} _1, \ ldots, \ mathbf {v} _nv1,…, vn соответственно используются всеми позиции 1,…, n1, \ ldots, n1,…, n и все векторы значений v1,…, vn \ mathbf {v} _1, \ ldots, \ mathbf {v} _n v1,…, vn суммируются к одному взвешенный усредненный вектор. Теперь также становится очевидным, почему декодер на основе трансформатора не страдает зависимостью от дальнего действия Проблема, от которой страдает декодер на основе RNN.Потому что каждый декодер логит вектор напрямую зависит от каждого отдельного закодированного выходного вектора, количество математических операций для сравнения первого закодированного выходной вектор и последний логит-вектор декодера составляют по существу только один.
В заключение, однонаправленный слой самовнимания отвечает за согласование каждого выходного вектора со всеми предыдущими входными векторами декодера а текущий вектор ввода и слой перекрестного внимания - отвечает за дальнейшее кондиционирование каждого выходного вектора на всех закодированных входных данных. векторы.22 Опять же, подробное объяснение роли прямого игра слоев в моделях на основе трансформатора выходит за рамки этого ноутбук. Это утверждается в Yun et. аль, (2017), что слои с прямой связью имеют решающее значение для сопоставления каждого контекстного вектора x′i \ mathbf {x '} _ ix′i индивидуально в желаемое пространство вывода, которое слой самовнимания не может справиться самостоятельно. Здесь следует отметить, что каждый выходной токен x '\ mathbf {x'} x 'обрабатывается одним и тем же уровнем прямой связи. Для большего Подробности, читателю рекомендуется прочитать статью.
из трансформаторов импортных MarianMTModel, MarianTokenizer
импортный фонарик
tokenizer = MarianTokenizer.from_pretrained («Хельсинки-НЛП / opus-mt-en-de»)
model = MarianMTModel.from_pretrained ("Хельсинки-НЛП / opus-mt-en-de")
вложения = модель.get_input_embeddings ()
input_ids = tokenizer («Я хочу купить машину», return_tensors = «pt»). input_ids
decoder_input_ids = tokenizer (" Ich will ein", return_tensors = "pt", add_special_tokens = False) .input_ids
decoder_output_vectors = модель.base_model.decoder (decoder_input_ids) .last_hidden_state
lm_logits = torch.nn.functional.linear (decoder_output_vectors, embeddings.weight, bias = model.final_logits_bias)
decoder_input_ids_perturbed = tokenizer (" Ich will das", return_tensors = "pt", add_special_tokens = False) .input_ids
decoder_output_vectors_perturbed = model.base_model.decoder (decoder_input_ids_perturbed) .last_hidden_state
lm_logits_perturbed = torch.nn.functional.linear (decoder_output_vectors_perturbed, embeddings.weight, bias = model.final_logits_bias)
print (f "Форма входных векторов декодера {embeddings (decoder_input_ids) .shape}. Форма логитов декодера {lm_logits.shape}")
print ("Кодировка для` Ich` равна его измененной версии ?: ", torch.allclose (lm_logits [0, 0], lm_logits_perturbed [0, 0], atol = 1e-3))
Выход:
Форма входных векторов декодера torch.Size ([1, 5, 512]). Форма декодера logits torch.Size ([1, 5, 58101])
Кодировка для `Ich` равна его измененной версии ?: True
Мы сравниваем выходную форму вложений входных слов декодера, i.е. вложений (decoder_input_ids) (соответствует Y0: 4 \ mathbf {Y} _ {0: 4} Y0: 4,
здесь соответствует BOS, а «Ich will das» токенизируется до 4
токены) с размерностью lm_logits (соответствует L1: 5 \ mathbf {L} _ {1: 5} L1: 5). Также мы передали последовательность слов
" Ich will das" и слегка возмущенная версия
" Ich will das" вместе с encoder_output_vectors через кодировщик, чтобы проверить, есть ли второй lm_logit , соответствующий «Ich», отличается, когда только последнее слово
изменено во входной последовательности («ein» -> «das»).
Как и ожидалось, выходные формы вложений входных слов декодера и
lm_logits, , т.е. размерность Y0: 4 \ mathbf {Y} _ {0: 4} Y0: 4 и L1: 5 \ mathbf {L} _ {1: 5} L1: 5 в последнем измерение. В то время как
длина последовательности такая же (= 5), размерность входа декодера
вложение слов соответствует model.config.hidden_size , тогда как
размерность lm_logit соответствует размеру словаря model.config.vocab_size , как описано выше.Во-вторых, можно отметить
что значения закодированного выходного вектора l1 = "Ich" \ mathbf {l} _1 = \ text {"Ich"} l1 = "Ich" совпадают при изменении последнего слова
от «эйн» до «дас». Однако это не должно вызывать удивления, если
человек понял однонаправленное самовнимание.
В заключение отметим, что модели с авторегрессией , такие как GPT2, имеют та же архитектура, что и на базе трансформатора модели декодера если один удаляет слой перекрестного внимания, потому что автономный авторегрессивный модели не привязаны к каким-либо выходам энкодера.Так авторегрессивный модели по сути такие же, как модели с автоматическим кодированием , но заменяют двунаправленное внимание с однонаправленным вниманием. Эти модели также можно предварительно обучить работе с массивными текстовыми данными в открытом домене, чтобы показывать впечатляющая производительность в задачах генерации естественного языка (NLG). В Radford et al. (2019), авторы показывают, что предварительно обученная модель GPT2 может достичь SOTA или закрыть к результатам SOTA при выполнении различных задач NLG без особой настройки. Все авторегрессивные модели 🤗Трансформаторов можно найти здесь.
Хорошо, вот и все! Теперь вы должны хорошо понимать модели кодеров-декодеров на базе трансформатора и как их использовать с 🤗Библиотека трансформеров.
Большое спасибо Виктору Саню, Саше Рашу, Сэму Шлейферу, Оливеру Остранду, Теду Московицу и Кристиану Кивику за ценные отзывы.
Приложение Как упоминалось выше, следующий фрагмент кода показывает, как можно программировать
простой метод генерации кодера-декодера на базе трансформатора модели.Здесь мы реализуем простой метод декодирования жадного , используя torch.argmax для выборки целевого вектора.
из трансформаторов импортных MarianMTModel, MarianTokenizer
импортный фонарик
tokenizer = MarianTokenizer.from_pretrained («Хельсинки-НЛП / opus-mt-en-de»)
model = MarianMTModel.from_pretrained ("Хельсинки-НЛП / opus-mt-en-de")
input_ids = tokenizer («Я хочу купить машину», return_tensors = «pt»). input_ids
decoder_input_ids = tokenizer ("", add_special_tokens = False, return_tensors = "pt").input_ids
assert decoder_input_ids [0, 0] .item () == model.config.decoder_start_token_id, "` decoder_input_ids` должен соответствовать `model.config.decoder_start_token_id`"
output = model (input_ids, decoder_input_ids = decoder_input_ids, return_dict = True)
encoded_sequence = (outputs.encoder_last_hidden_state,)
lm_logits = outputs.logits
next_decoder_input_ids = torch.argmax (lm_logits [:, -1:], ось = -1)
decoder_input_ids = torch.cat ([decoder_input_ids, next_decoder_input_ids], axis = -1)
lm_logits = модель (Нет, encoder_outputs = encoded_sequence, decoder_input_ids = decoder_input_ids, return_dict = True).логиты
next_decoder_input_ids = torch.argmax (lm_logits [:, -1:], ось = -1)
decoder_input_ids = torch.cat ([decoder_input_ids, next_decoder_input_ids], axis = -1)
lm_logits = модель (Нет, encoder_outputs = encoded_sequence, decoder_input_ids = decoder_input_ids, return_dict = True) .logits
next_decoder_input_ids = torch.argmax (lm_logits [:, -1:], ось = -1)
decoder_input_ids = torch.cat ([decoder_input_ids, next_decoder_input_ids], axis = -1)
print (f "Создано на данный момент: {tokenizer.decode (decoder_input_ids [0], skip_special_tokens = True)}")
Выходы:
Сгенерировано пока: Ich Ich
В этом примере кода мы показываем именно то, что было описано ранее.Мы
передайте ввод "Я хочу купить машину" вместе с BOS \ text {BOS} BOS
токен модели кодера-декодера и выборка из первого логита l1 \ mathbf {l} _1l1 (, т.е. первая строка lm_logits ). Настоящим наша выборка
стратегия проста - жадно выбрать следующий входной вектор декодера, который
имеет наибольшую вероятность. Затем авторегрессивным образом мы передаем
выбранный входной вектор декодера вместе с предыдущими входами для
модель кодировщика-декодера и снова образец.Повторяем это в третий раз.
В результате модель сформировала слова «Ич Ич». Первое
слово точное! Второе слово не очень хорошее. Мы можем видеть здесь,
что хороший метод декодирования является ключом к успешной генерации последовательности
из заданного модельного распределения.
На практике используются более сложные методы декодирования для выборки lm_logits . Большинство из них покрыто
это сообщение в блоге.
Понимание шумихи вокруг моделей Transformer NLP
Чтобы понять шумиху вокруг моделей Transformer NLP и их практическое значение, стоит сделать шаг назад и изучить архитектуру и внутреннюю работу этих моделей.В этом сообщении блога мы расскажем вам о возникновении архитектуры Transformer NLP, начиная с ее ключевого компонента - парадигмы внимания.
История возникновения механизмов внимания: машинный перевод
Парадигма внимания вошла в сферу НЛП еще в 2014 году, до ажиотажа в области глубокого обучения, и впервые была применена к проблеме машинного перевода.
Обычно система машинного перевода следует базовой архитектуре кодер-декодер (как показано на изображении ниже), где и кодер, и декодер, как правило, являются вариантами рекуррентных нейронных сетей (RNN).Чтобы понять, как работает RNN, полезно представить ее как последовательность ячеек. Кодировщик RNN получает входное предложение и считывает его по одному токену за раз: каждая ячейка получает входное слово и создает скрытое состояние в качестве выходных данных, которое затем подается в качестве входных данных в следующую ячейку RNN, пока все слова в предложении не будут обработанный.
После этого последнее сгенерированное скрытое состояние, мы надеемся, уловит суть всей информации, содержащейся в каждом слове входного предложения.Этот вектор, называемый вектором контекста, затем будет передан в качестве входных данных в декодер RNN, который будет производить переведенное предложение по одному слову за раз.
Но можно ли разумно предположить, что вектор контекста может сохранять ВСЮ необходимую информацию входного предложения? А что, если предложение состоит, скажем, из 50 слов? Из-за присущей RNN последовательной структуры каждая входная ячейка создает только один выходной вектор скрытого состояния для каждого слова в предложении, один за другим. Из-за последовательного порядка обработки текста контекстному вектору сложнее захватить всю информацию, содержащуюся в предложении, для длинных предложений со сложными зависимостями между словами - это называется «проблемой узкого места».
Устранение проблемы узких мест с вниманием
Чтобы решить эту проблему узкого места, исследователи создали метод, обращающий внимание на конкретные слова. При переводе предложения или расшифровке аудиозаписи агент-человек обращает особое внимание на слово, которое он в настоящее время переводит или расшифровывает.
Нейронные сети могут достичь того же поведения, используя внимание, сосредотачиваясь на части подмножества предоставляемой информации.Помните, что каждая входная ячейка RNN создает один скрытый вектор состояния для каждого входного слова. Затем мы можем объединить эти векторы, усреднить их или (что еще лучше!) Взвесить их, чтобы придать большее значение словам из входного предложения, которые наиболее важны для декодирования следующего слова (выходного предложения). В этом вся суть техники внимания.
Если вы хотите еще больше разобраться в деталях моделей Transformer NLP и внутренней работе механизма внимания, мы рекомендуем вам прочитать этот пост в блоге Data From the Trenches .
На пути к моделям трансформатора NLP
Как вы теперь понимаете, внимание было революционной идеей в системах последовательного перевода, таких как модели перевода. Модели Transformer NLP основаны на механизме Attention, который развивает его основную идею еще дальше: в дополнение к использованию Attention для вычисления представлений (то есть векторов контекста) из векторов скрытого состояния кодировщика, почему бы не использовать Attention для вычисления векторов скрытых состояний кодировщика самих себя? Непосредственным преимуществом этого является избавление от неотъемлемой последовательной структуры RNN, которая препятствует распараллеливанию моделей.
Чтобы решить проблему распараллеливания, Attention увеличивает скорость преобразования модели из одной последовательности в другую. Таким образом, основным преимуществом моделей Transformer NLP является то, что они не являются последовательными, что означает, что, в отличие от RNN, их легче распараллелить, и что все большие и большие модели можно обучать путем распараллеливания обучения.
Более того, модели Transformer NLP пока демонстрируют лучшую производительность и скорость, чем модели RNN.Из-за всех этих факторов большая часть исследований НЛП за последние пару лет была сосредоточена на моделях Трансформаторного НЛП, и мы можем ожидать, что это приведет к появлению новых интересных бизнес-сценариев.
Декодирование AI и NLP для издателей
В сегодняшних цифровых издательских кругах - когда у вас есть такие термины, как: искусственный интеллект (AI) и обработка естественного языка (NLP), которые так часто используются, вам будет полезно познакомиться с ними и, по сути, изучить их. в режиме реального времени для потенциальных вариантов использования в издательском пространстве.
Благодаря сложным рабочим процессам, характеризующим большую часть издательской экосистемы, возможности ИИ являются весьма многообещающими в той степени, в которой они могут фактически автоматизировать значительную часть этих рабочих процессов и создать значительную ценность для издательского бизнеса, авторов и исследовательского сообщества.
В этом блоге давайте расскажем, как ИИ и НЛП приносят пользу в издательском пространстве.
Расширение возможностей редакторов в принятии решений
AI расширяет возможности человека, помогая машинам определять и создавать новые модели.Он включает в себя разработку алгоритмов, которые позволяют машинам быстро обрабатывать большие объемы данных, распознавать согласованные закономерности в этих данных, принимать решения, основанные на понимании, и предоставлять рекомендации на основе этого анализа. По сути, ИИ может максимально упростить процесс публикации.
Исправление мелких ошибок
Благодаря встроенным технологиям искусственного интеллекта и НЛП инструменты цифрового редактирования могут анализировать каждую попавшуюся статью с помощью предварительно установленных правил грамматики и форматирования.После анализа содержания технология помогает оценить, является ли статья хорошим и пригодным для публикации. Технология автоматически исправляет мелкие ошибки, такие как грамматические и пунктуационные, и помечает более сложные проблемы, которые могут потребовать внимания редактора. Представленные журналы качественные и позволяют сразу перейти к этапу набора и составления.
Автоматизация рабочих процессов
AI может интеллектуально автоматизировать рабочие процессы, чтобы сократить время публикации, улучшить редакционное качество, повысить удобство работы авторов и повысить оперативность научных исследований.Искусственный интеллект и НЛП могут быть использованы для создания сенсации в процессе рецензирования путем оценки рукописей, извлечения ключевых терминов для определения оригинальности и сопоставления взаимосвязей, проверки качества языка, выявления плагиата и даже сопоставления статей с журналами и рецензентами.
Ускорение внутренних производственных процессов и сокращение времени выполнения заказа
Поскольку производственные процессы отнимают очень много времени и существует постоянный спрос на более быстрые, дешевые и короткие сроки выполнения работ, ИИ может увеличить скорость процесса редактирования и лучше обслуживать авторов, обеспечивая более своевременную публикацию.ИИ / НЛП стали незаменимыми, начиная с просеивания большого объема входящего контента и заканчивая пометкой контента и аномалиями процессов.
NLP включает грамматический анализ в машинное обучение. Компьютерная программа обучается распознавать существительное, глагол и объект в предложении, а также понимать структуру слов, чтобы различать их значение. С помощью технологии NLP издатели могут автоматизировать простые задачи редактирования и форматирования и сосредоточиться на более сложных задачах.
Сокращение длительных циклов проверки
За счет уменьшения количества точек соприкосновения, через которые должен проходить документ, ИИ и НЛП вместе могут увеличить скорость прохождения через систему, используя алгоритмы, вместо того, чтобы ждать циклов ручного просмотра, которые обычно длительны и отнимают много времени.Это сокращает ручное редакционное вмешательство и, возможно, даже может уменьшить элемент человеческой предвзятости.
Итак, каков последний результат?
Есть два способа увидеть преимущества, которые AI / NLP может принести издательскому столу. С одной стороны, их можно использовать для оптимизации рабочих процессов публикации и, таким образом, для улучшения опыта авторов, поскольку решения, основанные на данных, всегда берут верх над выводами из первых рук. С другой стороны, издатели рассматривают ИИ и НЛП как полезные технологические инструменты, которые могут резко снизить затраты и повысить эффективность работы, одновременно улучшая эффективность рабочего процесса публикации и качество продукции.
API декодирования | Текст | TensorFlow
Обзор
В недавнем прошлом было проведено много исследований в области генерации языков с помощью авторегрессивных моделей. В авторегрессивной языковой генерации распределение вероятностей токена на временном этапе K зависит от предсказаний токенов модели до этапа K-1 . Для этих моделей стратегии декодирования, такие как поиск луча, жадный, Top-p и Top-k, являются критическими компонентами модели и в значительной степени влияют на стиль / характер сгенерированного выходного токена на заданном временном шаге K .
Например, Поиск луча снижает риск пропуска скрытых токенов высокой вероятности на сохранение наиболее вероятного числа гипотез на каждом временном шаге и, в конечном итоге, выбор гипотезы с наибольшей общей вероятностью. Мюррей и др. (2018) и Ян и др. (2018) показывают, что поиск луча хорошо работает в задачах машинного перевода. Обе стратегии Beam search и Greedy могут генерировать повторяющиеся токены.
Fan et.al (2018) представил Top-K выборка , в которой K наиболее вероятных токенов отфильтрованы, а масса вероятности перераспределяется только между этими токенами K.
Ari Holtzman et. al (2019) представил Выборка Top-p , которая выбирает из наименьшего возможного набора токенов с совокупная вероятность, которая складывается с вероятностью p . Тогда вероятностная масса равна распространяется среди этого набора. Таким образом, размер набора токенов может динамически увеличиваются и уменьшаются. Top-p, Top-k обычно используются в таких задачах, как создание историй.
Decoding API предоставляет интерфейс для экспериментов с различными стратегиями декодирования на авторегрессионных моделях.
Следующие стратегии выборки представлены в sampling_module.py, который наследуется от базового класса Decoding:
Поиск луча предоставляется в файле beam_search.py. гитхаб
Установка
pip install -q -U tenorflow-text
pip install -q tf-models-nightly
импортировать numpy как np
import matplotlib.pyplot как plt
импортировать тензорный поток как tf
из официального импорта nlp
from official.nlp.modeling.ops import sampling_module
from official.nlp.modeling.ops import beam_search
Инициализировать модуль выборки в TF-NLP.
- symbols_to_logits_fn : Используйте это замыкание, чтобы вызвать модель для прогнозирования логитов для шага
index + 1. Входы и выходы для этого закрытия следующие:
Аргументы:
1] ids: Текущие декодированные последовательности.int тензор с формой (batch_size, index + 1 или 1, если padded_decode имеет значение True)],
2] index [скаляр]: текущий шаг декодирования,
3] cache [вложенный словарь тензоров]: используется только для более быстрого декодирования для хранения предварительно вычисленных скрытых состояний для ключей и значений. Больше объяснений в ячейке ниже.
Возврат:
1] тензор для логитов следующего шага [batch_size, vocab]
2] updated_cache [вложенный словарь тензоров].
Кэш используется для более быстрого декодирования. Вот эталонная реализация вышеуказанного закрытия.
- length_normalization_fn : Используйте это замыкание для возврата параметра нормализации длины.
Аргументы:
1] length: скаляр для индекса декодированного шага.
2] dtype: тип данных выходного тензора
Возврат:
1] значение коэффициента нормализации длины.
vocab_size : Размер выходного словаря.
max_decode_length : Скаляр для общего количества шагов декодирования.
eos_id : Декодирование остановится, если все выходные декодированные идентификаторы в пакете имеют этот eos_id.
padded_decode : Установите значение True, если работает на TPU. Тензоры дополняются до max_decoding_length, если это True.
top_k : top_k включен, если это значение> 1.
top_p : top_p включен, если это значение> 0 и <1.0
sampling_temperature : Используется для повторной оценки выхода softmax. Температура искажает распределение в сторону жетонов с высокой вероятностью и снижает массу в распределении хвостов.Значение должно быть положительным. Низкая температура эквивалентна жадности и делает распределение более резким, а высокая температура делает его более плоским.
enable_greedy : по умолчанию это True и жадное декодирование включено. Чтобы поэкспериментировать с другими стратегиями, установите значение False.
Инициализировать гиперпараметры модели
params = {}
params ['num_heads'] = 2
params ['num_layers'] = 2
params ['batch_size'] = 2
params ['n_dims'] = 256
params ['max_decode_length'] = 4
В авторегрессивных архитектурах, таких как модели кодировщика-декодера на базе трансформатора, Кэш используется для быстрого последовательного декодирования.Это вложенный словарь, хранящий предварительно вычисленные скрытые состояния (ключ и значения в блоках самовнимания и в блоках перекрестного внимания) для каждого слоя.
Инициализировать кеш.
cache = {
'layer_% d'% layer: {
'k': tf.zeros ([params ['batch_size'], params ['max_decode_length'], params ['num_heads'], int (params ['n_dims'] / params ['num_heads'])], dtype = tf.float32),
'v': tf.zeros ([params ['batch_size'], params ['max_decode_length'], params ['num_heads'], int (params ['n_dims'] / params ['num_heads'])], dtype = тф.float32)
} для слоя в диапазоне (params ['num_layers'])
}
print ("форма ключа кеширования для слоя 1:", cache ['layer_1'] ['k']. shape)
форма ключа кэша для слоя 1 & двоеточие; (2, 4, 2, 128) 2021-08-11 18 & двоеточие; 44 & двоеточие; 59.884533 & двоеточие; I tensorflow / stream_executor / cuda / cuda_gpu_executor.cc & двоеточие; 939] успешное чтение узла NUMA из SysFS имело отрицательное значение (-1), но должен быть хотя бы один узел NUMA, поэтому узел NUMA возвращается ноль 2021-08-11 18 & двоеточие; 44 & двоеточие; 59.892742 & двоеточие; I tensorflow / stream_executor / cuda / cuda_gpu_executor.cc & двоеточие; 939] успешное чтение узла NUMA из SysFS имело отрицательное значение (-1), но должен быть хотя бы один узел NUMA, поэтому узел NUMA возвращается ноль 2021-08-11 18 & двоеточие; 44 & двоеточие; 59.893649 & двоеточие; I tensorflow / stream_executor / cuda / cuda_gpu_executor.cc & двоеточие; 939] успешное чтение узла NUMA из SysFS имело отрицательное значение (-1), но должен быть хотя бы один узел NUMA, поэтому узел NUMA возвращается ноль 2021-08-11 18 & двоеточие; 44 & двоеточие; 59.895413 & двоеточие; I tenorflow / core / platform / cpu_feature_guard.cc & col; 151] Этот двоичный файл TensorFlow оптимизирован с помощью библиотеки глубокой нейронной сети oneAPI (oneDNN) для использования следующих инструкций ЦП в критических для производительности операциях & двоеточие; AVX2 AVX512F FMA Чтобы включить их в других операциях, перестройте TensorFlow с соответствующими флагами компилятора. 2021-08-11 18 & двоеточие; 44 & двоеточие; 59.896128 & двоеточие; I tensorflow / stream_executor / cuda / cuda_gpu_executor.cc & двоеточие; 939] успешное чтение узла NUMA из SysFS имело отрицательное значение (-1), но должен быть хотя бы один узел NUMA, поэтому узел NUMA возвращается ноль 2021-08-11 18 & двоеточие; 44 & двоеточие; 59.897135 & двоеточие; I tensorflow / stream_executor / cuda / cuda_gpu_executor.cc & двоеточие; 939] успешное чтение узла NUMA из SysFS имело отрицательное значение (-1), но должен быть хотя бы один узел NUMA, поэтому узел NUMA возвращается ноль 2021-08-11 18 & двоеточие; 44 & двоеточие; 59.898014 & двоеточие; I tensorflow / stream_executor / cuda / cuda_gpu_executor.cc & двоеточие; 939] успешное чтение узла NUMA из SysFS имело отрицательное значение (-1), но должен быть хотя бы один узел NUMA, поэтому узел NUMA возвращается ноль 2021-08-11 18 & двоеточие; 45 & двоеточие; 00.440341 & двоеточие; I tensorflow / stream_executor / cuda / cuda_gpu_executor.cc & двоеточие; 939] успешное чтение узла NUMA из SysFS имело отрицательное значение (-1), но должен быть хотя бы один узел NUMA, поэтому узел NUMA возвращается ноль 2021-08-11 18 & двоеточие; 45 & двоеточие; 00.441305 & двоеточие; I tensorflow / stream_executor / cuda / cuda_gpu_executor.cc & двоеточие; 939] успешное чтение узла NUMA из SysFS имело отрицательное значение (-1), но должен быть хотя бы один узел NUMA, поэтому узел NUMA возвращается ноль 2021-08-11 18 & двоеточие; 45 & двоеточие; 00.442196 & двоеточие; I tensorflow / stream_executor / cuda / cuda_gpu_executor.cc & двоеточие; 939] успешное чтение узла NUMA из SysFS имело отрицательное значение (-1), но должен быть хотя бы один узел NUMA, поэтому узел NUMA возвращается ноль 2021-08-11 18 & двоеточие; 45 & двоеточие; 00.443081 & двоеточие; I tensorflow / core / common_runtime / gpu / gpu_device.cc & col; 1505] Создано устройство / задание & двоеточие; localhost / replica & двоеточие; 0 / задача & двоеточие; 0 / устройство & двоеточие; GPU & двоеточие; 0 с памятью 14662 МБ и двоеточием; -> устройство и двоеточие; 0, имя & двоеточие; Tesla V100-SXM2-16GB, идентификатор шины pci и двоеточие; 0000 & двоеточие; 00 & двоеточие; 05.0, вычислительные возможности и двоеточие; 7.0
Определите замыкание для нормализации длины, если необходимо.
Используется для нормализации окончательных оценок сгенерированных последовательностей и является необязательным.
def length_norm (длина, dtype):
"" "Коэффициент нормализации длины возврата." ""
return tf.pow (((5. + tf.cast (длина, dtype)) / 6.), 0.0)
Создать model_fn
На практике это будет заменено реальной реализацией модели, такой как здесь
Аргументы:
i: Шаг, который декодируется.Возврат:
логит вероятности размера [batch_size, 1, vocab_size]
вероятностей = tf.constant ([[[0,3, 0,4, 0,3], [0,3, 0,3, 0,4],
[0,1, 0,1, 0,8], [0,1, 0,1, 0,8]],
[[0,2, 0,5, 0,3], [0,2, 0,7, 0,1],
[0,1, 0,1, 0,8], [0,1, 0,1, 0,8]]])
def model_fn (i):
вероятности возврата [:, i,:]
Инициализировать символы_to_logits_fn
def _symbols_to_logits_fn ():
"" "Вычисляет логиты следующих токенов."" "
def symbols_to_logits_fn (ids, i, temp_cache):
del ids
logits = tf.cast (tf.math.log (model_fn (i)), tf.float32)
вернуть логиты, temp_cache
вернуть символы_to_logits_fn
Жадный
Жадное декодирование выбирает идентификатор токена с наибольшей вероятностью в качестве его следующего идентификатора: $ id_t = argmax_ {w} P (id | id_ {1: t-1}) $ на каждом временном шаге $ t $. На следующем рисунке показано жадное декодирование.
greedy_obj = sampling_module.SamplingModule (
length_normalization_fn = Нет,
dtype = tf.float32,
символы_to_logits_fn = _symbols_to_logits_fn (),
voiceab_size = 3,
max_decode_length = params ['max_decode_length'],
eos_id = 10,
padded_decode = Ложь)
ids, _ = greedy_obj.generate (
initial_ids = tf.constant ([9, 1]), initial_cache = кеш)
print ("Жадно декодированные идентификаторы:", идентификаторы)
Жадно декодированные идентификаторы и двоеточие; tf.Tensor ( [[9 1 2 2 2] [1 1 1 2 2]], shape = (2, 5), dtype = int32)
top_k выборка
В выборке Top-K , K наиболее вероятных идентификаторов следующих токенов фильтруются, и масса вероятности перераспределяется только между этими K идентификаторами.
top_k_obj = sampling_module.SamplingModule (
length_normalization_fn = длина_норма,
dtype = tf.float32,
символы_to_logits_fn = _symbols_to_logits_fn (),
voiceab_size = 3,
max_decode_length = params ['max_decode_length'],
eos_id = 10,
sample_temperature = tf.constant (1.0),
top_k = tf.constant (3),
padded_decode = Ложь,
enable_greedy = Ложь)
ids, _ = top_k_obj.generate (
initial_ids = tf.constant ([9, 1]), initial_cache = кеш)
print ("топ-k выборочных идентификаторов:", ids)
ИД и двоеточие, выбранные для выборки топ-k; tf.Тензор( [[9 1 2 2 2] [1 2 1 2 2]], shape = (2, 5), dtype = int32)
top_p выборка
Вместо выборки только из наиболее вероятных K идентификаторов токенов, в Top-p выборка выбирает из наименьшего возможного набора идентификаторов, совокупная вероятность которых превышает вероятность p .
top_p_obj = sampling_module.SamplingModule (
length_normalization_fn = длина_норма,
dtype = tf.float32,
символы_to_logits_fn = _symbols_to_logits_fn (),
voiceab_size = 3,
max_decode_length = params ['max_decode_length'],
eos_id = 10,
sample_temperature = tf.константа (1.0),
top_p = tf.constant (0.9),
padded_decode = Ложь,
enable_greedy = Ложь)
ids, _ = top_p_obj.generate (
initial_ids = tf.constant ([9, 1]), initial_cache = кеш)
print ("ID выборки top-p:", ids)
идентификаторы выборки top-p и двоеточие; tf.Tensor ( [[9 0 1 1 2] [1 0 1 2 2]], shape = (2, 5), dtype = int32)
Расшифровка поиска луча
Поиск луча снижает риск пропуска скрытых идентификаторов токенов высокой вероятности, сохраняя наиболее вероятное число гипотез на каждом временном шаге и, в конечном итоге, выбирая гипотезу, которая имеет наибольшую общую вероятность.
beam_size = 2
params ['batch_size'] = 1
beam_cache = {
'layer_% d'% layer: {
'k': tf.zeros ([params ['batch_size'], params ['max_decode_length'], params ['num_heads'], params ['n_dims']], dtype = tf.float32),
'v': tf.zeros ([params ['batch_size'], params ['max_decode_length'], params ['num_heads'], params ['n_dims']], dtype = tf.float32)
} для слоя в диапазоне (params ['num_layers'])
}
print ("форма ключа кэша для слоя 1:", beam_cache ['layer_1'] ['k']. shape)
идентификаторы, _ = beam_search.sequence_beam_search (
символы_to_logits_fn = _symbols_to_logits_fn (),
initial_ids = tf.constant ([9], tf.int32),
initial_cache = кэш-лучей,
voiceab_size = 3,
beam_size = beam_size,
альфа = 0,6,
max_decode_length = params ['max_decode_length'],
eos_id = 10,
padded_decode = Ложь,
dtype = tf.float32)
print ("Идентификаторы поиска луча:", идентификаторы)
форма ключа кэша для слоя 1 & двоеточие; (1, 4, 2, 256) Идентификаторы поиска луча и двоеточие; tf.Tensor ( [[[9 0 1 2 2] [9 1 2 2 2]]], shape = (1, 2, 5), dtype = int32)
Расшифровка ДНК потока данных с помощью NLP
Автор: Сатьякам Моханти , руководитель подразделения Leni and Mosaic Applied Intelligence, LTI
Мы обсудили, как Генератор естественного языка (NLG) ускоряет весь путь от данных к решению в моем предыдущем блоге.Давайте рассмотрим обработку естественного языка (НЛП) и то, как она играет ключевую роль во взаимодействии между людьми и компьютерами на естественном языке.
Записанный беспредел
Вы не поверите, но каждый день генерируется 2,5 квинтиллиона байтов данных. Основным источником этого океана данных является фармацевтическая промышленность и здравоохранение, благодаря тому, что медицинские записи оцифровываются каждую секунду. Эти данные собираются из личных фитнес-трекеров, медицинских интеллектуальных устройств, из новых исследований, правительственных отчетов и медицинских записей, которые создаются каждый день.
Благодаря аналитике больших данных и искусственному интеллекту современные и завтрашние медицинские данные могут влиять на процесс принятия решений и трансформировать его. Но на этом пути возникают проблемы, одна из которых - данные, хранящиеся в различных неструктурированных форматах. К ним относятся электронные медицинские карты, записи врача, показания носимых устройств, исследования и т. Д., Которые могут быть несовместимы друг с другом. Эта универсальность данных является большим препятствием, когда дело доходит до внедрения больших данных из-за их размера и сложности.
NLP приходит на помощь
Фармацевтическая промышленность наводнена неструктурированными данными. НЛП может облегчить извлечение данных из разных форматов, источников и языков в общий. НЛП отлично работает в этих сценариях, потому что способствует беспрепятственному взаимодействию между компьютером и людьми с использованием естественного языка.
Вот как NLP может помочь максимально использовать медицинские данные:
Медицинская документация
Практикующие врачи записывают огромные объемы данных.Алгоритмы НЛП позволяют медицинскому персоналу записывать и хранить общие заметки и наблюдения в стандартных форматах, которые можно легко обрабатывать. Это также может помочь им принести большую пользу пациентам за счет создания автоматизированных и настраиваемых наборов учебных материалов и руководств во время выписки.
Автоматизация обработки медицинских записей
Больницы могут запускать алгоритмы обработки естественного языка для неструктурированных данных в электронных медицинских записях (EMR).Этот процесс будет автоматически извлекать особенности или факторы риска из заметок, а также автоматически сохранять медицинские записи.
Выявление факторов риска
Неструктурированные данные пациента могут предоставить кладезь информации и дать глубокое понимание состояния пациента. Мол, у пациента депрессия? Каковы бытовые условия больного? Они бездомные? Такие важные данные похоронены в неструктурированных форматах данных. Это может помочь поставщикам медицинских услуг выявлять и выявлять пациентов с повышенным фактором риска и предлагать им целевые программы лечения.
Повышение уровня санитарной грамотности пациентов
ИТ-инструменты на основе НЛП могут помочь в обработке электронных медицинских карт и интеграции результатов в упрощенные форматы для непрофессионала. Этой информацией можно поделиться с пациентами через портал для лучшего понимания их болезни.
Таким образом, НЛП в сочетании с ИИ и машинным обучением может стать настоящей находкой для фармацевтических компаний. Это может помочь им выйти за рамки поверхностного понимания, получить практические идеи и ускорить внедрение инноваций, чтобы оставаться впереди конкурентов.
Интеллектуальные решения
В этой увлекательной серии блогов я раскрываю различные аспекты роли ИИ и аналитики в медико-биологической и фармацевтической промышленности.
Другие темы, затронутые в серии :
Серия AI Remedy: рецепты для интеллектуальных преобразований
Серия AI Remedy: реформирование отрасли с помощью искусственного интеллекта
Серия AI Remedy: NLG - ускорение пути от данных до принятия решений
 Оно отсылает нас к языковым моделям, играющим важную роль в достижении взаимопонимания между людьми, на чем, собственно, и держатся все коммуникационные процессы. В самом деле, трудно представить себе сознательное мышление вне связи с языком – как часто мы говорим сами с собой, даем себе советы, ругаем себя за что–то.
Оно отсылает нас к языковым моделям, играющим важную роль в достижении взаимопонимания между людьми, на чем, собственно, и держатся все коммуникационные процессы. В самом деле, трудно представить себе сознательное мышление вне связи с языком – как часто мы говорим сами с собой, даем себе советы, ругаем себя за что–то.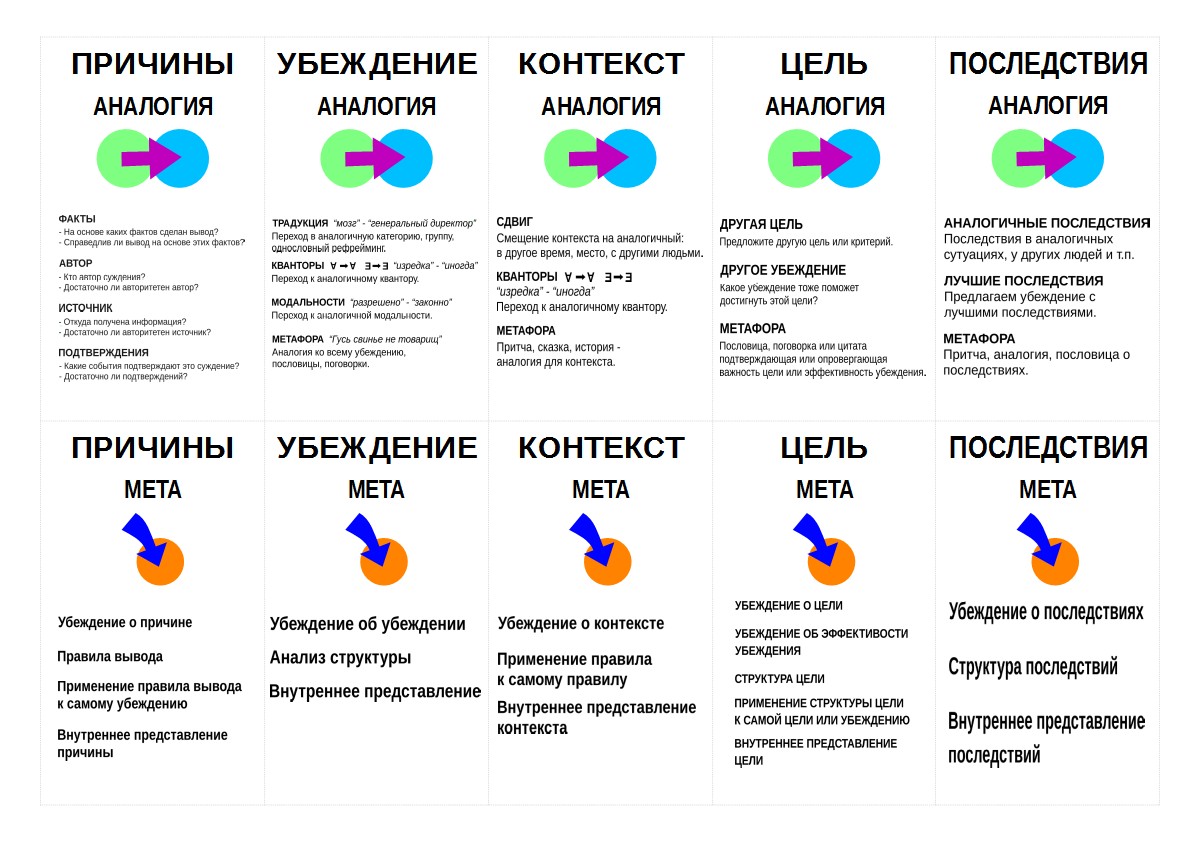 Во-вторых, «сознание» обрабатывает информацию посредством вторичной языковой системы символов, слов,метафор и т. д.
Во-вторых, «сознание» обрабатывает информацию посредством вторичной языковой системы символов, слов,метафор и т. д.