Формы мышления. 11-й класс

Цель: ввести основные понятия формальной логики.

(Приложение 1.)

Слайд 1.

Сегодня мы приступаем к изучению новой раздела математической науки под названием Логика. Прослушав мое вступление, запишите, для чего нужно изучать логику.
Познание истины – одна из важнейших потребностей человека. Каждый человек и человечество в целом стремятся к истине, добру и красоте. Все люди нуждаются в истинном знании, получении новой информации о мире, в котором они живут. Для чего? Для того чтобы жить, что в данном случае означает ориентироваться в быстро меняющейся обстановке, принимать правильные решения и на их основе совершать правильные действия.

Слайд 2.

Представьте себе круг вашего знания по логике сегодня, только в начале ее изучения. Это знание невелико, и его можно изобразить небольшим кружочком. Вне этого кружочка лежит все то, чего вы пока не знаете.

Его граница является границей вашего знания, но одновременно она является и границей вашего незнания.
Сократ знал, конечно же, гораздо больше в этой области знаний, чем вы сейчас, потому что много размышлял и не боялся высказывать то, о чем он думал.
Круг его знания изобразим в виде большого круга.
Заметим, что граница его незнания существенно больше границы вашего. Теперь вам понятно, почему он воскликнул: “Я знаю, что ничего не знаю!”?
Человек с древних времен стремился познать законы правильного мышления, т.е. логические законы. Наука логика помогает познанию этих законов.

Законы развития есть у природы, общества, любой сложной системы и, конечно же, у самого мышления. Существует даже мнение, что всякое движение нашей мысли, постигающей истину, добро и красоту, опирается на логические законы. Мы можем их не осознавать, но вынуждены всегда следовать этим законам, чтобы жить в обществе, общаться с людьми, понимать их и быть понятыми.
В Древней Греции, Древней Индии, Древнем Риме законы и формы правильного мышления изучались в рамках ораторского искусства. Применение логических приемов рассуждения позволяло ораторам более убедительно доносить до аудитории их точку зрения, склонять людей на свою сторону.
Мыслить логично – значит мыслить точно и последовательно, не допуская противоречий в своих рассуждениях, уметь вскрывать логические ошибки.
Представьте себе, что вас спросили: “Почему днем бывает светло?” А вы ответили: “Потому что днем свет делает день светлым”. Вы нарушили правила логики и, по сути, ничего не объяснили.

Слайд 3.

Логика – одна из древнейших наук. Ее основателем считается величайший древнегреческий философ Аристотель, который первым систематизировал формы и правила мышления, обстоятельно исследовал категории “понятие” и “суждение”, подробно разработал теорию умозаключений и доказательств, описал ряд логических операций, сформулировал основные законы мышления.

Слайд 4.

Для чего же изучают логику?
Итак, предметом исследования науки логики является человеческое мышление. Мышление всегда существует в каких-то формах. В логике выделяют следующие формы мышления: понятие, суждение, умозаключение.
Рассмотрим эти формы мышления.

Слайд 5.

Понятие – форма мышления, отражающая основные, существенные признаки предмета.

Примеры понятий:

• Апельсин
• Трапеция
• Белизна
• река Нил
• ураганный ветер
• студент медицинского института

Например, признаками понятия апельсин являются: круглый, оранжевый, сладкий, ароматный. Можно ли по этим признакам отличить апельсин о неапельсина?

Слайд 6.

В 18 веке Леонард Эйлер предложил способ наглядной геометрической иллюстрации объемов понятий и отношений между ними, которая носит название кругов Эйлера.
Рассмотрим множество учеников вашего класса (Е). Те ученики, которые занимаются спортом, образуют множество спортсменов (А). Те, кто увлекается литературой, образуют множество (В). Те, кто учится на одни пятерки и четверки и на каникулах отдыхает у бабушки, образуют еще одно множество (С). Предположим, что среди учеников, составляющих множество С, нет ни одного, занимающегося спортом, т.е. множества С и А не имеют общих элементов. Множество учеников класса, которые знают пять иностранных языков (D), будет пустым, если таких полиглотов в вашем классе нет. Данную ситуацию графически можно изобразить, например, так.

Слайд 7.

Суждение (высказывание, утверждение) – форма мышления, в которой что-либо утверждается или отрицается о предметах, их свойствах или отношениях между ними.

Примеры суждений:

• этот апельсин вкусный.
• Если прошел дождь, то на улице весна.
• На Луне живут лунатики, а на Марсе – марсиане.

Слайд 8.

Языковым выражением суждений являются повествовательные предложения. Суждение бывает простым и сложным.

• Наступила весна.
• Наступила весна, и прилетели грачи.

Всякое суждение может быть либо истинным, либо ложным. Одно и то же суждение разными людьми может восприниматься как истинное или ложное в зависимости от их взглядов, жизненного опыта, особенностей национальной культуры, воспитания, образования и т.д.

Например, для кого-то истинным является, что свободу, безопасность и комфорт дают глубокие знания, а для кого-то – свободу, безопасность и комфорт дают большие деньги.
Для того чтобы вести рассуждения и оценивать их правильность, необходимо прежде договориться по каждому суждению, будем ли мы его рассматривать как истинное или ложное в каждом конкретном случае. Например, суждение – Он хороший шахматист может быть как истинным, так и ложным, в зависимости от того, кто имеется в виду под местоимением “он”. Заметим, что “договориться” мы можем только по отношению к простым суждениям. Значения же истинности сложных суждений вычисляется. При вычислении истинности (ложности) сложного суждения содержание входящих в него простых суждений является незначимым. Интерес представляет то, чем суждения отличаются друг от друга, что характеризует каждое из них, а именно их форма.

Слайд 9.

Форма суждения, в отличие от его содержания, объективна, т.е. не зависит от тех или иных взглядов того или иного человека.

Попробуйте определить логическую форму следующих суждений:

• Все лошади едят овес
• Все реки впадают в море
• Все школьники – отличники
• Все книги имеют страницы
• Все планеты вращаются вокруг звезд

Во всех этих рассуждениях говорится о разном, но они имеют одинаковую логическую форму: Все S есть Р.

А суждения

• Все медузы не имеют головы
• Люди не боги

имеют другую логическую форму: Все S не есть Р.

Слайд 10.

Умозаключение – форма мышления, с помощью которой из одного или нескольких суждений получают новое суждение.
В русском языке слово “умозаключение” используется в двух значениях: для обозначения процесса рассуждения, размышления, приводящего к некоторому выводу, и для обозначения результата этого процесса.

Слайд 11.

Еще в древности было известно рассуждение, ставшее классическим образцом верного логического умозаключения:

• Все люди смертны.
• Сократ – человек.
• Сократ смертен.

Заметим, что посылками умозаключения по правилам логики могут быть только истинные суждения. Всякое умозаключение, так же как и суждение, имеет свою форму. Эта форма может быть логически правильной или логически неправильной. Так, в примере с Сократом, форма умозаключения логически верная.

Слайд 12.

Примеры верных умозаключений:

1) Четырехугольник, у которого противоположные стороны параллельны, есть параллелограмм.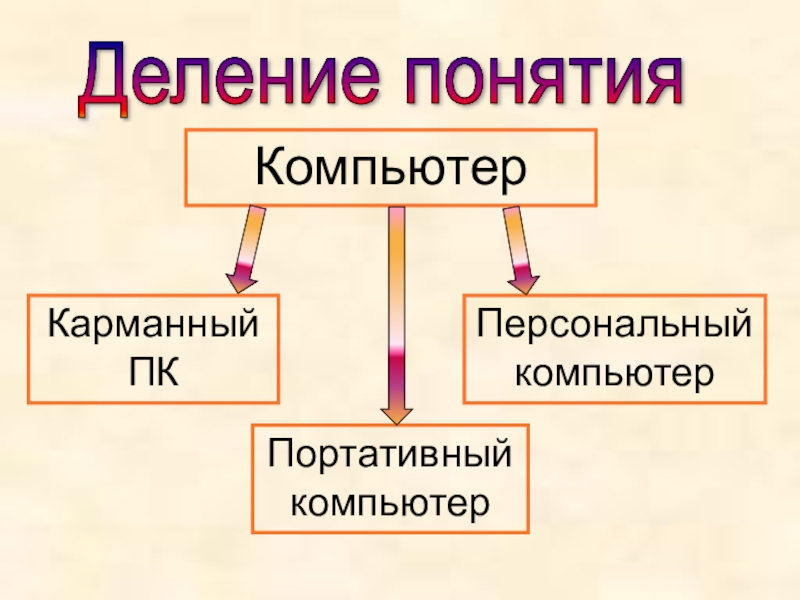
Квадрат – это четырехугольник, у которого противоположные стороны параллельны.
Квадрат – это параллелограмм.

2) Все граждане России имеют право на отдых.
Я – гражданин России.
Я имею право на отдых.

Слайд 13.

3) Если цветы поливают, то они не засохнут.
Цветы засохли.
Цветы не поливали.

Слайд 14.

Правильно ли рассуждает человек, когда он говорит:

Если что-то есть металл, то оно проводит электрический ток.
Алюминий проводит ток.
Алюминий – металл.

Из истинных посылок получилось истинное заключение. Можно предположить, что, рассуждая по данной форме, мы получим из истинных посылок истинное заключение во всех случаях. Проверим это:

Если что-то есть металл, то оно проводит электрический ток.
Вода проводит ток.
Вода – металл.

Из истинных посылок получилось ложное заключение. Наше предположение о том, что, рассуждая по данной форме, мы всегда из истинных посылок получим истинное заключение, ошибочно.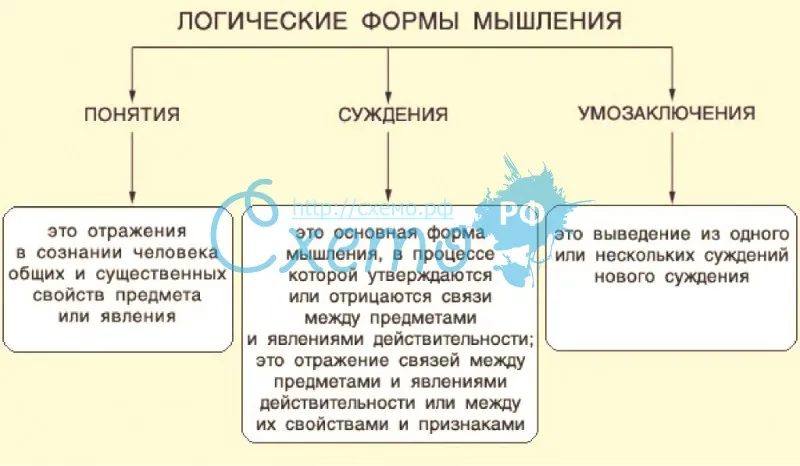 Следовательно, те, кто рассуждает по данной форме, либо ошибаются сами, либо вводят слушателей в заблуждение.

Определите истинность или ложность следующих умозаключений:

1) Если у человека повышена температура, то он болен; этот человек болен; следовательно, у него должна быть повышенная температура.
2) Все зебры полосаты; это животное полосато; это животное зебра
3) Бутылки с ряженкой продаются в молочном отделе. Эта бутылка куплена в молочном отделе. Это бутылка с ряженкой.
4) Все школьники – отличники. Вовочка – школьник. Вовочка – отличник.
5) Людей много. Сократ человек. Сократов много.

Вывод: итак, с точки зрения содержания суждений в процессе мышления формируется истинное или ложное отражение мира, а если рассматривать мышление со стороны формы, то имеет значение только его логическая правильность или неправильность.

Слайд 15.

ДЗ.

1. Приведите по 2 примера понятий, суждений, умозаключений из курсов математики, истории, информатики.
   Перечислите существенные признаки, составляющие содержание понятий: квинтэссенция; добродетель; истина; ложь (используйте толковый словарь)
2. Определите правильность следующего рассуждения: Сидящий встал; кто встал, тот стоит; значит, сидящий стоит.
3. Выведите, если это возможно, заключение из каждой пары посылок:
   1) Тем, кто лыс, расческа не нужна. Ни одна ящерица не имеет волос.
   2) Ни один добрый поступок не является незаконным. Все, что законно, можно делать без страха.
   3) Некоторые уроки трудны. Все, что трудно, требует внимания.

Привести примеры мыслей-понятий,суждений и умозаключения.

Формы мышления — это формальные структуры мыслей. Различаются три формы мышления — понятие, суждение и умозаключение.

Понятие — форма мышления, в которой отражаются общие и при том существенные свойства однородной группы предметов и явлений.

Понятие существует в виде значения слова, обозначается словом. Каждое слово обобщает. В понятиях наши знания о предметах и явлениях действительности кристаллизуются в обобщённом и отвлеченном виде. В этом отношении понятие существенно отличатся от восприятия и представлении памяти: восприятие и представление конкретны, образы, наглядны: понятие обладает обобщённым, абстрактным, ненаглядным характером.

Восприятие и представление всегда есть отражение конкретного, единичного. Никто из нас никогда не видел и не может видеть книги, собаки, человека, дерева и любого другого предмета вообще, так как нельзя представить себе предмета, абсолютно лишённого каких-либо индивидуальных признаков. А мыслить об этом можно.

Суждение — определённое знание о предмете, утверждение или отрицание каких-либо его свойств, связей и отношений. Формирование суждений происходит как формирование мысли в предложении. Суждение — такое предложение, в котором утверждается взаимосвязь объекта и его свойств. Связь вещей отражается в мышлении как связь суждений. В зависимости от содержания отражаемых в суждении предметов и их свойств различаются следующие виды суждения: частное и общее, условное и категорическое, утвердительное и отрицательное.

Суждение раскрывает содержание понятий, т. е. знать какой-нибудь предмет или явление — значит, уметь высказать о нём правильное и содержательное суждение, то есть уметь судить о нём.

В суждении выражаются не только знания о предмете, но и субъективное отношение человека к этому знанию, различная степень уверенности в истинности этого знания.

Психологическими аспектами суждения являются мотивация и целенаправленность суждений индивида.

Рассуждение — это работа мысли над суждением. Рассуждение является обоснованием, если исходя из суждения оно вскрывает посылки, которые обуславливают его истинность.

Рассуждение является умозаключением, если исходя из посылок оно раскрывает систему суждений, следующую из них.

Умозаключение — такая форма суждения, в процессе которой человек, сопоставляя и анализируя различные суждения, выводит из них новое суждение.

Умозаключение — Гуманитарный портал

Умозаключение — это мыслительная процедура непосредственного выведения некоторого высказывания из одного или нескольких [других] высказываний (см.  Высказывание). При этом высказывания, из которых делается вывод, называют посылками(или аргументами) умозаключения, а высказывание, которое выводится из посылок, — заключением. Умозаключение представляет собой особый вид рациональной мыслительной деятельности человека (см. Мышление) с обобщённым причинно-следственным значением, позволяющий с помощью языковых средств (см. Язык) осуществлять обоснование утверждения или системы утверждений, либо получение нового вывода (см. Логический вывод) из нескольких посылок, опираясь на некоторое известное знание и используя различные логические методы преобразования имеющейся информации. В этом смысле умозаключение является простейшей разновидностью рассуждения (см. Рассуждение) — процедуры обоснования высказывания посредством пошагового выведения его из других высказываний; в умозаключении переход от аргументов (их роль играют посылки) к обосновываемому тезису (заключению) происходит в один шаг. Умозаключения играют исключительно важную роль в процессах познания, так как они позволяют получать новые знания без непосредственного обращения к опыту. В логике (см. Логика) умозаключение принято формулировать следующим образом: Где над чертой записываются посылки, под чертой — заключение, а сама черта выражает акт выведения заключения из посылок. Выделение в умозаключении посылок и заключения и установление его структуры составляют его логический анализ. В логике традиционно считается, что всякое правильное умозаключение должно удовлетворять условию: если его посылки истинны, то должно быть истинным (или правдоподобным) и заключение. Это условие соблюдается, если в ходе умозаключения не нарушаются законы логики и правила вывода. В реальном процессе мышления часто опускаются некоторые из посылок умозаключения и явно не формулируются правила вывода и законы логики, лежащие в его основе, либо умозаключение имеет энтимематический характер, то есть когда оно не выражается в полном виде, а какая-то его часть (посылка, заключение), подразумеваясь, опускается (см. Энтимема). Всё это открывает возможность ошибок в умозаключениях. Логика устанавливает способы отличения правильных умозаключений от неправильных и тем, в частности, способствует предупреждению и исправлению логических ошибок (см. Логические ошибки). Обычно рассуждения и доказательства представляют собой цепи умозаключений, в которых заключение предшествующего умозаключения становится посылкой одного из следующих за ним. Условием правильности доказательства является не только истинность его исходных суждений — оснований доказательства, но и правильность каждого входящего в его состав умозаключения. Умозаключения, совершающиеся по одним и тем же правилам вывода и законам логики, считаются умозаключениями одной и той же логической формы. По своей форме умозаключения разделяются на несколько видов. По степени обоснованности выведения заключения из посылок умозаключения принято делить на демонстративные и недемонстративные. В демонстративных умозаключениях одновременная истинность посылок обеспечивает получение истинного заключения, информация заключения составляет в них часть совокупной информации посылок. В недемонстративных умозаключениях, напротив, при переходе от посылок к заключению имеет место приращение информации, однако одновременная истинность посылок не гарантирует истинности заключения. Наиболее важной и обширной разновидностью демонстративных умозаключений являются дедуктивные умозаключения (см. Дедукция). Между их посылками и заключением имеет место отношение логического следования (см. Логическое следование), то есть сама логическая форма этих умозаключений обеспечивает сохранение истинности при выведении заключения из посылок. В демонстративных умозаключениях других типов (к ним относятся, например, математическая индукция, полная индукция, строгая аналогия) достоверность вывода, получаемого из истинных посылок, обусловлена не только логической формой входящих в умозаключение высказываний, но и значениями содержащихся в них дескриптивных терминов, особенностями универсума рассуждения. Среди недемонстративных умозаключений наибольший интерес представляют так называемые правдоподобные, или вероятностные, умозаключения, к которым относятся, например, обратная дедукция, неполная индукция, нестрогая аналогия, статистические выводы. Правдоподобные умозаключения характеризуются наличием отношения логического подтверждения между посылками и заключением. Данное отношение имеет в современной логике множество различных экспликаций. Так, широкое распространение получила трактовка отношения подтверждения в соответствии с критерием позитивной релевантности: посылки подтверждают заключение, если и только если вероятность истинности заключения возрастает (но не становится равной единице) при условии одновременной истинности посылок. Основной сферой применения дедуктивных умозаключений являются точные науки (прежде всего математика и математическая логика), в которых особые требования предъявляются к строгости доказательств. Правдоподобные умозаключения, главным образом, используются в эмпирических науках для выдвижения и верификации гипотез, получения законоподобных утверждений, относящихся к исследуемой предметной области. В целом, проблема классификации умозаключений не получила в логике однозначного решения, существенные различия в этой классификации зависят от разных подходов к логическому знанию: типы умозаключений изучались в зависимости от тех аспектов оформления мыслительных процессов, которые анализировались в данный культурно-исторический период; менялись принципы обоснования последовательного описания как самих умозаключений, так и взаимоотношений между ними; менялись научные стандарты логических исследований.

«Все ваши друзья — гусеницы». Что такое логика, и как она спасает от безумия? – Православный журнал «Фома»

Приблизительное время чтения: 25 мин.

«Все гусеницы едят капусту. Все мои друзья едят капусту. Следовательно, все мои друзья – гусеницы». Что в этом умозаключении не так? Об этом и не только рассказывает Дмитрий Гусев, доктор философских наук, профессор МПГУ, РАНХиГС, Московского университета им. С. Ю. Витте.

Здравствуйте, уважаемые зрители и слушатели. Меня зовут Дмитрий Гусев. Я — преподаватель Московского государственного педагогического университета (МПГУ), РАНХиГС и Московского университета им. С. Ю. Витте.

 

Расшифровка:

Мы начинаем нашу лекцию, тема которой — «Когда дважды два — не четыре, а лжец говорит правду, или Зачем нам изучать логику». Есть три формы мышления, в философии это называется три уровня рационального познания мира, три ступени рационального познания. В логике — три формы мышления: понятие, суждение и умозаключение. Вот они, три формы мышления.

Что такое понятие? Понятие — это форма мышления, которая отражает или представляет объект окружающего мира или его признак. Это то, что в языке у нас представлено словом или словосочетанием. В окружающем нас мире есть огромное количество объектов и признаков объектов, а мы каждый признак как-то именуем, как-то называем. Мы говорим: вот это рыба, это учебник, это белизна, это мужество, это космонавт, это планета. Вот это все: человек, космонавт, планета, мужество, учебник, белизна — это все примеры понятий. Понятия — имена вещей окружающего нас мира или имена признаков окружающего нас мира. Это что такое понятие. Понятие — как бы логический атом. Понятие лежит в основе мышления. Иногда говорят: мышление человека понятийное, то есть основанное на этих понятиях.

Если несколько понятий соединить между собой, из них получится суждение. Суждение — вторая форма мышления. Возьмем два понятия. Понятие «карась» и понятие «рыба». Соединим их между собой: все караси являются рыбами. Вот это уже суждение. Можно по-другому соединить: некоторые рыбы являются карасями. Это другой пример соединения. И вот это: все караси являются рыбами, некоторые люди — спортсмены, все планеты — не звезды, — вот это примеры суждений. Суждение — вторая форма мышления.

И, наконец, если несколько суждений между собой соединить так, чтобы из исходных суждений вытекало новое суждение, это будет называться умозаключение. Пример умозаключения — это то, что мы с вами уже сегодня рассмотрели. Первое суждение: все планеты движутся, второе: Земля — это планета, следовательно, Земля движется. Это все, вместе взятое, называется умозаключение. Или помните второй пример? Все дети обладают мышлением, взрослые — не дети, значит, они не обладают мышлением. То есть в умозаключении вывод может из посылок вытекать как истинный, так и ложный.

Итак, три формы мышления: понятие, суждение и умозаключение. Логика — наука о формах и о законах правильного мышления. А что такое законы мышления? Законы мышления — это такие принципы или правила, причем объективные… вот тут важно подчеркнуть: что значит — объективные? Объективные — значит, сами по себе существующие, от нас не зависящие. Наше мышление так устроено, что оно протекает в соответствии с этими законами, с этими принципами, с этими требованиями. Законы логики объективны в том смысле, что они не зависят ни от пола, ни от возраста, ни от исторической эпохи, ни даже от уровня образования. Откуда они берутся, эти законы, эти принципы мышления? Никто не знает. Тут могут быть разные варианты. То ли закладываются в сознание человека самим Богом, чтобы человек мыслил по этим законам и в соответствии с ними. То ли они формируются стихийно в процессе эволюции, но это уже вопрос другой. Главное, что есть эти принципы, эти законы, по которым протекает человеческое мышление. И что интересно, человек, который даже логику не изучал, который с ней не знаком, все равно в целом стихийно эти законы соблюдает. Это называется интуитивная логика, которой все мы владеем задолго до того, как идем в школу учиться. Давайте приведем какой-нибудь пример. Допустим, вот такая ситуация:

— Что делаешь, когда долго заснуть не можешь?

— Как что, я обычно считаю.

— О, считаешь, здорово, до скольких считаешь?

— До трех.

— До трех? Так мало?

— Не, иногда я и до полчетвертого считаю!

Обратите внимание, любой человек, независимо от пола, возраста, национальности, что скажет? Почему получилась нелепая ситуация? Почему получился комический эффект? Потому что здесь любой человек что скажет? Разный смысл вкладывают в одни и те же слова, правильно? Если говорить языком логики, в этом примере был нарушен первый закон логики — закон тождества. Человек может не знать про закон тождества, не знать, как он нарушается, но, когда он нарушается, он это чувствует. Он это видит мысленным каким-то взором. О чем это говорит? О том, что он уже этим законом пользуется. Уже этот принцип мышления как бы вмонтирован в его мышление каким-то образом с незапамятных времен, и вот — срабатывает в нем.

Или, например, вам скажут: «Поедем завтра вечером на рассвете». Вы скажете: «Как это?» А вот так — поедем завтра вечером на рассвете. Он был молодой человек преклонного возраста. «Дело было в январе — пятого апреля, Жарко было на дворе — мы окоченели». «Жив, здоров, лежу в больнице, Сыт по горло, есть хочу. Приезжайте ко мне в гости — Я вас видеть не хочу». Вы скажете: «Так, ну такого не может быть. Если он молодой, то он не старый, если вечером, то точно не на рассвете». И когда вы так говорите, вы стихийно соблюдаете второй закон логики — закон противоречия. Указываете на его нарушение. Допустим, не знаем об этом законе, но когда он нарушается, говорим: да, вот действительно, что-то здесь не то.

А вот например такая ситуация:

— С чего ты это взял?

— Товарищ рассказал.

— А вдруг он тебя обманывает?

— Да он не может меня обманывать! Какой смысл ему меня обманывать?

Слышали, да? Он мне это рассказал, какой смысл меня обманывать. Я в Интернете прочитал, значит, это правда, в этом невозможно усомниться. Раз так там написали, значит, так и есть на самом деле. Вы говорите: ну не факт, не обязательно, из того, что там так написали, не следует, что так на самом деле. Мало ли что можно там написать, мало ли что тебе товарищ сказал. Когда мы так говорим, мы стихийно соблюдаем четвертый закон логики — закон достаточного основания. Не зная об этом законе, тем не менее пользуемся им — на интуитивном уровне.

А вот очень хороший пример. Всем знакомо такое явление, как составление классификаций. Что такое составление классификаций? Это деление какого-то одного объема на какие-то новые объемы. Например, люди бывают мужчинами и женщинами. Это высказывание — это простая, примитивная, но уже классификация. Или: учебные заведения делятся на начальные, средние, высшие. Вот это уже классификация. Вот кто-то скажет: «Люди бывают мужчинами, женщинами, неграми и учителями». Вы скажете: «Так, что-то тут не то». А почему не то? Люди бывают мужчинами? Да. Женщинами? Да. Неграми? Да. А учителями? Тоже. Вы скажете: «Ну не только же ими». Хорошо, не только, поправимся: люди делятся на мужчин, женщин, негров, учителей и так далее. И других людей. Всё! Вроде бы как теперь классификация полная. Вы говорите: «Опять неправильно». Почему неправильно? Вы скажете: «Ну потому что здесь вы в кучу смешали пол, расу и профессию». Я вас спрошу: «А что, нельзя смешивать?» Вы скажете: «Нельзя». Вопрос: почему нельзя? Кто сказал, что нельзя? Где мы это проходили, что нельзя? Мы в школе точно проходили: на ноль делить нельзя. Помните? «Не» с глаголом писать слитно нельзя. А в какой это науке было, что нельзя при классификации смешивать признаки и говорить, что люди бывают мужчинами, женщинами, неграми и учителями? Этого не было нигде. Этому нас никто не учил. Но мы точно знаем, что нельзя. На самом деле в примере, который прозвучал, была допущена ошибка — подмена основания в делении понятия. Но не каждый же человек знает, что это подмена основания в делении понятия? Он может не знать про эту ошибку, не знать про это правило, не знать про это деление понятия, объем понятия, содержание понятия, но когда ошибка эта возникает в каких-то эпизодах мышления речи, он это чувствует. О чем это говорит? О наличии у нас той самой интуитивной логики.

Итак, законы логики — объективные правила или принципы, не зависящие ни от каких наших субъективных особенностей, соблюдение которых в мышлении речи позволяет нам из истинных суждений выводить всегда истинные выводы, не зависимые от содержания.

А теперь расскажем немножко о том, что такое закон логики, который называется закон тождества. Это первый закон логики. С моей точки зрения, это главный закон логики. Я даже думаю, что не исключено, что остальные законы логики можно вывести из этого самого закона тождества. Мысль, конечно, спорная, но кто знает.

Закон тождества — это, иначе говоря, закон чего? Равенства. Тождество — это равенство, правильно? И звучит закон тождества так: любая мысль должна быть тождественна самой себе. А как понимать: тождественна — себе? Очень просто. Она должна быть ясной, определенной, однозначной, недвусмысленной. В рассуждении нельзя подменять и путать понятия, в рассуждении нельзя уклоняться от темы, нельзя употреблять одни и те же слова в разных смыслах или вкладывать один и тот же смысл в разные слова. Иначе говоря, по закону тождества равное должно быть равным, а неравное должно быть неравным.

Давайте приведем простой пример, который покажет нам, что такое закон тождества.

Возьмем простое высказывание: «Ученики прослушали учителя». Вот такое высказывание, вот такое суждение. Если ничего не добавить к этому высказыванию, если не сделать никаких дополнительных комментариев, найдется ли на свете такой человек, который точно скажет, о чем идет речь в этой фразе. Вообще никто сказать не может. А почему? Потому что если никаких дополнительных комментариев не сделать, то получается, что речь идет то ли о том, что ученики всё слышали, то ли о том, что ничего не слышали. Высказывание одно, возможных смыслов минимум два. Я, кстати, в своей практике многолетней преподавательской этот пример приводил студентам. И говорил: «Вот смотрите, ученики прослушали объяснение учителя: одна фраза — два разных смысла». Мне как-то студенты сказали: «Почему два?» Они же могли его вот так прослушать — фонендоскопом. Доктор прослушивает больного. Да. Они могли устройство установить у учителя в кабинете прослушивающее и так его еще прослушать. Получилось уже четыре смысла. Ну, как минимум — их два. Итак, что получилось: одно высказывание, смыслов возможных два. Один не равно двум. Тут очень простое объяснение закона тождества. Один не равно двум, «равно» зачеркнуто, отсутствие тождества. Нетождественность, неравенство одного другому. Вот нарушение закона тождества.

«Из-за рассеяности шахматист часто терял очки на турнирах». Если ничего не добавить к этому высказыванию, сможет кто-нибудь сказать, о чем идет речь в этой фразе? Тоже нет. То ли вот такие очки, которые на носу мы носим, то ли спортивные баллы. Опять: одна фраза — два смысла, закон тождества нарушается. Можно сказать иначе. «Ученики всё слышали» — первое. Второе — «Ученики ничего не слышали». Эти две ситуации друг другу тождественны? Они друг другу не тождественны. Потому что «всё слышали» и «ничего не слышали» — это разные вещи. Но фраза-то была одна. Поэтому что получается? Нетождественное как бы незаметно отождествляется. Или неравное незаметно уравнивается. Нарушается закон тождества. В результате нарушения закона тождества появляется какое суждение? Неясное суждение. «Ученики прослушали учителя». Неясное суждение.

Но неясное суждение — это еще не самые страшные или, можно сказать, плохие последствия нарушения закона тождества. На нарушении закона тождества строятся такие знаменитые логические явления, как софизмы. Знаменитое слово греческое, не только в логике, в культуре… Что такое софизмы? Мы с вами знаем, что софизмы — это интеллектуальные фокусы, уловки. Само слово «софизм» с греческого переводится как уловка, подвох. Софизм — это внешнее правильное доказательство какой-то ложной мысли с помощью преднамеренного нарушения законов логики. Уточним: с помощью нарушения закона тождества. Любой софизм построен на нарушении закона тождества.

И вот теперь — как строится любой софизм? Каким образом? Какова анатомия софизма? Анатомия очень простая. Берутся две ситуации — нетождественные, заведомо нетождественные. И рассуждение строится так, что в рассуждении они незаметно отождествляются. Что-то нетождественное отождествляется. Что-то неравное уравнивается. Что-то не одно и то же представляется как одно и то же. Вот очень простой пример. Три и четыре — разные числа? Да. Три и четыре — это семь? Значит, семь — разные числа. Логично, хочется сказать. По крайней мере, внешне рассуждение выглядит правдоподобным, вроде бы как правильным. Три и четыре — это же два разных числа. А три и четыре — это семь. Кстати, союз «и» мы обычно всегда употребляем, когда речь идет про сложение. Правильно? Два и три — это восемь. Мы же не говорим: два или три — это восемь. Два и три — это восемь. Три и четыре — это два разных числа. Три и четыре — семь. Значит, семь — это два разных числа. Что произошло? Берется первое — простое перечисление натуральных чисел, это первая часть нашего рассуждения. «Три и четыре — это два разных числа» — простое перечисление чисел. И дальше берется второе — сложение чисел. «Три и четыре — это семь». Вторая часть фразы — сложение чисел. А теперь: простое перечисление чисел и сложение чисел — одно и то же? Не одно и то же. А мы это не одно и то же представили как одно и то же. Мы разное представили как одинаковое. Мы нетождественное незаметно отождествили. О чем говорит закон тождества? Равное должно быть равным. А неравное должно быть неравным. В нашем примере неравное было равным. И вот получилась видимость правильного доказательства ложной мысли.

Еще очень хороший пример. Ребенка спросили: «Скажи, пожалуйста, сколько лет твоему отцу?» Он сказал: «Моему отцу столько же, сколько и мне». — «Как такое возможно?» — «Судите сами: мой отец стал моим отцом только когда? Только тогда, когда я родился. Правильно? До моего рождения он же не был моим отцом? Не был. Значит, сколько лет моему отцу? — Столько же, сколько мне». Логично, нет? Конечно, логично. Что произошло? Здесь некое «а» — здесь некое «б». Здесь возраст человека, а здесь, как вы догадываетесь, стаж отцовства. Так сформулируем это второе. Возраст человека и стаж отцовства — одно и то же? Не одно и то же. Нетождественные объекты? Нетождественные. А представлены в рассуждении как какие? Как тождественные. Нетождественное в рассуждении незаметно отождествляется. И получается видимость правильного доказательства ложной мысли. Получается софизм. Вот еще один пример.

А вот очень хороший софизм, который звучит так. Помните из курса физики: все тела при нагревании расширяются, а при охлаждении сжимаются. Что такое лед? Лед — это вода замерзшая, значит, сжавшаяся. Ну а раз она сжавшаяся, значит, плотность льда больше, чем плотность воды. Раз сжавшаяся вода. Но раз плотность льда больше, чем плотность воды, то любой кусочек льда, образовавшись на поверхности воды, должен немедленно в ней тонуть. Мы помним из курса физики: если плотность больше — значит, сразу тонет. Но если плотность меньше, то плавает, вернее, на поверхности находится. Кусочек льда немедленно должен тонуть. Но тогда водоемы в принципе не должны замерзать. Ледяной покров должен образовываться над самым дном водоема, но не сверху. А они почему-то замерзают. Как же так? Что же это такое? Почему так получается? Это рассуждение с подвохом, разумеется. Рассуждение софистическое. Но тем не менее внешне оно выглядит вполне правдоподобно. А если мы подпрыгнем, как стоим в комнате, так и подпрыгнем, оттолкнувшись двумя ногами от пола, мы приземлимся примерно в ту же точку, от которой оттолкнулись. В ту же самую. Но если мы подпрыгнем в вагоне быстро движущегося поезда, то за время, пока мы будем находиться в воздухе, пусть там за какие-то полсекунды, полвагона успеет немножко уйти вперед, он же движется. И мы приземлимся не в ту точку, от которой оттолкнулись, а немножко позади нее. Еще раз подпрыгнем, еще немножко дальше приземлимся. Поэтому, если мы находимся в вагоне быстродвижущегося поезда, нам совсем не надо из конца в конец вагона ходить, нам достаточно попрыгать на месте, пока нас не снесет в нужную сторону. Ну так получается. Вы скажете: «Нет, там нужно ходить точно так же». — «Как? Точно так же ходить, как в этой комнате?» Мы едем в вагоне, поезд движется со скоростью 300 км/ч. И нужно туда-сюда ходить так же, как в этой комнате? Эта комната, получается, тождественна этому поезду, который движется с такой скоростью, но нет же ведь! Она же неподвижна. А там движется. Или он тогда неподвижен? Что-то не складывается. Ну, по крайней мере, тоже хороший пример.

А помните, Земля движется вокруг своей оси? Длина экватора — 40 тысяч километров примерно. Оборот вокруг оси за 24 часа. Поделим 40 тысяч на 24 часа. У нас получится скорость 1600 километров в час. Пока никакого подвоха нет. Каждая точка земного экватора движется вокруг земной оси со скоростью 1600 километров в час примерно. Теперь на экваторе проложен рельсовый путь. По экватору поезд едет по этим рельсам. Поезд только едет в сторону, противоположную вращению Земли. Земля вращается в одну, а поезд — в другую. Значит, этому поезду, чтобы прибыть к месту назначения, нужно двигаться со скоростью больше, чем 1600 километров в час, иначе его будет сносить постоянно туда, в сторону вращения Земли. Поэтому на экваторе нет железных дорог. И поезда там не ходят.

Или второй вариант. Поэтому на экваторе ходят такие суперпоезда, которые развивают гораздо большую скорость.

Понятно, что и первое — чушь, и второе — чушь, но тем не менее… Вопрос какой-то, проблема какая-то есть. Это тоже всё софистические рассуждения. Итак, софизмы — это такие рассуждения, в которых преднамеренно нарушается закон тождества, и рассуждение внешне выглядят правильно, хотя мысль в нем доказывается ложная.

Но это первая разновидность софизмов. Вторая разновидность — это софистические задачи. Софистические задачи, загадки различные, головоломки и так далее. Есть просто задачи, которые нужно решать, а есть задачи софистические, когда решать ничего не надо, а надо как бы разоблачить условия или показать, где здесь был подвох. Вот самый простой пример давайте приведем. Задача такая: этим заканчивается и день, и ночь. Что это такое? Начинаешь ломать голову. А что это такое? И день, и ночь этим заканчивается… Отдыхом, сном? Закатом, рассветом? Учебой, похмельем? Чем заканчивается? И когда мы слышим ответ, мы испытываем дискомфорт, удивление какое-то, может быть, даже недоумение. Мягкий знак! А попробуйте сказать, что не заканчивается этим и день, и ночь! Этот дискомфорт внутренний, который возникает в ряде вопросов, загадок, задач, он опять говорит, что в нас опять работает интуитивная логика. Мы не знаем про закон тождества и софизмы, но когда этот происходит, мы это чувствуем. Правильно? Итак, что произошло? Берется реальное время суток и берется слово. Время суток и слово. Тождественны объекты? Не тождественны. Они незаметно отождествляются и получается видимость какой-то хитроумной задачи. Или какого-то хитрого вопроса.

Помните знаменитые с детства вопросы? Почему люди ходят в сапогах? По земле. На балконе ходят? Если балкон не в аварийном состоянии, то, конечно, ходят. А на самом деле: на бал кони не ходят, кто ж коней пустит на бал. На бал кони точно не ходят. Мы скажем: это же игра слов. Правильно. На уровне повседневного мышления — игра слов, подмена понятий. В логике — нарушение закона тождества. Потому что мы берем две ситуации нетождественные и незаметно их отождествляем. Вот еще хорошая задача: как разделить 12, чтобы получилось 7 без остатка. Это задача даже из учебника — по математике, для третьего класса. Но задача софистическая, которая помещена в раздел обычных задач. Там не никаких комментариев, что она особенная задача. Ее нельзя решать традиционно. Как 12 разделить, чтобы получилось 7 без остатка? Ребенок честно пишет: 12 разделить на икс, равно семь. Дальше: икс равно 12 разделить на 7. Так? Говорит: ну вот не решается задача. Оказывается, составители учебника вот что имели в виду: нужно 12 вот так начертить — XII римскими. И проводится горизонтальная линия. Делится XII римскими пополам. И сверху образуется римская цифра семь. И без остатка. Но это софистическая задача! Почему? Потому что человек начал решать ее математически, составляя уравнение, а она решалась графически. Математическое решение и графическое нетождественны друг другу, нетождественны. Отождествили нетождественное. Получилось что? Видимость правильного доказательства, ложной мысли. Вторая разновидность софизмов — это софистические задачи.

Третья разновидность софизмов — это комические ситуации. Авторы литературных произведений иногда преднамеренно нарушают законы тождества в своих произведениях, чтобы придать повествованию некую комичность. Помните знаменитого Ноздрева из «Мертвых душ». Автор говорит: «Ноздрев был… исторический человек». Помните? Исторический человек. Мы начинаем думать: выдающийся, знаменитый, историческая личность. Полководец, император. А дальше: где бы он ни появлялся, с ним всегда случалась какая-нибудь история. Скандальная история. Мы видим одно слово или одно понятие, которое используется в разных смыслах, нетождественное отождествляется. И возникает видимость чего? Комического эффекта. Достоевский, роман «Бесы»: «Липутин держал всю свою семью в Божьем страхе и взаперти». Впоследствии Степан Трофимович Верховенский стал впадать не только в гражданскую скорбь, он еще впадал периодически в шампанское. Он впадал в гражданскую скорбь и в шампанское. Юлия Михайловна должна была встать со своего ложа в негодовании в бигудях. Этот тоже нарушение закона тождества, которое преднамеренно использует автор для предания комического характера повествованию.

Ну и, наконец, известные комические ситуации, которые мы с вами сегодня рассматривали. Помните? «Ты что делаешь, когда долго заснуть не можешь?» — «Я считаю». — «До скольки?» — «Ну как — до трех». — «Что так мало?» — «Ну, бывает, до четырех часов считаю». Понимаете, о чем идет речь? Нарушение закона тождества. Почему человек открывает йогурт прямо в магазине? Потому что на упаковке написано «Открывать здесь». Ну как — написано и открываю. Все пооткрывал. Менеджер подходит, говорит: «Вы что наделали?» — «Как — что я наделал? Написано: открыть здесь — я здесь и открыл». И не придерешься, кстати говоря. Если даже меня привлекут к ответственности административной, еще не факт, что я не смогу отстоять свой интерес в суде. И тогда производителю или менеджеру магазина придется писать, что имеется в виду. А почему человек выпил и пищит? Выпивает таблетку и пищит. Потому что написано: «После приема пищи». Вот я и пищу. Перед «пищи» никакой знак препинания не ставится. После приема — пищи, сказано — я и пищу. Нормально же?

«Почему вы называете этот хор смешанным? Ведь в нем одни женщины». — «Ну да, только одни из них умеют петь, а другие не умеют, поэтому хор смешанный».

«У вас в гостинице есть тихие номера?» — «У нас все номера тихие, только жильцы бывают шумные».

«Ты умеешь нырять?» — «Умею нырять». — «А под водой долго сидишь?» — «Пока кто-нибудь не вытащит, сижу».

«А он на чем сюда приехал?» — «На BMW, он на “мерседесе”, а он — на электричке». — «Он что, бедный, что ли, чтобы на электричке ездить?» — «Он не бедный, но ему родители сказали: нечего к роскоши привыкать, пусть, как все обычные люди, поездит на электричке. Ну, и купили ему электричку».

А вот смотрите — строчка из объявления о знакомстве: «А еще я увлекаюсь фотографией. Только мама ее все время куда-то прячет». Это вот еще одна комическая ситуация. Итак, комические ситуации эти тоже основаны на нарушении закона тождества. Каким образом? Берутся вещи нетождественные, незаметно отождествляются.

И, наконец, не только неясное суждение, не только софистические задачи, не только комические ситуации, но и многие фокусы тоже основаны на нарушении закона тождества. Потому что тот, кто производит фокус, он знает, как это делается, тот, кто смотрит, он не знает, как это делается. Знание нетождественно незнанию, и вот из этой не тождественности, как раз и возникает эффект чего-то необычного, чего-то удивительного. Как это он это делает, интересное дело. Кстати говоря, всем знаком такой фокус интеллектуальный про отгадывание чисел? Детский такой, но тем не менее. Задумай число, сделай такие-то действия, а потом я скажу, какой результат. Все знают, на чем он основан или нет? Задумайте число не очень большое, какое-нибудь, чтобы просто было считать, производить с ним манипуляции. И прибавьте к нему 6. Потом отнимите от этого два. Потом к этому прибавьте 8. И к этому 4. Потом от этого отнимите задуманное. То, что получилось, разделите на два. Отнимите от этого три. У вас получилось пять. А как так получилось? Я говорил: задумайте число. А потом где-то в середине прозвучало: отнимите задуманное. То есть число, которое задумал человек, — это икс, потом этот икс вы отняли. Х минус х сколько будет? Будет ноль. А все остальное, что вы делали от и до, все вам уже известно. Но — человек может этого не знать, и ему может показаться: ничего себе, как это он так? А теперь смотрите, если у вас есть под рукой калькулятор, телефон, я даже вас сейчас об этом попрошу. Напишите там трехзначное число. Любое. 357. И запишите его вправо, просто без знаков препинания, чтобы получилось шестизначное. 357 357. Чтобы получилось число такого вида. Я не знаю, какое число вы записали. Но я говорю: «Если это число шестизначное, которое вы сейчас записали, вы разделите на 11, то я могу гарантировать, что деление будет без остатка». А вы можете сказать: «Как вы можете гарантировать, вы же не знаете, какое число…» Не знаю. Но точно у всех без остатка. А теперь то, что осталось, разделите на 7 и деление тоже будет без остатка. И это можно гарантировать. Без остатка? А теперь то, что получилось, разделите на 13. И деление не только будет без остатка, но вы получите то, что было задумано. Правильно? Получилось? Как он это делает? Что это такое? Почему так получается? Давайте раскроем секрет этого фокуса. Этот фокус называется «число Шахерезады». Число Шахерезады — 1001. Произведение трех чисел… Помните, как Герман запоминал три карты — тройка, семерка, туз. Так запомните три числа: 7, 11, 13. Произведение трех чисел 7, 11, 13 дает в результате 1001. Любое трехзначное число, умноженное на 1001, дает число вида abc abc, если любое трехзначное число вы умножите на 1001, вы получите 357 357. Если это число вы разделите на 13, 11, 7, на 7, 11, 13, на 11, 7, 13… Неважно, в какой последовательности вы разделите его на эти множители, вы получите исходное. Вы понимаете? Можете запомнить эти три числа, потом даже в разных комбинациях предлагать собеседнику.

Вот, пожалуйста, мистическое, магическое число…

И это тоже нарушение закона тождества, потому что получается, что один знает, как это делается, другой не знает, как это делается. И вот на этом «знает» и «не знает», на этой нетождественности как раз и возникает эффект этого необычного.

Теперь давайте подведем итог. Итак, главный закон логики — закон тождества. Согласно закону тождества, любая мысль должна быть тождественна самой себе, равной самой себе, если она самой себе не равна, то возникают неясные суждения, возникают софизмы, возникают комические ситуации, софистические задачи и даже различного рода фокусы.

Итак, важное логическое явление — это софизмы, преднамеренные логические ошибки. Есть в логике ошибки непреднамеренные, которые допускаются по незнанию, по невнимательности. Они называются паралогизмы. И разница между софизмами и паралогизмами в том, что софизмы — ошибки умышленные, паралогизмы — неумышленные, непреднамеренные. А еще есть в логике такое удивительное явление, которое называется парадоксами. Но парадоксы — это уже совсем другое. А пока, поскольку тема нашей лекции была «Когда дважды два — не четыре», об этом-то ничего не было сказано в данном случае.

Возьмем спичку, сломаем ее пополам. А потом одну из этих половинок тоже сломаем пополам, понятно, что кусочков получится три. Но мы сделали два раза по два. В нашем эксперименте два раза по два сколько будет? Три. Дважды два — три. Понятно, что это софизм. Первая часть названия нашей лекции «Когда дважды два — не четыре», она посвящена тому, что такое софизмы. А три раза по два — сколько должно быть? Три раза по два должно быть шесть. Докажем, что не шесть, а как раз — четыре. Берем спичку ломаем пополам. Один раз два. Ломаем первую половинку. Второй раз два. Оставшуюся половинку ломаем. Третий раз два. Три раза по два — раз, два, три, четыре. Но это тоже софизм. Что здесь произошло? Операция деления по два и операция умножения на два — разные вещи? Разные вещи. А мы их незаметно отождествляем. И у нас получается видимость правильного доказательства ложной мысли. А если сформулировать этот парадокс на другом языке? Это называется метаязык. То есть выйти в метаязык и из этого языка рассматривать. Тогда там, получается, все вроде как решается. Но опять же, видите: если на другом языке сформулировать и потом между языками сделать перекличку — вот тогда получится. А если этого не делать? Если не делать — не получится. Это как один вариант. Вариантов существует очень много. Если их сейчас разбирать, то можно только запутаться. Но наша задача помнить, что парадокс — это именно логический тупик, а софизм — это подвох, это уловка. И любой софизм разоблачаем вот так: что с чем отождествляется, будучи нетождественным, правильно? Является эта ситуация софизмом или парадоксом? Давайте попробуем вместе ответить на этот вопрос. Это конкретная ситуация.

«Тогда назовем, когда будут все. А пока нет всех — нет толка. Но какие-то есть». Парадокс или софизм? Это ситуация, конечно, является софистической. Конечно, это такой логический фокус. Но в данном случае, что с чем отождествляется, будучи нетождественным? «Есть все» и «нет всех». А это некое Б, ситуации тождественные? Нетождественные, а представлены так, как будто они тождественные. То есть мы опять незаметно отождествляем что-то нетождественное. И нарушаем таким образом закон тождества. Кстати, закон тождества нарушается сплошь и рядом. Даже в нашей повседневной жизни.

Вы договорились встретиться с товарищем в три часа. А он пришел полчетвертого. И что такого — полчетвертого пришел. Вы договорились в три? В три. А он пришел полчетвертого. Полчетвертого — это три? Нет. Он нарушил закон тождества. Это нетождественные ситуации: три — это три, а полчетвертого — это полчетвертого. Он что-то кому-то пообещал — единица. Обещание не выполнил — ноль. Единица и ноль — знак равенства можно поставить? Нельзя. Обещал и выполнил. Единица и единица, закон тождества соблюден. Дальше. «Обещай мне это». — «Прости, не могу». Не могу обещать, я не обещал тебе — ноль, ну и не выполнял то, что не обещал, — тоже ноль. Ноль и ноль — закон тождества выполнен? Выполнен. Когда договорились в три, а я пришел полчетвертого… Причем, как я пришел полчетвертого? Мне говорят: «А почему ты полчетвертого пришел?» А я говорю: «Так получилось». Обратите внимание. Всем знакомая фраза? Так получилось. Я не говорю: прости, форс-мажор, меня остановили полицейские, я сломал ногу… У меня так получилось! А когда вы спрашиваете: «А как у тебя так получилось?», я что отвечаю? «А я не знаю, как так у меня получилось, я ничего не могу с собой сделать». Вот, пожалуйста. Вот после этого и попробуйте говорить, что человек —это звучит гордо. Ничего себе гордо. Я, взрослый адекватный человек, говорю: «Так у меня получилось». Причем я все рассчитал: во сколько выйти, сколько ехать — и я опять опоздал. Ну чего такое? Так получилось. Я твердо решил: завтра точно не опаздываю. И точно мне нужно было выйти без десяти, а я вышел через двадцать минут. Как так? А получилось. Чувствуете? Ничего себе «гордо звучит». Какая-то действительно родовая поврежденность, изначальная испорченность. Ну если бы я был ненормальный, нетрезвый… Но это же в здравом уме. В твердой памяти. Будучи взрослым человеком. Каждый день обещаю выйти вовремя и опять, и опять, и опять выхожу позже. Это какая-то заколдованность— это к вопросу о нашей природе. «Доброго, которого хочу, то не делаю, а злое, которого не хочу, то делаю». Помните? И ничего не могу с собой поделать. У меня так получается.

 

Еще лекция Дмитрия Гусева.

Проект осуществляется с использованием гранта Президента Российской Федерации на развитие гражданского общества, предоставленного Фондом президентских грантов.

Логика. Суждение. Умозаключение контрольная по философии

ПЛАН: 1. Логика как наука……………………………………………………………..3 а) Предмет и законы логики………………………………………………………..3 б) Понятие логической формы. Логические категории и символы……………5 2. Понятие как форма мысли…………………………………………………..7 а) Понятие как форма мысли. Логическая характеристика понятий…………..7 б) Соотношение между понятиями по объему………………………………….7 в) Деление понятий. Правила и виды делений………………………………….8 г) Обобщение и ограничение понятий…………………………………………10 3. Суждение как форма мысли………………………………………………11 а) Виды и структура суждений…………………………………………………11 б) Классификация простых атрибутивных суждений по количеству и качеству……………………………………………………………………………….12 в) Распределенность терминов в простом атрибутивном суждении………….13 г) Правила вывода из суждений по логическому квадрату…………………….15 4. Умозаключение как форма мысли………………………………………..16 а) Понятие и виды умозаключений……………………………………………..16 б) Простой категорический силлогизм: правила, фигуры и модусы…………18 в) Условное и разделительно – категорическое умозаключение……………..20 г) Условно – категорическое умозаключение: правильные и неправильные модусы…………………………………………………………………………….21 д) Условно – разделительное умозаключение. Сложные и простые модусы………………………………………………………………………..…..23 е) Сокращенный силлогизм…………………………………………………….24 ж) Индуктивные умозаключения. Виды индукции…………………………..26 з) Умозаключения по аналогии………………………………………………..27 СПИСОК ЛИТЕРАТУРЫ………………………………………………….…..28 1. Логика как наука а) Предмет и законы логики Логика — это наука об общезначимых формах и средствах мысли, необходимых для рационального познания в любой области. Следовательно, предмет логики составляют: 1. Законы, которым подчиняется мышление в процессе познания объективного мира. 2. Формы мыслительного процесса — понятия, суждения и умозаключения. 3. Методы получения нового выводного знания — сходства, различия сопутствующих изменений, остатков и другие. 4. Способы доказательства истинности полученных знаний: прямое и косвенное доказательство, опровержение и так далее. Итак, логика (в наиболее широком понимании ее предмета) исследует структуру мышления, раскрывает лежащие в его основе закономерности. При этом абстрактное мышление, обобщенно, опосредствованно и активно отражая действительность, неразрывно связано с языком. Языковые выражения являются той реальностью, строение и способ употребления которой дает нам знание не только о содержании мыслей, но и об их формах, о законах мышления. Поэтому в исследовании языковых выражений и отношений между ними логика видит одну из своих основных задач. А язык в целом является при этом косвенным объектом ее внимания и интереса. Логические законы. 1) Закон тождества. Самый простой из всех логических законов – это, пожалуй, закон тождества. Он говорит: если утверждение истинно, то оно истинно, «если А, то А». Он утверждает только, что если вещь меняется, то она меняется, а если она остается одной и той же, то она остается той же. 2) Закон противоречия. организующими принципами процесса мышления, категории воспроизводят свойства и отношения бытия и познания во всеобщем и наиболее концентрированном виде. Характеристику некоторых особенностей 0 0 1 Fкатегорий можно дать, опи раясь на операцию обобщения понятий. К 0 0 1 Fкатегориям отно сятся предельно широкие по своему объему понятия, то есть те, для которых нельзя найти более широкие родовые понятия. Как 0 0 1 Fправи ло, категории являются философские понятия – «бытие», «субъект», 0 0 1 F«сущ ность», «качество», «количество», «материя», «сознание» и тому подобное. В каждой конкретной науке имеется своя система категорий. В логике к числу наиболее общих и фундаментальных понятий относятся 0 0 1 Fпо нятия логического вывода, суждения, умозаключения, индукции, 0 0 1 Fдедук ции и другие. Категории изменяются вместе с развитием нашего 0 0 1 Fпознания: обо гащается их содержание, изменяются взаимосвязи между категориями, меняется их состав и тому подобное. Символ (от греч. symbolon – 0 01 Fзнак, опознавательная приме та) — идея, образ или объект, имеющий собственное содержание и одновременно 0 0 1 Fпредставляющий в обобщенной, неразвернутой фор ме некоторое иное содержание. Символ стоит между (чистым) знаком, у которого собственное содержание ничтожно, и моделью, имеющей прямое сходство с моделируемым объектом, что позволяет модели замещать последний в процессе исследования. Символ используется человеком в некоторых видах деятельности и имеет в силу этого определенную цель. Он всегда служит 0 0 1 Fобнару жению чего-то неявного, не лежащего на поверхности, 0 0 1 Fнепредска зуемого. Если цель отсутствует, то нет и символа как элемента социальной жизни, а есть то, что обычно называется знаком и служит для простого обозначения объекта. Роль символа в человеческой практике и познании мира невозможно переоценить. Разъяснение смысла символа неизбежно ведет к новым символам; которые не только не способны исчерпать всю его глубину, но и сами требуют разъяснения. 2. Понятие как форма мысли а) Понятие как форма мысли. Логическая характеристика понятий Понятие как форма мышления отражает предметы и их совокупность в абстрактной, обобщенной форме на основании их существенных признаков. Понятие – одна из основных форм научного познания. Формируя понятие, наука отражает в них изучаемые ею предметы, явления, процессы. Кроме единичных (индивидуальных) и общих признаков логика выделяет признаки существенные и несущественные. Признаки, необходимо принадлежащие предмету, выражающие его сущность, называют существенными. Они могут быть общими и единичными. Понятия, отражающие множество предметов, включают общие существенные признаки (напр. способность создавать орудие труда). Понятие, отражающее один предмет (напр. «Аристотель»), наряду с общими существенными признаками (человек, древнегреческий философ) включает единичные признаки. Признаки, которые могут принадлежать, но могут и не принадлежать предмету и которые не выражают его сущность, называются несущественными. Понятие качественно отличается от форм чувственного познания: ощущений, восприятия и представлений, существующих в сознание человека в виде наглядных образов отдельных предметов или их свойств. Восприятие и представление – это чувственно-наглядный образ какого-либо конкретного предмета. Понятие лишено наглядности. Отражая существенное, понятия не содержат всего богатства индивидуальных признаков предмета и в этом смысле они беднее форм чувственного познания – восприятия и представления. Вместе с тем, они позволяют глубже проникнуть в действительность, отобразить её с большей полнотой, на что не способно чувственное познание. б) Соотношение между понятиями по объему Предмет, о котором известно только то, что он подходит под то или иное понятие, и больше ничего, есть целиком мыслительное образование и называется абстрактным предметом. Совокупность абстрактных предметов, 0 0 1 Fсоответ ствующих одному и тому же понятию, составляет его объем. Множество предметов, 0 01 F которое мыслится в понятии, называ ется объемом понятия. Объем понятия, составляют все другие понятия, для которых оно является общим. Например, понятие машины является общим для таких понятий, как автомобиль, грейдер, экскаватор и так далее. Такой объем можно 0 0 1 Fбыло бы назвать объе мом разнообразия, потому что он показывает, как 0 0 1 Fвелико число разно видностей данного явления, как разнообразно оно: объем понятия – все предметы, к которым относится данное понятие. Объём понятия не может состоять из реальных предметов, а может состоять лишь из мыслей. объем понятия составляют утверждения о наличии 0 0 1 F(существовании) конкретных пред метов (или их категорий, понимаемых как одно целое), которые обладают свойствами, подходящими под данное понятие, что позволяет быть реальным и данному понятию. Объемы, составленные из утверждений о существовании предметов, соответствующих данному понятию; могут быть названы количественными. При обращении с объемами понятий возможна следующая ошибка: части предмета могут полагаться частями объёма. Получается сколько у предмета частей, таков и его объем. Но части предмета – это не экземпляры, 0 0 1 Fне категории и разновидности предмета. Плавник не есть разновид ность рыбы, потому объемы этих двух понятий не соприкасаются. г) Обобщение и ограничение понятий Обобщить понятие — значит, перейти от понятия с меньшим объемом, но с большим содержанием к понятию с большим объемом, но с меньшим содержанием. Обобщение понятия не может быть беспредельным. Наиболее общими являются понятия с предельно широким объемом – 0 01 F кате гории, например «материя», «сознание, «отношение» и тому подобное. Категории не имеют 0 0 1 Fродового понятия, обоб щить их нельзя. Ограничение понятия представляет собой операцию, 0 0 1 Fпротивопо ложенную операции обобщения. Ограничить понятие — значит, перейти от понятия с большим объемом, но с меньшим содержанием к понятию с меньшим объемом, но большим содержанием. 0 0 1 F Пределом ограничения по нятия является единичное понятие. Таким образом, изменяя объем исходного понятия, мы изменяем и его содержание, осуществляя тем самым переход к новому понятию – с большим объемом и меньшим содержанием (обобщение) или меньшим объемом и большим содержанием (ограничение). 0 0 1 FЛогические операции обобщения и ограничения понятий широ ко применяются в практике мышления: переходя от понятий одного объема к понятиям другого объема, мы уточняем предмет нашей мысли, делаем наше 0 0 1 Fмышление более определенным и последова тельным. 0 0 1 FОбобщение и ограничение поня тий не следует смешивать с 0 0 1 Fмыслен ным переходом от части к целому и выделением части из целого. 0 0 1 FНапри мер, сутки делятся на часы, часы на минуты, минуты на секунды. 0 0 1 FКаждое последующее понятие не явля ется видом предыдущего, которое в 0 0 1 Fсвою очередь нельзя рассматри вать как родовое. Поэтому переход от понятия «час» к понятию «сутки» – не обобщение, а переход от части к целому; переход от понятия «час» к понятию «минута» – не ограничение, а выделение части из целого. 3. Суждение как форма мысли а) Виды и структура суждений Виды простых суждений, которые классифицируются по следующим основаниям. 1. По объему субъекта (по количеству). Единичные — суждения, включающие утверждение или отрицание об одном предмете. Формула такого суждения: Это S есть (не есть) P. Частные суждения, в которых что-либо утверждается или отрицается о части предметов некоторого класса. Эта часть может быть неопределенной и определенной. В зависимости от данного обстоятельства частные суждения подразделяются на неопределенные и определенные. В неопределенных суждениях логическая схема такова: «Некоторые 8 есть Р». Слово «некоторые» придает им неопределенность. Определенное частное суждение содержит знание и о той, и о другой части субъекта суждения. Оно имеет такую логическую схему: «Только некоторые S есть Р». Общие — суждения, в которых что-либо утверждается или отрицается в каждом предмете данного класса. Логическая схема таких суждений имеет вид: «Все S есть Р» или «Ни одно S не есть Р» 2. По качеству связки суждения могут быть утвердительные или отрицательные. Следует различать отрицательное суждение и негативную форму выражения утвердительного суждения. Такого вида суждения не всегда идентичны. 3. По содержанию предиката суждения делятся на суждения свойства (атрибутивные), суждения отношения (релятивные) и суждения существования (экзистенциальные). Суждение I (Некоторые S суть Р). «Некоторые студенты нашей группы (S 0 01 F) – отличники (Р)». Субъект этого суждения не распре делен, так как в нем 0 0 1 Fмыслится только часть студентов нашей груп пы, объем субъекта лишь частично включается в объем предиката. Но и объем предиката лишь частично включается в объем субъекта: не все, а только некоторые отличники – студенты нашей группы. Следовательно, в частноутвердительном суждении ни S, ни Р не распределены. Суждение О (некоторые S не суть Р). «Некоторые студенты нашей группы (S) – не отличники (Р)». Субъект этого суждения не распределен, 0 0 1 Fпре дикат распределен, в нем мыслятся все отличники, ни один из 0 0 1 Fкото рых не включается в ту часть студентов нашей группы, которая мыслится в 0 0 1 Fсубъекте. Следовательно, в частноотрицательном сужде нии S не распределен, а Р распределен. г) Правила вывода из суждений по логическому квадрату Несравнимыми среди простых являются суждения, имеющие различные субъекты или предикаты. Таковы, например, два суждения: «Среди космонавтов есть летчики»; «Среди космонавтов есть женщины». Сравнимыми являются суждения с одинаковыми субъектами и предикатами и различающиеся связкой или квантором. Обычно их называют 0 0 1 Fсуждениями одинаковой материи. Например: «Все амери канские индейцы живут в резервациях»; «Некоторые американские индейцы не живут в резервациях». 0 0 1 FОтношения между простыми суждениями обычно рассматрива ются с помощью мнемонической схемы, называемой логическим квадратом. Его 0 0 1 Fвершины символизируют простые катего рические суждения – А, Е, I, О; стороны и диагонали – отношения между суждениями. Противоположность (контрарность) Частичная совместимость (субконтрарность) Противоречие (контрадикторность) Среди сравнимых различают совместимые и несовместимые суждения. К совместимым относятся суждения, которые одновременно могут быть истинными. Различают три вида совместимости: 1) 0 01 Fэк вивалентность (полная совместимость), 2) 0 01 Fчастичная совмести мость (субконтрарность) и 3) подчинение. 1. Эквивалентными являются такие суждения, которые имеют одинаковые логические характеристики: 0 01 F одинаковые субъ екты и 0 0 1 Fпредикаты, однотипную – утвердительную или отрицатель ную – связку, одну и ту же выраженную квантором количественную характеристику. С помощью логического квадрата отношения между простыми эквивалентными суждениями не иллюстрируются. 2. Частичная совместимость характерна для суждений I u О, которые могут быть одновременно истинными, но не могут быть одновременно ложными. 3. Подчинение имеет место между суждениями А и I, Е и О. Для них характерны следующие две зависимости. 0 0 1 FПри истинности общего суждения частное всегда будет истин ным При ложности частного суждения общее суждение также будет ложным Отношение несовместимости. Несовместимыми являются суждения А и Е, А и О, Е и I, которые одновременно не могут быть истинными. Различают два вида несовместимости: противоположность и противоречие. 1. Противоположными (контрарными) являются суждения А и Е, которые одновременно не могут быть истинными, но могут быть одновременно ложными. 2. 0 01 FПротиворечащими (контрадикторными) являются сужде ния А и О, Е и I, 0 01 Fкоторые одновременно не могут быть ни истин ными, ни ложными. Hесовместимые единичные суждения могут находиться лишь в отношении противоречия и не могут находиться в отношении противоположности, 0 01 F ибо каждому от дельному предмету может быть либо 0 0 1 Fприсущ, либо не присущ оп ределенный признак. Сказуемое P (предикат) – то, что мы высказываем (3 вида суждений): • Повествовательные – это суждение относительно событий, состояний, процессов или деятельности скоропроходящих. Прим: «Роза в саду цветет». • Описательные – когда одному или многим предметам приписывается какое-нибудь свойство. Субъектом всегда является определенная вещь. Пример: «Огонь горяч», «снег бел». Отношение между подлежащим и сказуемым: 1. Суждения тождества – понятия субъекта и предиката имеют один и тот же объем. Прим: «всякий равносторонний треугольник есть равноугольный треугольник» 2. Суждения подчинения – понятия с менее широким объемом подчиняется понятию с более широким объемом. Прим: «Собака есть домашнее животное» 3. Суждения отношения — именно пространства, времени, отношения. Прим: «Дом находится на улице» Фигурами силлогизма называются формы силлогизма, отличающиеся расположением среднего термина в посылках: Фигура 1 Фигура 2 Фигура 3 Фигура 4 0 3 0 1Большая посылка: M–P P–M M–P P–M Меньшая посылка: S–M S–M M–S M–S Заключение: S–P S–P S–P S–P Каждой фигуре отвечают модусы – формы силлогизма, различающиеся количеством и качеством посылок и заключения. Модусы изучались ещё средневековыми школами, и для правильных модусов каждой фигуры были придуманы мнемонические имена: Фигура 1 Фигура 2 Фигура 3 Фигура 4 Barbara Cesare Darapti Bramantip Celarent Camestre s Disamis Camenes Darii Festino Datisi Dimaris Ferio Baroco Felapton Fesapo Bocardo Fresison Ferison в) Условное и разделительно – категорическое умозаключение 0 0 1 FЧисто условным называется умозаключение, обе посылки кото рого являются условными суждениями. (q -> г) р->г 0 0 1 FВывод в чисто условном умозаключении основывается на прави ле: следствие следствия есть следствие основания. 0 0 1 FУмозаключение, в котором заключение получается из двух услов ных 0 0 1 Fпосылок, относится к простым. Однако заключение может сле довать из 0 0 1 Fбольшего числа посылок, которые образуют цепь услов ных суждений. Такие умозаключения называются сложными. 0 0 1 FУсловно-категорическим называется умозаключение, в кото ром одна из посылок –условное, а другая посылка и заключение – категорические суждения. 0 0 1 FЭто умозаключение имеет два правильных модуса: 1) утверждаю щий и 2) отрицающий. 1. В утверждающем модусе 0 01 F посылка, выражен ная категорическим суждением, утверждает истинность основания условной посылки, а заключение утверждает истинность следствия; рассуждение направлено от утверждения истинности основания к утверждению истинности следствия. 2. В отрицающем модусе посылка, выраженная категорическим 0 0 1 Fсуждением, отрицает истинность следствия услов ной посылки, а 0 0 1 Fзаключение отрицает истинность основания. Рассуж дение направлено от 0 0 1 Fотрицания истинности следствия к отрица нию истинности основания. 0 0 1 FИз четырех модусов условно-категорического умозаключе ния, 0 0 1 Fисчерпывающих все возможные комбинации посылок, досто верные заключения дают два: утверждающий (modus ponens) (1) и отрицающий (modus tollens) (2). Они выражают законы логики и называются правильными 0 0 1 Fмодусами условно-категорического умо заключения. Эти модусы подчиняются правилу: 0 01 Fутверждение осно вания ведет к утверждению следствия и отрицание следствия – к отрицанию основания. Два других модуса (3 и 4) достоверных заключений не дают. Они называются неправильными модусами и подчиняются правилу: отрицание основания не 0 0 1 Fведет с необходи мостью к отрицанию следствия и утверждение следствия не ведет с необходимостью к утверждению основания. г) Условно – категорическое умозаключение: правильные и неправильные модусы Формула ((а — Ь) л Ь) -» а (3) не является законом логики. Она означает, что нельзя достоверно умозаключить от утверждения следствия к утверждению основания. Люди иногда неправильно умозаключают так: Если бухта замерзла, то суда не могут входить в бухту. Суда не могут входить в бухту. Бухта замерзла. Заключение будет лишь вероятностным суждением, то есть вероятно, что бухта замерзла, но возможно и то, что дует сильный ветер, или бухта заминирована, или существует другая причина, по которой суда не могут входить в бухту. Вероятностное заключение получится и в таком умозаключении: Если данное тело – графит, то оно электропроводно. Данное тело электропроводно. Вероятно, данное тело – графит. Второй вероятностный модус. Это второй модус, не дающий достоверного заключения. Структура его: Если а, то Ь. Не-а._____ Вероятно, не-Ь. Схема: а -» Ь ~а Вероятно, Ъ Формула ((а -» Ь) л a) -» b (4) не является законом логики. Она означает, что нельзя принимать заключение за достоверное, умозаключая от отрицания основания к отрицанию следствия.Некоторые врачи ошибочно рассуждают так: Если человек имеет повышенную температуру, то он болен. Данный человек не имеет повышенной температуры.(r->s),1qv1s 1pv1r е) Сокращенный силлогизм Силлогизм, в котором выражены все его части – обе посылки и 0 0 1 Fзаключение, называется полным. Однако на практике чаще использу ются силлогизмы, в которых одна из посылок или заключение явно не выражаются, а подразумеваются. 0 0 1 FСиллогизм с пропущенной посылкой или заключением называет ся сокращенным силлогизмом, или энтимемой. Энтимема в переводе с греческого буквально означает «в уме». Широко 0 0 1 Fиспользуются энтимемы простого категорического сил логизма, особенно 0 0 1 Fвыводы по первой фигуре. Например: «Н. совер шил преступление и поэтому подлежит уголовной ответственности». Здесь пропущена большая 0 0 1 Fпосылка: «Лицо, совершившее преступ ление, подлежит уголовной ответственности». Она представляет собой общеизвестное положение, 0 0 1 Fформулировать которое необяза тельно. Полный силлогизм строится по 1-й фигуре: Лицо, совершившее преступление (М), подлежит уголовной ответственности (р) Н. (s) совершил преступление (М) Н. (s) подлежит уголовной ответственности (р) В зависимости от того, какая часть силлогизма пропущена, 0 01 Fразли чают три вида энтимемы: с пропущенной большей посылкой, с 0 01 Fпро пущенной меньшей посылкой и с пропущенным заключением. Умозаключение в форме энтимемы может быть построено и по 2-й фигуре; по 3-й фигуре оно строится редко. Форму энтимемы принимают также умозаключения, посылками которых являются условные и разделительные суждения. 0 0 1 FУсловно-категорический силлогизм с пропущенной большей по сылкой: 0 0 1 F«Уголовное дело не может быть возбуждено, так как собы тие преступления не имело места». Здесь пропущена большая посылка – условное суждение «Если событие преступления не имело места, то уголовное дело не может быть возбуждено». Она содержит известное положение Уголовно-процессуального кодекса, которое подразумевается. Разделительно-категорический силлогизм с опущенной большей посылкой: 0 01 F «По данному делу не может быть вынесен оправдатель ный приговор, он должен быть обвинительным». Большая посылка – разделительное суждение «По данному делу может быть вынесен либо оправдательный, либо обвинительный приговор» не формулируется. 0 0 1 FРазделительно-категорический силлогизм с опущенным заклю чением: «Смерть произошла либо в результате убийства, либо в результате самоубийства, либо в результате несчастного случая, либо в силу естественных причин. Смерть произошла в результате несчастного случая». Заключение, отрицающее все другие альтернативы, обычно не формулируется. Использование сокращенных силлогизмов обусловлено тем, что пропущенная посылка или заключение либо содержит известное положение, 0 0 1 Fкоторое не нуждается в устном или письменном выраже нии, либо в контексте выраженных частей умозаключения она легко подразумевается. 0 0 1 FИменно поэтому рассуждение протекает, как пра вило, в форме энтимем. Но, поскольку в энтимеме выражены не все части умозаключения, скрывающуюся в ней ошибку обнаружить труднее, чем в полном 0 0 1 Fумозаключении. Поэтому для проверки пра вильности рассуждения следует 0 0 1 Fнайти пропущенные части умозак лючения и восстановить энтимему в полный силлогизм. ж) Индуктивные умозаключения. Виды индукции Индукция — это умозаключение, в результате которого на основе знания об отдельных предметах какого-либо класса делается вывод обо всем классе этих предметов. Наблюдение природных явлений и обобщение полученных результатов представляют собой один из самых распространенных методов постижения окружающего мира. Факты наталкивают человека на общие закономерности, наводят на них. Поэтому Аристотель называл этот вид умозаключения наведением. Индукцию принято подразделять на полную и неполную; последняя в свою очередь распадается еще на две разновидности. Кроме того, имеется также научная индукция. Самой простой разновидностью индуктивного процесса является полная индукция. В этом случае перечисляются все без исключения предметы данного класса. Заключение суммирует итог. С полной индукцией весьма часто приходится сталкиваться в повседневной практической деятельности. Мы можем делать обобщающие выводы о цене на разнообразные товары такого-то предприятия, о морозных днях на прошлой неделе, об этажности зданий в данном квартале. Неполная индукция. В научном познании возможность исчерпывающим образом охватить все изучаемые явления данного класса встречается сравнительно редко. Более распространены обобщения, построенные на основе знания только части

Урок 6. Умозаключения

В этом уроке мы, наконец, переходим к теме, которая составляет ядро любого рассуждения и любой логической системы – умозаключениям. В четвёртом уроке мы говорили, что рассуждение – это совокупность суждений или высказываний. Очевидно, что такое определение не полно, ведь оно ничего не говорит о том, почему вдруг какие-то разные высказывания оказались рядом. Если дать более точное определение, то рассуждение – это процесс обоснования какого-либо высказывания с помощью его последовательного вывода из других высказываний. Этот вывод чаще всего осуществляется в форме умозаключений.

Содержание:

Умозаключение – это непосредственный переход от одного или нескольких высказываний А₁, А₂, …, А_n к высказыванию В. А₁, А₂, …, А_n называют посылками. Посылка может быть одна, их может быть две, три, четыре, в принципе – сколько угодно. В посылках содержится известная нам информация. В – это заключение. В заключении находится уже новая информация, которую мы извлекли из посылок с помощью специальных процедур. Эта новая информация уже содержалась в посылках, но в скрытом виде. Так вот задача умозаключения сделать это скрытое явным. Кроме того, иногда посылки называют аргументами, а заключение – тезисом, а само умозаключение в этом случае называют обоснованием. Разница между умозаключением и обоснованием состоит в том, что в первом случае, мы не знаем, к какому заключению мы придём, а во втором – тезис нам уже известен, мы просто хотим установить его связь с посылками-аргументами.

В качестве иллюстрации умозаключения можно взять рассуждения Эркюля Пуаро из «Убийства в восточном экспрессе» Агаты Кристи:

Перебрав в уме еще раз показания пассажиров, я пришел к весьма любопытным результатам. Для начала возьмем показания мистера Маккуина. Первая беседа с ним не вызвала у меня никаких подозрений. Но во время второй он обронил небезынтересную фразу. Я сообщил ему, что мы нашли записку, в которой упоминается о деле Армстронгов. Он сказал: «А разве…» – осекся и, помолчав, добавил: «Ну это самое… неужели старик поступил так опрометчиво?…»

Но я почувствовал, что он перестроился на ходу. Предположим, он хотел сказать: «А разве ее не сожгли?» Следовательно, Маккуин знал и о записке, и о том, что ее сожгли, или, говоря другими словами, он был убийцей или пособником убийцы.

Логики записывают умозаключения следующим образом:

Над чертой располагаются посылки, под чертой – заключение, а сама черта обозначает отношение логического следования.

Критерии истинности умозаключений

Также как и для суждений, для умозаключений существуют определённые условия их истинности. При определении, истинное умозаключение или ложное, нужно обращать внимание на два аспекта. Первый аспект – это истинность посылок. Если хотя бы одна из посылок ложна, то и сделанное заключение тоже будет ложным. Поскольку заключение – это та информация, которая была скрыта в посылках и которую мы просто извлекли на свет, то из неверных посылок невозможно случайно получить верный вывод. Это можно сравнить с попыткой сделать бифштекс из моркови. Наверное, моркови можно придать цвет и форму бифштекса, но внутри всё равно будет морковь, а не мясо. Никакие кулинарные операции не преобразуют одно в другое.

Второй аспект – это правильность самого умозаключения с точки зрения его логической формы. Дело в том, что истинность посылок – это важное, но недостаточное условие для того, чтобы заключение было правильным. Нередки ситуации, когда посылки истинны, но заключение неверно. В качестве примера неправильного умозаключения при истинности посылок можно привести умозаключение голубки из «Алисы в стране чудес» Кэрролла. Голубка обвиняет Алису, в том, что она не змея. Вот как она приходит к этому выводу:

Змеи едят яйца.
Девочки едят яйца.
Значит, девочки – это змеи.

Хотя посылки правильные, заключение абсурдно. Умозаключение в целом сделано неверно. Чтобы избежать подобных ошибок, логики выявили такие умозаключения, логические формы которых при истинности посылок гарантируют истинность заключения. Их принято называть правильными умозаключениями. Таким образом, чтобы умозаключение было сделано верно, нужно следить за истинностью посылок и за правильностью самой формы умозаключения.

Мы рассмотрим различные формы правильных умозаключений на примере силлогистики. В этом уроке мы разберём самые простые однопосылочные заключения. В следующем уроке – более сложные заключения: силлогизмы, энтимемы, многопосылочные заключения.

Умозаключения по логическому квадрату

Чтобы было легче запомнить, какие именно типы умозаключений возможны между категорическими атрибутивными высказываниями, логики придумали специальный логический квадрат, изображающий отношения между ними. Поэтому некоторые однопосылочные умозаключения также называют умозаключениями по логическому квадрату. Посмотрим на этот квадрат:

Начнём с отношений подчинения. Мы уже сталкивались с ними в четвёртом уроке, когда рассматривали условия истинности для частно-утвердительных и частно-отрицательных высказываний. Мы говорили, что из высказывания «Все S есть P» будет логичным вывести высказывание «Некоторые S есть P», а из высказывания «Ни один S не есть P» – «Некоторые S не есть P». Таким образом, возможны следующие типы умозаключений:

• Все S есть P
• Некоторые S есть P
• Все птицы имеют клюв. Следовательно, некоторые птицы имеют клюв.
• Ни один S не есть P
• Некоторые S не есть P
• Ни один гусь не хочет быть пойман и зажарен. Следовательно, некоторые гуси не хотят быть пойманными и зажаренными.

Кроме того, по правилу контрапозиции из отношений подчинения можно вывести ещё два правильных умозаключения. Правило контрапозиции – это логический закон, который гласит: если из высказывания А следует высказывание В, то из высказывания «неверно, что В» будет следовать высказывание «неверно, что А». Вы можете попробовать проверить этот закон с помощью таблицы истинности. Итак, будут верны и следующие умозаключения по контрапозиции:

• Неверно, что некоторые S есть P
• Неверно, что все S есть P
• Неверно, что некоторые автомобили не имеют колёс. Поэтому неверно, что все автомобили не имеют колёс.
• Неверно, что некоторые S не есть P
• Неверно, что все S не есть P
• Неверно, что некоторые вина не являются спиртными напитками. Таким образом, неверно, что все вина не являются спиртными напитками.

Отношение контрарности (противоположности) означает, что высказывания типа «Все S есть P» и «Ни один S не есть P» не могут быть одновременно истинными, но они могут быть одновременно ложными. Это хорошо видно из таблицы истинности для категоричных атрибутивных высказываний, которую мы построили в прошлом уроке. Отсюда можно вывести так называемый закон контрарного противоречия: Неверно, что все S есть P и в то же время ни один S не есть P.

По закону контрарного противоречия будут истинными следующие виды умозаключений:

• Все S есть P
• Неверно, что ни один S не есть P
• Все яблоки – это фрукты. Следовательно, неверно, что ни одно яблоко не является фруктом.
• Ни один S не есть P
• Неверно, что все S есть P
• Ни один кит не умеет летать. Поэтому неверно, что все киты умеют летать.

Отношения субконтрарности (подпротивоположности) означают, что высказывания типа «Некоторые S есть P» и «Некоторые S не есть P» не могут быть одновременно ложными, хотя могут быть одновременно истинными. На этом основании может быть сформулирован закон субконтрарного исключённого третьего: Некоторые S не есть P или Некоторые S есть P.

• Согласно этому закону правильными будут следующие умозаключения:
• Неверно, что некоторые S есть P
• Некоторые S не есть P
• Неверно, что некоторые продукты полезны для здоровья. Поэтому некоторые продукты не полезны для здоровья.
• Неверно, что некоторые S не есть P
• Некоторые S есть P
• Неверно, что некоторые ученики из нашего класса не являются двоечниками. Таким образом, некоторые ученики из нашего класса являются двоечниками.

Отношения противоречия (контрадикторности) говорят о том, что высказывания, находящиеся в них, не могут быть одновременно истинными или ложными. На основании этих отношений можно сформулировать два закона противоречия и два закона исключённого третьего. Первый закон противоречия: Неверно, что все S есть P и некоторые S не есть P. Второй закон противоречия: Неверно, что ни один S не есть P и некоторые S есть P. Первый закон исключённого третьего: Все S есть P или некоторые S не есть P. Второй закон исключённого третьего: Ни один S не есть P или некоторые S есть P.

На этих законах строятся умозаключения следующих видов:

• Все S есть P
• Неверно, что некоторые S не есть P
• Все дети нуждаются в заботе. Следовательно, неверно, что некоторые дети не нуждаются в заботе.
• Некоторые S не есть P
• Неверно, что все S есть P
• Некоторые книги не являются скучными. Поэтому, неверно, что все книги являются скучными.
• Неверно, что все S есть P
• Некоторые S не есть P
• Неверно, что все сотрудники нашей фирмы усердно работают. Таким образом, некоторые сотрудники нашей фирмы не работают усердно.
• Неверно, что некоторые S не есть P
• Все S есть P
• Неверно, что некоторые зебры не имеют полосок на коже. Следовательно, все зебры имеют полоски на коже.
• Ни один S не есть P
• Неверно, что некоторые S есть P
• Ни одна картина в этом зале не относится к XX веку. Поэтому неверно, что некоторые картины в этом зале относятся к XX веку.
• Некоторые S есть P
• Неверно, что ни один S не есть P
• Некоторые студенты занимаются спортом. Таким образом, неверно, что ни один студент не занимается спортом.
• Неверно, что ни один S не есть P
• Некоторые S есть P
• Неверно, что ни один учёный не интересуется искусством. Следовательно, некоторые учёные интересуются искусством.
• Неверно, что некоторые S есть P
• Ни один S не есть P
• Неверно, что некоторые коты курят сигары. Таким образом, ни один кот не курит сигары.

Как вы, скорее всего, заметили во всех этих умозаключениях, высказывания над чертой и под чертой несут одну и ту же информацию, просто поданную в разной форме. Важная деталь заключается в том, что смысл одних из этих высказываний воспринимается легко и интуитивно, в то время как смысл других тёмен, и над ними порой приходится поломать голову. Например, смысл утвердительных высказываний воспринимается легче, чем смысл отрицательных высказываний, смысл высказываний с одним отрицанием более понятен, чем смысл высказываний с двумя отрицаниями. Таким образом, основное назначение умозаключений по логическому квадрату состоит в том, чтобы привести сложные для восприятия, непонятные высказывания к наиболее простой и ясной форме.

Операция обращения

Ещё одним видом однопосылочных умозаключений является обращение. Это такой тип умозаключений, при которых субъект посылки совпадает с предикатом заключения, а субъект заключения совпадает с предикатом посылки. Грубо говоря, в заключении S и P просто меняются местами.

Прежде чем перейти к умозаключениям через обращение, построим таблицу истинности для высказываний, в которых P встанет на место субъекта, а S – на место предиката.

Сравните её с той таблицей, которую мы строили в прошлом уроке. Обращение, как и другие умозаключения, может быть правильным, только когда посылка и заключение одновременно истинны. При сравнении двух таблиц, вы увидите, что таких комбинаций не так уж и много.

Итак, существует два вида обращения: чистое и с ограничением. Чистое обращение происходит тогда, когда количественная характеристика не изменяется, то есть если в посылке было слово «все», то и в заключении тоже будет слова «все»/«ни один», если в посылке слово «некоторые», то и в заключении «некоторые. Соответственно, при обращении с ограничением количественная характеристика меняется: были «все», а стали «некоторые». Для высказываний типа «Ни один S не есть P» и «Некоторые S есть P» правильным будет следующее чистое обращение:

• Ни один S не есть P
• Ни один P не есть S
• Ни один человек не может выжить без воздуха. Следовательно, ни одно живое существо, способное выжить без воздуха, не является человеком.
• Некоторые S есть P
• Некоторые P есть S
• Некоторые змеи ядовиты. Поэтому, некоторые ядовитые существа – это змеи.
• Для высказываний типа «Все S есть P» и «Ни один S не есть P» верно обращение с ограничением:
• Все S есть P
• Некоторые P есть S
• Все пингвины – это птицы. Таким образом, некоторые птицы – это пингвины.
• Ни один S не есть P
• Некоторый P не есть S
• Ни один крокодил не ест зефир. Следовательно, некоторые существа, едящие зефир, не являются крокодилами.
• Высказывания типа «Некоторые S не есть P» вообще не обращаются.

Хотя обращения, как и умозаключения по логическому квадрату, это однопосылочные умозаключения, и мы точно также извлекаем всю новую информацию из имеющейся посылки, посылку и заключение в них уже нельзя назвать просто разными формулировками одной и той же информации. Полученная информация относится уже к другому субъекту, а потому она уже не кажется такой тривиальной.

Итак, в этом уроке мы начали рассматривать правильные виды умозаключений. Мы поговорили о самых простейших однопосылочных умозаключениях: умозаключениях по логическому квадрату и умозаключениях через обращение. Хотя эти умозаключения довольно просты и даже где-то тривиальны, люди повсеместно совершают в них ошибки. Понятно, что сложно удержать в памяти все виды правильных умозаключений, поэтому, когда вы будете выполнять упражнения или столкнётесь с необходимостью проверить или сделать однопосылочное умозаключение в реальной жизни, не бойтесь прибегать к помощи модельных схем и таблиц истинности. Они помогут вам проверить, всегда ли при истинности посылок заключение тоже истинное, а это главное для правильного умозаключения.

Упражнение «Подберите ключ»

В этой игре вам нужно создать ключ правильной формы. Для этого установите засечки нужной длины (от 1 до 3, 0 – быть не может), а затем нажмите кнопку «Попробовать». Вам будут даны 2 суждения, сколько засечек выбранной длины присутствуют в ключе (для простоты значение «наличие»), и сколько из выбранных находятся на своём месте (для простоты значение «на месте»). Скорректируйте своё решение и пробуйте, пока не подберёте ключ.

Упражнения

1

Сделайте все возможные умозаключения из следующих высказываний по логическому квадрату:

• Все медведи на зиму залегают в спячку.
• Неверно, что все люди завистливы.
• Ни один гном не достигает роста в два метра.
• Неверно, что ни один человек не был на Северном полюсе.
• Некоторые люди никогда не видели снега.
• Некоторые автобусы ходят по расписанию.
• Неверно, что некоторые слоны летали на луну.
• Неверно, что некоторые птицы не имеют крыльев.

2

Сделайте обращения с теми, высказываниями, с которыми это возможно:

• Никто ещё не построил машину времени.
• Некоторые официанты очень назойливы.
• Все профессионалы опытны в своём деле.
• Некоторые книги не имеют твёрдой обложки.

3

Проверьте, правильно ли сделаны следующие умозаключения:

• Некоторые кролики не носят белые перчатки. Следовательно, некоторые кролики носят белые перчатки.
• Неверно, что никто не был на Луне. Таким образом, некоторые люди были на Луне.
• Все люди смертны. Поэтому все смертные – это люди.
• Некоторые птицы не умеют летать. Следовательно, некоторые существа, не умеющие летать, это птицы.
• Ни один ягнёнок не имеет пристрастия к виски. Следовательно, ни одно существо, имеющее пристрастие к виски, не является ягнёнком.
• Некоторые морские животные млекопитающие. Таким образом, неверно, что ни одно морское животное не является млекопитающим.

Проверьте свои знания

Если вы хотите проверить свои знания по теме данного урока, можете пройти небольшой тест, состоящий из нескольких вопросов. В каждом вопросе правильным может быть только 1 вариант. После выбора вами одного из вариантов, система автоматически переходит к следующему вопросу. На получаемые вами баллы влияет правильность ваших ответов и затраченное на прохождение время. Обратите внимание, что вопросы каждый раз разные, а варианты перемешиваются.

Ксения Галанина

Факт, вывод, суждение

FIJ выглядит простой темой, но часто заставляет студентов совершать ошибки. Давайте посмотрим на определения FIJ и связанных с ними понятий.

Факт: Факты, которые имеют дело с частями информации, которые человек слышал, видел или читал и которые открыты для обнаружения или проверки.

Также факт — это что-то продемонстрированное или известное о существовании. Формулировка здесь очень важна. Факт — это часть информации, которая известна людям, но может не соответствовать действительности.Например, «Солнце вращается вокруг Земли» было фактом в то время, но не сейчас.

Суждение: Суждение, то есть мнения, которые подразумевают одобрение или неодобрение людей, объектов, ситуаций и событий в прошлом, настоящем или будущем.

Итак, суждения бывают личными и субъективными. Следующая информация полезна при классификации суждений

1. Утверждение, которое подразумевает «одобрение» или «неодобрение»

Какой великолепный вид !,

2.Заявления о том, что «навязать принуждение» должны или должны

Вам следует работать усерднее

3. Заявление о том, что «сравнивайте» неизмеримые вещи

Он лучший мальчик в классе

4. Утверждения изменяют характер атрибутов.

Вы бежите очень медленно

5. Прогнозирование с использованием воли или воли

Я стану капитаном команды

6. Пословицы и максимы, которые не являются универсальными истинами

Честность — это самое главное. лучшая политика (как мы проверяем?)

Вывод: Выводы, которые представляют собой выводы о неизвестном на основе известного.

1. Результаты предпринятых действий или произошедшего инцидента.

С тех пор, как мост рухнул, жители деревни столкнулись с большой проблемой добраться до города.

2. Ожидания или возможности того, что что-то произойдет в результате чего-то другого.

Если произойдет землетрясение, погибнут люди

3. Любая пословица, действующая на причинно-следственную связь

Яблоко в день удерживает доктора

Как ответить на эти вопросы: Суждения можно определить, наблюдая за тоном предложения вместе с ключевыми словами, описанными выше.Если заявление было сделано отдельным лицом и составлено лично, может быть не принято другими, то это приговор. Утверждение — это факт, который можно проверить «чувствами». В противном случае это приговор. Если суждение основано на каких-то фактах, то это умозаключение.

Давайте посмотрим на несколько примеров:

Пример — 1

1. Кажется, что большая часть нашего повседневного внимания сосредоточена на выполнении задач, пробираться через жизненные задачи — это может казаться беговой дорожкой, которая ни к чему не приведет;
где детская радость?
2.Мы не делаем того, что делает нас счастливыми; то, что приносит нам радость; то, что нам не терпится сделать, потому что нам это очень нравится.
3. Это то, из чего состоит радостная жизнь — определение своего призвания и искренняя приверженность ему.
4. Когда это происходит, каждый момент становится вашим праздником; это прилив энергии
, который приходит с чувством полного погружения в то, что вы любите больше всего.
(1) IIIJ
(2) IFIJ
(3) JFJJ
(4) JJJJ
(5) JFII

1.Кажется, что большая часть нашего повседневного внимания сосредоточена на выполнении задач, на продвижении нашего
через жизненные задачи — это может показаться беговой дорожкой, которая никуда не приведет;
где детская радость?

В заявлении 1 говорится: «Это похоже на беговую дорожку, которая ни к чему не приведет». Это личная точка зрения. так суждение.

2. Мы не делаем того, что делает нас счастливыми; то, что приносит нам радость; то, что нам не терпится сделать, потому что нам это очень нравится.
Утверждение 2 — это личная точка зрения, которую не обязательно разделяют многие. Это приговор.

3. Это то, из чего состоит радостная жизнь — определение своего призвания и искренняя приверженность ему.

Утверждение 3 — это мнение, которое нельзя проверить или испытать на собственном опыте. Это приговор.

4. Когда это происходит, каждый момент становится вашим праздником; это прилив энергии
, который приходит с чувством полного погружения в то, что вы любите больше всего.

Утверждение 4 — это чья-то личная оценка собственного опыта. Это невозможно проверить. Это тоже приговор.
Следовательно, правильный ответ — вариант 4.

Пример — 2

1. Учитывая низкое качество услуг в государственном секторе, пострадавшие от ВИЧ / СПИДа должны
переключиться на частные инициативы. которые поставляют антиретровирусные препараты (АРВ) по низкой цене
.
2. Правительство предоставляет бесплатные лекарства с 2004 года, и к настоящему моменту им воспользовались 35000 из
, хотя размер пострадавшего населения в 150 раз больше, чем
человек.
3. Недавние инициативы сетей и компаний, таких как AIDS Care Network, Emcure,
Reliance-Cipla-CII, приведут к доступности столь необходимых лекарств для более
пострадавших людей.
4. Но как это иронично, что мы должны столкнуться с постоянной нехваткой лекарств, когда
Индия является одним из крупнейших мировых поставщиков непатентованных лекарств в развивающийся мир
.
(1) JFIJ
(2) JIIJ
(3) IFIJ
(4) IFFJ
(5) JFII
Данные варианты требуют, чтобы вы оценили утверждение 1 как суждение или вывод.«Учитывая низкое качество услуг в государственном секторе…» — это скорее суждение, чем факт. Несмотря на то, что «низкое качество» услуг в публичном секторе нам известно, с одним и тем же мнением согласны не все. Даже я лично видел, что есть больницы государственного сектора, которые бесплатно предоставляют такие же услуги мирового класса бедным. На основании этого суждение «должно быть переключено…». тоже приговор. Помните, что вывод, сделанный на основании факта, — это умозаключение, но вывод, сделанный на основе суждения, все же суждение.Утверждение 1 — это суждение. Это исключает варианты 3 и 4.
Цифры в выписке 2 являются результатом прямой проверки. Отсюда легко убедиться, что утверждение 2 — факт. Это исключает вариант 2.
Оценивая варианты 1 и 5, оба из которых говорят, что утверждение 4 является выводом, теперь необходимо установить, является ли утверждение 5 выводом или суждением (согласно вариантам 1 и 5).
«… как это иронично…» не подтверждено и не подтверждено фактами. Утверждение 4 — это приговор.
Следовательно, правильный ответ — вариант 1.

Утверждение 3 является выводом, поскольку инициативы (что является фактом) приводят к доступности столь необходимых лекарств для большего числа пострадавших людей. (что является суждением)

Пример — 3

1. Согласно всем статистическим данным, Сарва Шикша Абхиян сумел идти в ногу со своими амбициозными целями.
2. Схема полуденного питания была значительным стимулом для бедных отправлять своих малышей в школу, тем самым устанавливая жизненно важную связь между здоровым телом и
здоровым духом.
3. Только около 13 миллионов детей в возрастной группе от 6 до 14 лет не посещают школу.
4. Универсализация начального образования должна быть предпосылкой для эволюции и развития нашей страны.
(1) IIFJ
(2) JIIJ
(3) IJFJ
(4) IJFI
(5) JIFI

Утверждение 1 является выводом. «По статистическим данным…» говорит нам, что все последующее основано на статистике, следовательно, на умозаключении. Это исключает варианты 2 и 5.
* В утверждении 2 (оценивается как суждение или вывод) «значительный стимул» — это суждение (насколько значительным можно проверить с помощью статистических данных, тогда это утверждение является выводом, а не фактом). «жизненно важная связь» между здоровым телом и здоровым разумом не может быть проверена. Следовательно, это суждение. Остается
вариантов 3 и 4. В вариантах указано, что предложение 3 является фактом. Предложение 4 должно оцениваться либо как вывод, либо как Суждение. «… Должно быть предпосылкой для эволюции….»Не может быть подтверждено на основании фактов, делающих приговор 4 приговором. Следовательно, правильный ответ — вариант 3.

Пример — 4

1. Мы не должны безнадежно увлекаться ошибочным убеждением, что коррупция в Индии вызвана коварством индейцев.
2. На самом деле у нас больше бюрократии: у нас уходит восемьдесят девять дней, чтобы открыть малый бизнес, у австралийцев — два.
3. Бюрократия ведет к коррупции и искажает характер народа.
4. Каждая бюрократическая процедура является точкой контакта с должностным лицом, и такие контакты
могут потенциально стать возможностью для получения денег, переходящих из рук в руки.
(1) JFIF
(2) JFJJ
(3) JIJF
(4) IFJF
(5) JFJI

Некоторые вещи делают утверждение 1 суждением — «не должно быть», «безнадежно зависимым», «ошибочным» , и «кривость индейцев»; Ни один из них не является фактом или подтверждением выводов.
Утверждение 2 представляет собой комбинацию вывода и фактов.«У нас больше бюрократии» — это предположение, но «правда в том» поясняет, что автор принимает это как должное, так как появляется больше бюрократии и сайтов, например «мы берем 89 дней и т. Д.», Что является фактом. Автор не делает вывод из статистического примера, но после подтверждения, что у нас есть еще болтовня, просто приводится пример. Поскольку суть утверждения основана на фактах, его следует классифицировать как факт. Поэтому варианты 3 и 4 исключены.
Варианты 1, 2 и 5 остаются. Утверждение 3 классифицируется как в вариантах 2, так и в вариантах 5 как суждение.и конечно это личное мнение. Искажение личного характера — мнение субъективное.
Утверждение 4 должно рассматриваться как суждение или вывод. Первая часть предложения 4 — факт. Во второй части «потенциал» определяется на основе фактов / опыта. Следовательно, это вывод. Это исключает варианты 1 и 2.
Следовательно, правильный ответ — вариант 5.

Пример — 5

1. Неравномерное распределение всех видов ресурсов, безусловно, является одним из самых сильных и зловещих. источники конфликта.
2. Мы знаем, что даже без войны конфликты продолжают нас беспокоить — они только меняют характер.
3. Полное разоружение — единственная гарантия нашего будущего; представьте себе количество ресурсов, которые можно высвободить и перераспределить.
4. Экономики промышленно развитого западного мира получают 20% своего дохода от
продажи всех видов оружия.

(1) IJJI
(2) JIJF
(3) IIJF
(4) JIIF
(5) JIF

Первое предложение должно оцениваться как суждение или вывод.«Самое зловещее» нельзя ни проверить, ни проверить. Очевидно, что это мнение, превращающее его в суждение. Это исключает варианты 1, 3 и 5.
Оценивая варианты 2 и 4, нужно решить, является ли утверждение 3 выводом или суждением. «Только страхование» не является ни подтвержденным фактом, ни поддающимся проверке заключением. Следовательно, это суждение, которое исключает вариант 4.

Утверждение 3 является умозаключением. Мы могли сказать «конфликты продолжают беспокоить нас» только исходя из нашего прошлого опыта.
Следовательно, правильный ответ — вариант 2.

4.3: Предложения, выводы и суждения

20 Предложения, выводы и суждения

³⁵

Рассмотрим следующие два утверждения:

— Она раздражает, но я люблю ее. — Я люблю ее, но она меня раздражает.

Что здесь говорится? С технической точки зрения, «но» действует как союз, и эти два предложения логически означают одно и то же. Они означают: «Я люблю ее, а она раздражает» и не более того. Иногда сложно уловить тонкости языка в логических системах, и это один из примеров.В первом случае упор делается на любовь, а во втором — на раздражение. Сегодняшний урок посвящен некоторым тонкостям языка и тому, как мы ежедневно понимаем логику на нашем обычном языке. Хотя предложение (утверждение, которое может быть истинным или ложным) говорит об одном технически, его значение на обычном языке значительно отличается. Суждения — это когда мы определяем, является ли утверждение истинным или ложным. Таким образом, определение Истины вышеупомянутого утверждения было бы одним делом в логике и другим в реальной жизни.Почему нас волнует Истина или Ложь утверждений? Потому что знание того, истинны они или ложны, позволяет нам выяснить, что еще мы знаем. Независимо от того, истинны они или ложны, существуют выводы (утверждения, которые обязательно следуют из предположения, что определенные утверждения истинны), которые мы можем понять. В целом процесс тот же: что еще мы можем сделать с учетом того, что нам сказали? Логическая эквивалентность означает, что два утверждения функционально эквивалентны Истине, что означает, что они оба Истинны при одинаковых обстоятельствах.По сути, это означает, что всякий раз, когда одно из них истинно, другое также истинно. Если мы сможем понять, какие утверждения логически эквивалентны, тогда мы сможем понять основную идею следствий. Отдельные утверждения могут дать нам некоторые выводы, такие как эквивалентность, и именно с этого мы начнем, прежде чем переходить к более сложным выводам в форме доказательств и выводов. А пока мы собираемся более подробно остановиться на дизъюнкциях, чтобы понять, что мы можем вывести из основных утверждений.

Исключительные и неисключительные дизъюнкции ³⁶

ПРИМЕЧАНИЕ: ∙ = & в тексте ниже. Существуют разные обозначения, и в некоторых из них используется символ ∙ для обозначения союзов.

Связки «или» и «либо… или» используются в повседневных беседах двумя разными способами. Когда ведущий спрашивает вас: «Кофе или чай?», Неявно подразумевается, что вы должны выбрать кофе или чай, но не оба сразу. Соединительное слово «или» используется в исключительном смысле для обозначения «одного или другого, но не обоих».После этого, когда ведущий снова спросит вас: «Сливки или сахар?», Вы можете ответить, сказав: «И то, и другое, пожалуйста». Теперь связка используется в неисключительном смысле «одно или другое, или оба».

Вот пример неисключительного употребления «либо… или…»:

Огонь или дым могут повредить картины.

F ∨ S

F: Огонь может повредить картины.

S: Дым может повредить картины.

Если огонь или дым сами по себе могут повредить картины, то оба вместе могут повредить картины.

В логике высказываний клин «∨» используется для обозначения неисключительных дизъюнкций. Таким образом, предложение обозначается как F ∨ S.

.

Напротив, в следующем предложении «либо… либо…» используется в исключительном смысле.

Федеральная резервная система либо повысит процентные ставки, либо оставит их нетронутыми.

∼ (R ∙ L)

R: Федеральная резервная система повысит процентные ставки.

L: Федеральная резервная система оставит процентные ставки нетронутыми.

∼ (R ∙ L). Первое соединение R ∨ L означает, что Федеральная резервная система сделает то или иное, либо и то, и другое. Но второй конъюнкт ∼ (R ∙ L) говорит, что Федеральная резервная система не будет делать и то, и другое. Таким образом, вместе они улавливают значение «одного или другого, но не обоих».

Как обозначить «если»

Составное предложение, образованное связкой «если», может быть обозначено как условное или двуконусное, в зависимости от значения предложения. Его также можно обозначить как дизъюнкцию.Но при этом нам нужно обратить внимание на то, является ли это исключительной или неисключительной дизъюнкцией. Приговор

Джефф не сможет получить высшее образование, если не выполнит все требования GE.

Мы также можем переписать это как

Джефф либо выполняет все требования GE, либо не может получить высшее образование.

∼G ∼G, потому что вполне возможно, что Джефф выполнил все требования GE, но все еще не может закончить обучение, например, из-за того, что он еще не выполнил требования к общему количеству единиц.∼G логически эквивалентно ∼G ∨ C. В результате мы можем обозначить его как ∼G ∨ C.

Джефф не сможет получить высшее образование, если не выполнит все требования GE.

∼G C

«Не… оба…» и «Оба… не…»

Важно не объединять «Не… оба…» и «Оба… не…». Сравните эти два предложения:

Моне и Шопен не являются художниками.

Дело не в том, что Моне — художник, а Шопен — художник.

∼ (M ∙ C)

М: Моне художник.

C: Шопен — художник.

И Дворжак, и Шуберт не художники.

Дворжак не художник, а Шуберт не художник.

∼S

D: Дворжак — художник.

S: Шуберт — художник.

Первое предложение отрицает, что и Моне, и Шопен — художники. То есть там сказано, что хоть один из них не художник. Его можно перефразировать как

.

Ни Моне, ни Шопен не художник.

Либо Моне не художник, либо Шопен не художник.

∼C ∼C, если полностью разложить его как

Либо Моне не художник, либо Шопен не художник.

∼C.

Напротив, второе предложение — союз.

И Дворжак, и Шуберт не художники.

Дворжак не художник, а Шуберт не художник.

∼S

D: Дворжак — художник.

S: Шуберт — художник.

Более того, это логически эквивалентно обоим предложениям ниже:

Ни Дворжак, ни Шуберт не художник.

Дело не в том, что Дворжак художник или Шуберт художник.

∼ (D ∨ S)

Ни Дворжак, ни Шуберт не художники.

Дело не в том, что Дворжак художник или Шуберт художник.

∼ (D ∨ S)

∼S логически эквивалентно ∼ (D ∨ S).

Следующие формулы суммируют различия между «Не… оба…» и «Оба… не…» и показывают, как их обозначать:

∼q ∼q = Ни p, ни q = ∼ (p ∨ q) = Ни p, ни q = ∼ (p ∨ q)

заключений и выводов | Колледж Куэста

Делать выводы и делать выводы

Прочтите с целью и смыслом.

Под выводом подразумевается информация, которая подразумевается или подразумевается. Это означает что информация никогда не указывается четко.

Писатели часто говорят вам больше, чем говорят прямо.Они дают вам подсказки или подсказки, которые помогут вам «прочитать между строк «. Используя эти подсказки, вы сможете глубже понять свой чтение называется , выводя . Когда вы выводите , вы выходите за пределы поверхностных деталей, чтобы увидеть другие значения, которые подсказывают детали. или означает (не указано). Когда значения слов не указаны четко в контексте в тексте они могут быть подразумеваемыми — то есть предполагаемыми или намекаемыми.Когда значения подразумеваются, вы можете вывести из .

Вывод — это просто громкое слово, которое означает вывод или суждение . Если вы делаете вывод, что что-то произошло, вы не видите, не слышите, не чувствуете, не обоняете и не попробовать настоящее событие. Но исходя из того, что вы знаете, имеет смысл думать, что у него есть случилось.Вы делаете выводы каждый день. В большинстве случаев вы делаете это, не задумываясь об этом. Предположим, вы сидите в машине, остановленной на красный сигнал светофора. Ты слышу визг покрышек, затем громкий треск и разбитое стекло. Вы, , ничего не видите, , но вы, , делаете вывод, что произошла автомобильная авария. Все мы знаем звуки визга шин и авария. Мы знаем, что эти звуки почти всегда означают автомобильную аварию.Но могла быть какая-то другая причина, а значит и другая. объяснение звуков. Возможно, это не случайность двух движущихся транспортных средств. Возможно, разгневанный водитель протаранил припаркованную машину. Или, может быть, кто-то играл звук автомобильной аварии из записи. Делать умозаключений означает выбирать наиболее вероятное объяснение из имеющихся фактов.

Есть несколько способов помочь вам сделать выводы из того, что может подразумевать автор. Ниже приведены описания различных способов помочь вам сделать вывод.

General Sense

Значение слова может подразумеваться из общего смысла его контекста, поскольку значение слова заключен в тюрьму подразумевается в следующем предложении:

Убийц обычно сажают в тюрьму на более длительные сроки, чем грабителей.

Вы можете сделать вывод о значении заключен в тюрьму , ответив на вопрос «Что обычно происходит с теми, кто признан виновным в убийстве или ограбление? »Что вы усмотрели в значении слова , заключенный, ?

Если вы ответили, что они заперты в тюрьме, тюрьме или пенитенциарном учреждении, вы правильно вывел значение заключенных .

Примеры

Когда значение слова не вытекает из общего смысла его контекста, оно можно понять из примеров.Например,

Те, кто любит ходить в клубы, ходить на вечеринки и часто приглашать друзей в их домов на обед общительных .

Вы можете вывести значение общительный , ответив на вопрос: «Какое слово или слова описывают людей, принадлежащих к клубам, много ходите на вечеринки и часто приглашаете друзей к себе домой на ужин? »Что? Вы угадали значение слова стадный ?

Если вы ответили социальный или что-то вроде: «люди, которым нравится общество других», вы правильно сделали вывод значение стад .

Антонимы и контрасты

Когда значение слова не подразумевается общим смыслом его контекста или В примерах это может подразумеваться антонимом или контрастирующей мыслью в контексте. Антонимы — слова, которые имеют противоположные значения, например, счастливый и грустный. Например,

Бен бесстрашен, но его брат робок .

Вы можете сделать вывод о значении робкого , ответив на вопрос: «Если Бен бесстрашен, а Джим сильно отличается от Бена. Что касается страха, то какое слово описывает Джима? »

Если вы ответили на такое слово, как робкий , или испуганный , или испуганный , вы угадали значение робкого .

Контраст в следующем предложении подразумевает значение доверия :

Папа поверил моей истории , но реакция мамы была полным недоверием.

Вы можете сделать вывод о значении доверия , ответив на вопрос: «Если реакция мамы была недоверием, а папа — недоверием». очень отличается от маминой, какова была реакция папы? »

Если вы ответили, что папа верил этой истории, вы правильно поняли значение слова доверие; значит вера .

Остерегайтесь того, что вы предполагаете!

Когда предложение содержит незнакомое слово, иногда можно вывести общее значение предложения без вывода точного значения неизвестного слово.Например,

Когда мы приглашаем Полсонов на обед, они никогда не приглашают нас к себе домой пообедать; однако, когда у нас на обед Брауны, они всегда отвечают .

Читая это предложение, некоторые студенты делают вывод, что Брауны более желательны для ужина. гости, чем Полсоны, не выводя точного значения , отвечают .Другие студенты приходят к выводу, что Брауны отличаются от Полсонов тем, что они что-то взамен, когда их приглашают на обед; эти студенты делают правильный вывод что ответить взаимностью означает «сделать что-то взамен».

Делая выводы (умозаключения), вы действительно добиваетесь окончательного смысл вещей — что важно, почему важно, как влияет одно событие другой, как одно событие приводит к другому.

Недостаточно просто получить факты при чтении.
Вы должны подумать о том, что эти факты значат для вас.

мысли | Британника

Элементы мысли

Широкое использование слов в мышлении («безмолвная речь») способствовало убеждению, особенно среди психологов-бихевиористов и необихевиористов, что думать означает соединять языковые элементы субголосом.Ранние эксперименты показали, что мышление обычно сопровождается электрической активностью в мышцах артикуляционных органов мыслителя (например, в горле). Благодаря более поздней работе с электромиографическим оборудованием стало очевидно, что мышечные явления не являются действительными проводниками мышления; они просто облегчают соответствующую деятельность мозга, когда интеллектуальная задача особенно сложна. Отождествление мышления с речью подверглось критике со стороны российского психолога Льва Семеновича Выготского и швейцарского психолога развития Жана Пиаже, которые наблюдали истоки человеческого мышления в общей способности детей объединять невербальные действия в эффективные и гибкие комбинации.Эти теоретики настаивали на том, что мышление и речь возникают независимо, хотя они признавали глубокую взаимозависимость этих функций.

Три ученых, придерживающихся разных подходов: русский физиолог XIX века Иван Михайлович Сеченов; американский основатель бихевиоризма Джон Б. Ватсон; и Пиаже — независимо пришли к выводу, что действия, которые служат элементами мышления, являются интернализированными или «дробными» версиями двигательных реакций. Другими словами, элементы считаются ослабленными или сокращенными вариантами нервно-мышечных процессов, которые, если бы они не подвергались частичному торможению, вызывали бы видимые движения тела.

Чувствительные инструменты действительно могут обнаруживать слабую активность в различных частях тела, кроме органов речи, например, в конечностях человека, когда движение мыслится или воображается, но не происходит на самом деле. Недавние исследования показывают существование желудочного «мозга», набора нейронных сетей в желудке. Такие открытия породили теории о том, что люди думают всем телом, а не только мозгом, или что, по словам американского психолога Б. Ф. Скиннера, «мысль — это просто поведение — словесное или невербальное, скрытое или явное. .”

Логическим результатом этих и подобных заявлений была точка зрения периферизма. В работе Уотсона и американского психолога Кларка Л. Халла очевидно, что мышление зависит от событий в мускулатуре: этих событий, известных как проприоцептивные импульсы (т. Е. Импульсы, возникающие в ответ на физическое положение, позу, равновесие или внутреннее состояние). состояние), влияют на последующие события в центральной нервной системе, которые, в конечном итоге, взаимодействуют с внешними стимулами и определяют дальнейшие действия.Однако есть свидетельства того, что мышлению не препятствует прием лекарств, подавляющих всю мышечную активность. Более того, такие исследователи, как американский психолог Карл С. Лэшли, указали, что мышление, как и другие более или менее квалифицированные действия, часто происходит так быстро, что не хватает времени для передачи импульсов из центральной нервной системы. систему к периферическому органу и обратно между последовательными шагами. Таким образом, централистский взгляд на то, что мышление состоит из событий, ограниченных мозгом (хотя часто сопровождаемых широко распространенной активностью в остальной части тела), получил распространение позже в 20 веке.Тем не менее, каждое из этих нейронных событий можно рассматривать как ответ (на внешний стимул или на более раннюю нейронно-опосредованную мысль или комбинацию мыслей), так и как стимул (вызывающий последующую мысль или двигательную реакцию).

Элементы мышления классифицируются как «символы» в соответствии с концепцией знакового процесса («семиотика»), которая выросла из работы философов (например, Чарльза Сандерса Пирса), лингвистов (например, CK Ogden и Ivor A. Ричардс) и психологов, специализирующихся на обучении (Э.г., Халл, Нил Э. Миллер, О. Хобарт Моурер и Чарльз Э. Осгуд). Суть этой концепции состоит в том, что стимулирующее событие x можно рассматривать как знак, представляющий (или «обозначающий») другое событие y , если x вызывает некоторые, но не все, поведения (как внешние, так и internal), который был бы вызван y , если бы он присутствовал. Когда стимул, который квалифицируется как знак, является результатом поведения организма, для которого он действует как знак, он называется «символом».«Реакции, вызывающие стимулы», которые, как говорят, формируют мыслительные процессы (например, когда человек думает о чем-то поесть), являются яркими примерами.

Этот подход, который предпочитают психологи в отношении стимула-реакции (S-R) или неоассоциативного течения, контрастирует с таковым из различных когнитивистских или неорационалистских теорий. Вместо того, чтобы рассматривать компоненты мышления как производные вербальных или невербальных двигательных действий (и, таким образом, подчиняться законам обучения и производительности, применимым к усвоенному поведению в целом), когнитивисты рассматривают компоненты мышления как уникальные центральные процессы, регулируемые принципами, которые свойственно им.Эти теоретики придают первостепенное значение так называемым структурам, в которых организованы «когнитивные» элементы, и они склонны видеть выводы, применения правил, репрезентации внешней реальности и другие составляющие мышления в действии даже в простейших формах усвоения знаний. поведение.

Школа гештальт-психологии считает, что составляющие мышления имеют по существу ту же природу, что и паттерны восприятия, которые нервная система конструирует из сенсорных возбуждений.После середины 20 века аналогии с компьютерными операциями приобрели широкое распространение; как следствие, мышление стало описываться в терминах хранения, поиска и передачи элементов информации. Рассматриваемая информация считалась свободно переводимой с одной «кодировки» на другую без ущерба для ее функций. Важнее всего было то, как были объединены события и какие другие комбинации могли произойти вместо этого.

Расшифровка фактов, выводов и суждений

Раздел «Факты, умозаключения и суждения» появился совершенно неожиданно в работе CAT 2006 года, застигнув многих студентов врасплох.Конечно, в те дни работа CAT была непредсказуемой, а таинственность делала решение экзамена еще более увлекательным. Хорошо, хватит ностальгии. Перейдем к определениям, не так ли?

Определения:

Факт : Это касается информации, которую можно легко проверить. Обычно они представлены в виде цифр, статистики и т. Д. Без какого-либо заключения. Таким образом, если утверждение легко проверить, его можно легко идентифицировать как факт.

Вывод : Это логический вывод, обычно основанный на фактах. Это выводы о неизвестном, сделанные на основе известного.

Заключение = Факт + Заключение, основанное на факте

Судебное решение : Судебное решение, как следует из названия, является выражением мнения. Мнения обычно подразумевают одобрение или неодобрение людей, ситуаций и т. Д.

Суждение очень похоже на умозаключения, и именно здесь кандидат CAT обычно делает ошибку, принимая одно за другое.Основное различие между ними состоит в том, что при умозаключении вывод обычно легко и логически выводится из факта. Это не так в судебном решении, которое больше основывается на мнении по факту.

Примеры:
Чтобы было понятнее, давайте перейдем к некоторым примерам. Вот один из CAT 2006:

Вопрос :
1. Согласно всем статистическим данным, Сарва Шикша Абхиян сумел идти в ногу со своими амбициозными целями.
2. Схема полуденного питания была значительным стимулом для бедных отправлять своих малышей в школу, тем самым устанавливая жизненно важную связь между здоровым телом и здоровым духом.
3. Только около 13 миллионов детей в возрастной группе от 6 до 14 лет не посещают школу.
4. Универсализация начального образования должна быть предпосылкой для эволюции и развития нашей страны.
(1) IIFJ (2) JIIJ (3) IJFJ (4) IJFI (5) JIFI

Решение :
Давайте рассмотрим каждое утверждение.
Первое утверждение является настолько очевидным выводом, насколько это возможно. Первая часть предложения, т. Е. «По всем статистическим данным», является фактом, на основании которого сделана вторая часть предложения.В этом заявлении говорится, что на основании фактов можно сделать вывод, что Сарва Шикша Абхиян сумел идти в ногу со своими амбициозными целями. Таким образом, это можно легко обозначить как умозаключение.
Второе утверждение является суждением, поскольку оно ясно указывает на одобрение схемы полуденного питания. Кроме того, это не похоже на какие-либо факты в заявлении. Следовательно, это можно обозначить как суждение.
Третье утверждение снова очевидно является фактом, поскольку это статистика, которую легко проверить.
Четвертое утверждение — это суждение, поскольку слова «должно быть предварительным условием» указывают на мнение о чем-либо.

Давайте посмотрим на другой вопрос из CAT 2006:

Вопрос :
1. Мы не должны безнадежно увлекаться ошибочным убеждением, что коррупция в Индии вызвана кривостью индейцев
2. На самом деле у нас больше бюрократии — у нас уходит восемьдесят девять дней, чтобы начать малый бизнес, австралийцы занимают два.
3. Бюрократия ведет к коррупции и искажает характер людей.
4. Каждая бюрократическая процедура является точкой контакта с должностным лицом, и такие контакты могут потенциально стать возможностью для получения денег, переходящих из рук в руки.
(1) JFIF (2) JFJJ (3) JIJF (4) IFJF (5) JFJI

Решение :
Первое утверждение — это суждение. Слова «мы не должны» ясно указывают на мнение человека.
Второе утверждение является фактом, поскольку все утверждение легко проверить.
Третье утверждение — снова приговор. Бюрократия, ведущая к коррупции, указывает на мнение, а не на каком-либо факте в заявлении.
Четвертое утверждение — это умозаключение. Первая часть утверждения — это проверяемая часть, а вторая часть утверждения является производной / выводимой из первой части.

Стратегия :
Простая стратегия решения вопросов FIJ выглядит следующим образом:

1) Найдите факты среди утверждений. Их легче всего найти. Убедитесь, что все утверждение должно быть проверено
2) Исключите варианты ответа, где найденное утверждение не является фактом
3) Определите простые выводы или суждения среди оставшихся предложений
4) Удалите варианты ответа снова на основе тех, которые не не подходит

Это самый простой и быстрый способ решения вопросов.

Резюме и ответ на текст Хаякавы | Феликс Лю

Люди склонны замечать тенденции в поведении других. Например, они ожидают, что преступники будут продолжать совершать злонамеренные действия, а мошенники — продолжать жульничать. Это прогнозы, которые мы делаем на основе их поведения. Эти прогнозы могут вызвать недопонимание, которое может испортить отношения. Выводы — это разумная форма логики, но она часто сочетается с быстрым суждением. Выводы не обязательно ошибочны; на самом деле, это один из самых распространенных методов, которые мы используем для оценки.В наши дни люди верят, что умозаключение и личное суждение кажутся фактическими и в некотором роде разумными. Однако иногда это может быть неточно, потому что люди обычно предвзяты. Они будут делать выводы о результатах, которые они хотят видеть, поэтому они будут пытаться убедить все больше и больше людей верить своим предсказаниям. С.И.Хаякава, профессор колледжа и сенатор Калифорнии в 20 веке, подробно останавливается на различиях между отчетами, выводами и суждениями, чтобы показать нам, как лучше всего делать выводы.В книге Language in Thought and Action (1993) автор С.И. Хаякава проводит различие между сообщениями, выводами и суждениями и связывает теории с реальной жизнью. Хаякава обращается к текущим проблемам в нашем хаотическом обществе, указывая на эти различные типы общения и взаимодействия между людьми, что доказывает, что мы можем легко попасть в неприятности, не осознавая основы общения.

Во-первых, отчет обычно является наиболее надежным видом связи.Причина в том, что отчеты поддаются проверке. Если мы не согласны с отчетом, мы всегда можем найти источники и при необходимости проверить статью. Пока предоставлены надлежащие ресурсы, отчет может быть проверен — или, если он неточен, он может быть признан недействительным. Всегда есть способ проверить отчеты, даже если они написаны в прошлом. Когда мы оглядываемся на прошлые исследования, мы можем изменить аналогичный эксперимент и получить результаты, которые могут быть такими же или разными. Например, если мы хотим убедиться, что эксперимент, представленный в химическом отчете, осуществим в реальной жизни, мы можем повторить эксперименты и увидеть результаты своими глазами.Самый очевидный результат — наблюдение. Люди хотят, чтобы правда предстала перед их глазами; следовательно, они смогут проверить это самостоятельно. С другой стороны, мы обычно предполагаем, что автор делает все возможное, чтобы рассказать нам как можно правдивее то, что он знает. Мы прогнозируем, что результаты отчета будут беспристрастными, поскольку автору необходимо включить доказательства в отчет, и эти доказательства обычно поддаются проверке. Однако результат может измениться из-за эмоций и интереса автора.Поскольку люди ожидают, что отчет заслуживает доверия, то, что кто-то представляет ложную информацию, как если бы она была проверена, глубоко предосудительно.

Во-вторых, вывод по определению — это утверждение о неизвестном, основанное на известном. Основное различие между выводом и отчетом состоит в том, что мы не можем доказать, что тенденция, которую мы предсказываем, будет иметь место в жизни. В частности, когда мы прогнозируем погоду на завтра, мы можем сказать, что из-за того, что стрекозы летают низко, облако густое, а муравьи часто передвигаются, высока вероятность того, что скоро нас ждет ливень.Однако это всего лишь предположение, основанное на тенденции, и мы не можем делать поспешных выводов, основанных только на прогнозе. Более того, одно дело не может охватить все случаи. Другими словами, выводы могут быть основаны только на общей тенденции, которая часто или всегда возникала в одной ситуации. В любом случае умозаключения — это утверждения о предмете, которые непосредственно не известны, сделанные на основе того, что было замечено. Например, если один студент украдет небольшую сумму денег, это не обязательно означает, что студент снова будет красть деньги.Это пример одного случая. С другой стороны, если тот же студент продолжает воровать деньги, это тенденция, из которой мы можем сделать вывод, что он может совершить следующее преступление. С другой стороны, многие также верят, что студент больше не станет воровать. Из этих примеров мы можем сказать, что делаем выводы на основе наших ценностей. Следовательно, мы можем быть предвзятыми в выводах.

В-третьих, решение без дополнительных доказательств часто бывает личным или всегда неофициальным. Суждение обычно исходит от внутреннего «я», которое обычно помогает человеку принимать решения.Согласно Хаякаве, «под суждениями мы будем иметь в виду выражения одобрения или неодобрения говорящим событий, лиц или объектов, которые он описывает» (25). В общем, суждение — это утверждение, которое требует дополнительных доказательств, подтверждающих, что это произойдет, или что это правда. Например, мы знаем, что «Трамп — плохой человек», это утверждение, в которое кто-то верит, и это тоже приговор; однако у этого нет никаких доказательств, подтверждающих этот аргумент. Это пример «скелета», которому нужны дополнительные доказательства в поддержку этого утверждения.Например, кто-то сказал бы, что Трамп негативно относится к гонке и относится к ней; Трамп публично насилует женщин; он беззастенчиво относится к гомосексуалистам. Это отчеты, подтверждающие суждение, и мы можем проверить утверждения и статистику в Интернете. С другой стороны, быстрое суждение тоже плохо, потому что останавливает мыслительный процесс. Суждение также является заключением, поскольку оно оценивает ряд ранее наблюдаемых фактов. Быстро оценивая его поведение, люди сделают вывод, что у этого человека нет хорошего руководства, которое не может принести пользу США, которые оценивают его возможности.

С. И. Хаякава помог нам лучше понять тот факт, что умозаключение плюс суждение никогда не могут равняться сообщению. Из-за неправильного понимания вывода многие люди испытывают трудности с взаимодействием из-за быстрых суждений. Он указал, что выводы не могут ничего убедительно доказать, потому что они основаны на предсказаниях и предположениях. Он также научил нас, что суждения могут отключать мыслительные способности людей. Самое главное, отчеты можно проверять; следовательно, они обычно заслуживают доверия.Читая этот отрывок, мы, наконец, получаем общее представление о поддержании отношений, которые мы никогда не хотим разрушать, потому что мы можем использовать язык ответственно. Будучи студентом, я всегда делаю много разных, не относящихся к делу сведений вместе, что в конечном итоге приводит к неверным выводам. Отрывок помогает мне лучше понять, как можно верить данным. Прочитав отрывок, он помог мне разобраться в различиях между ними, а также помочь мне лучше различать надежные источники и ненаучную логику, которая не может быть доказана.Зная различия, это помогает мне лучше понимать мир, и я могу получать более точные отчеты, которые я могу проверить, что может помочь мне продвинуться дальше в мире, который я хочу исследовать.

Цитирование

Хаякава С. И. и Алан Р. Хаякава. «Отчеты, заключения и суждения». В Язык в мысли и действии. Сан-Диего: Харкорт Брейс Йованович, 1993.

Логические аргументы

Аргументы и выводы

Дисциплина логики

Человеческая жизнь полна решений, включая значительный выбор того, во что верить.Хотя все предпочитают верить в то, что есть правда, мы часто не соглашаемся друг с другом по поводу того, что это такое в конкретных случаях. Может случиться так, что некоторые из наших самых фундаментальных жизненных убеждений приобретены случайным образом, а не с помощью разума, но все мы признаем, что наши убеждения в отношении самих себя и мира часто связаны во многих важных отношениях.

Если я верю, что киты — это млекопитающие, а все млекопитающие — рыбы, то для меня также имеет смысл верить, что киты — это рыбы.Даже тот, кто (справедливо!) Не соглашался с моим пониманием биологической систематики, мог оценить последовательный и разумный способ, которым я использовал свои ошибочные убеждения в качестве основы для создания нового. С другой стороны, если я решу поверить в то, что Гамлет был датским, потому что я считаю, что Гамлет был персонажем пьесы Шоу, а некоторые датчане — шавианскими персонажами, то даже тот, кто разделяет мою веру в результат, может указать, что я на самом деле не предоставили веских причин для признания своей истины.

В общем, мы можем уважать прямолинейность пути, даже если мы не принимаем точки, в которых он начинается и заканчивается. Таким образом, можно отличить правильное рассуждение от неправильного независимо от нашего согласия по вопросам существа. Логика — это дисциплина, которая изучает это различие — как путем определения условий, при которых истинность одних убеждений естественным образом приводит к истинности некоторых других убеждений, так и путем привлечения внимания к путям, которыми мы можем заставить нас поверить во что-либо без уважения к другим убеждениям. это правда.Это не дает гарантии, что мы всегда придем к истине, поскольку убеждения, с которых мы начинаем, иногда ошибочны. Но следование принципам правильного рассуждения действительно гарантирует, что в ходе нашего прогресса не будут закрадываться дополнительные ошибки.

В этом обзоре элементарной логики мы предпримем широкий обзор основных разновидностей рассуждений, которые были исследованы логиками западной философской традиции. Мы увидим, как одни модели мышления неизменно ведут от истины к истине, а другие — нет, и мы разовьем навыки использования первых, избегая при этом вторых.Будет полезно начать с определения некоторых технических терминов, которые описывают человеческое мышление в целом.

Структура аргумента

Наша основная единица того, что можно утверждать или отрицать, — это предложение (или заявление), который обычно выражается декларативным предложением. Логики ранних веков часто отождествляли предложения с мысленными актами их утверждения, которые часто назывались суждений, но мы можем избежать некоторых интересных, но острых философских вопросов, избегая этого выражения.

Предложения отличаются от предложений, которые их передают. «Смит любит Джонса» выражает то же самое суждение, что и «Смит любит Джонса», в то время как предложение «Сегодня у меня день рождения» можно использовать для передачи множества различных утверждений, в зависимости от того, кто это произносит и в какой день. Но каждое утверждение либо истинно, либо ложно. Иногда, конечно, мы не знаем, какое из этих истинностных значений имеет конкретное предложение (пример: «Есть жизнь на третьей луне Юпитера»), но мы можем быть уверены, что оно имеет то или иное значение. .

Основная задача логики состоит в том, как истинность одних предложений связана с истинностью других. Таким образом, мы обычно будем рассматривать группу связанных предложений. Аргумент — это набор из двух или более утверждений, связанных друг с другом таким образом, что все, кроме одного, (помещения) должны поддерживать оставшуюся (вывод). Переход или движение от посылок к заключению, логическая связь между ними и есть вывод, на котором основан аргумент.

Обратите внимание, что «посылка» и «вывод» здесь определены только в том смысле, в котором они встречаются по отношению друг к другу в рамках определенного аргумента. Одно и то же суждение может (и часто появляется) как вывод одной линии рассуждений, но также как одна из предпосылок другой. Ряд слов и фраз обычно используется в обычном языке для обозначения посылок и вывода аргумента, хотя их использование никогда строго не требуется, поскольку контекст может прояснить направление движения.Что отличает аргумент от простого набора предложений, так это вывод, который должен иметь место между ними.

Так, например, «Луна сделана из зеленого сыра, а клубника красная. У моей собаки блохи». это просто набор несвязанных предложений; правда или ложь каждого не имеет никакого отношения к другим. Но «Хелен — врач. Значит, Хелен ходила в медицинский институт, поскольку все врачи ходили в медицинский институт». это аргумент; истинность его вывода, «Хелен училась в медицинской школе», логически вытекает из его предпосылок: «Хелен — врач.»и« Все врачи учились в медицинской школе ».

Признание аргументов

Важно уметь определять, какое утверждение является выводом каждого аргумента, поскольку это необходимый шаг в нашей оценке вывода, который должен к нему привести. Мы могли бы даже использовать простую диаграмму для представления структуры аргумента, пронумеровав каждое из содержащихся в нем суждений и нарисовав стрелку, чтобы указать вывод, который ведет от его посылки (й) к его заключению.

Не волнуйтесь, если эта процедура поначалу покажется довольно предварительной и неуверенной. По мере продвижения мы будем изучать структурные особенности логических аргументов гораздо более подробно, и вскоре вы обнаружите, что легко обнаруживать экземпляры конкретных паттернов, с которыми мы сталкиваемся чаще всего. На данный момент достаточно указать разницу между аргументом и простым набором предложений и определить предполагаемый вывод каждого аргумента.

Даже это не всегда легко, поскольку аргументы, встроенные в обычный язык, могут принимать ошеломляющее разнообразие форм.Опять же, не беспокойтесь об этом слишком сильно; по мере того, как мы приобретаем более изощренные методы представления логических аргументов, мы намеренно ограничимся очень ограниченным числом различных паттернов и разработаем стандартные методы для выражения их структуры. Просто запомните основное определение аргумента: он включает более одного утверждения и выводит заключение из одной или нескольких предпосылок. Итак, «Если Джон уже ушел, значит, либо Джейн прибыла, либо Гейл уже в пути». не может быть аргументом, поскольку это всего лишь одно большое (составное) утверждение.Но «Джон уже ушел, так как Джейн приехала». это аргумент, который предлагает вывод из факта прибытия Джейн к заключению: «Джон уже уехал». Если вы сочтете полезным нарисовать диаграмму, воспользуйтесь этим методом в своих интересах.

---

Наша основная задача — оценить надежность умозаключений, моделей рассуждений, которые ведут от посылок к заключению в рамках логического аргумента. Мы уделим много внимания тому, что работает, а что нет.С самого начала жизненно важно различать два вида вывода, каждый из которых имеет свою отличительную структуру и критерий правильности.

Дедуктивные выводы

Когда аргумент утверждает, что истинность его посылок гарантирует истинность его вывода, говорят, что он включает дедуктивный вывод. Дедуктивное рассуждение соответствует очень высокому стандарту правильности. Дедуктивный вывод успешен только в том случае, если его посылки обеспечивают такую ​​абсолютную и полную поддержку его вывода, что было бы совершенно непоследовательно предполагать, что посылки истинны, а вывод ложен.

Обратите внимание, что каждый аргумент либо соответствует этому стандарту, либо нет; Там нет никакого среднего. Некоторые дедуктивные аргументы совершенны, и если их посылки на самом деле верны, то из этого следует, что их выводы также должны быть верными, независимо от того, что еще может случиться. Все остальные дедуктивные аргументы совершенно бесполезны — их выводы могут быть ложными, даже если их предпосылки верны, и никакая дополнительная информация не может им ни в малейшей степени помочь.

Индуктивные выводы

Когда аргумент утверждает, что истинность его посылок делает его вероятным или вероятным , что его вывод также является истинным, говорят, что он включает в себя индуктивный вывод.Стандарт правильности индуктивного рассуждения гораздо более гибок, чем критерий дедукции. Индуктивный аргумент оказывается успешным, когда его посылки дают некоторые законные основания. доказательства или подтверждение истинности его заключения. Хотя поэтому разумно признать истинность этого вывода на этих основаниях, не было бы совершенно непоследовательным отказать в суждении или даже полностью отрицать его.

Таким образом, индуктивные аргументы могут соответствовать своим стандартам в большей или меньшей степени, в зависимости от объема поддержки, которую они предоставляют.Никакой индуктивный аргумент не является ни абсолютно совершенным, ни полностью бесполезным, хотя можно сказать, что один относительно лучше или хуже другого в том смысле, что он рекомендует заключение с большей или меньшей степенью вероятности. В таких случаях соответствующая дополнительная информация часто влияет на надежность индуктивного аргумента, предоставляя другие доказательства, которые изменяют нашу оценку вероятности вывода.

Уже должна быть возможность различать аргументы этих двух типов с некоторой точностью.Помните, что дедуктивные аргументы претендуют на то, чтобы гарантировать свои выводы, в то время как индуктивные аргументы просто рекомендуют свои. Или спросите себя, может ли введение какой-либо дополнительной информации — за исключением изменения или отрицания каких-либо предпосылок — сделать вывод более или менее вероятным; если так, то рассуждение носит индуктивный характер.

Истина и действительность

Поскольку дедуктивное рассуждение требует такой прочной связи между предпосылками и заключением, мы проведем большую часть этого обзора, изучая различные модели дедуктивного вывода.Поэтому стоит рассмотреть критерий правильности дедуктивных аргументов более подробно.

Дедуктивный аргумент называется действительно, когда вывод от посылок к заключению безупречен. Вот два эквивалентных способа сформулировать этот стандарт:

• Если предпосылки действительного аргумента верны, то его вывод также должен быть верным.
• Невозможно, чтобы вывод действительного аргумента был ложным, пока его посылки истинны.

(Рассматривая посылки как набор предложений, мы будем говорить, что посылки истинны только в тех случаях, когда истинно каждое из этих предложений.) Любой неверный дедуктивный аргумент является недействительный: его вывод может быть ложным, в то время как его посылки истинны, поэтому, даже если посылки истинны, заключение может оказаться либо истинным, либо ложным.

Обратите внимание, что действительность вывода дедуктивного аргумента не зависит от истинности его посылок; должны быть выполнены оба условия , чтобы быть уверенным в истинности заключения.Из восьми различных возможных комбинаций истины и достоверности полностью исключена только одна:

Помещения	Заключение	Заключение
Верно	Действительно	Верно
		ХХХХ
	Неверно	Верно
		Ложь
Неверно	Действительно	Верно
		Ложь
	Неверно	Верно
		Ложь

Единственное, чего не может случиться, — это чтобы дедуктивный аргумент имел истинные посылки и действительный вывод, но ложный вывод.